八年级数学上册人教版 12.2.1直角三角形全等的判定 试题(含答案)
文档属性
| 名称 | 八年级数学上册人教版 12.2.1直角三角形全等的判定 试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 181.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 20:14:37 | ||
图片预览


文档简介
12.2.1直角三角形全等的判定
一.选择题
1.下列条件中,不能判定两个直角三角形全等的是( )
A.两个锐角对应相等
B.两条直角边对应相等
C.一个锐角和斜边对应相等
D.斜边和一条直角边对应相等
2.下列条件,不能判定两个直角三角形全等的是( )
A.两个锐角对应相等
B.一个锐角和斜边对应相等
C.两条直角边对应相等
D.一条直角边和斜边对应相等
3.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,添加一个条件,不能使得Rt△ABC≌Rt△DCB的是( )
A.AB=DC B.AC=DB C.∠ABC=∠DCB D.BC=BD
4.如图,已知AB⊥BD,CD⊥BD,若用“HL”判定Rt△ABD和Rt△CDB全等,则需要添加的条件是( )
A.AD=CB B.∠A=∠C C.BD=DB D.AB=CD
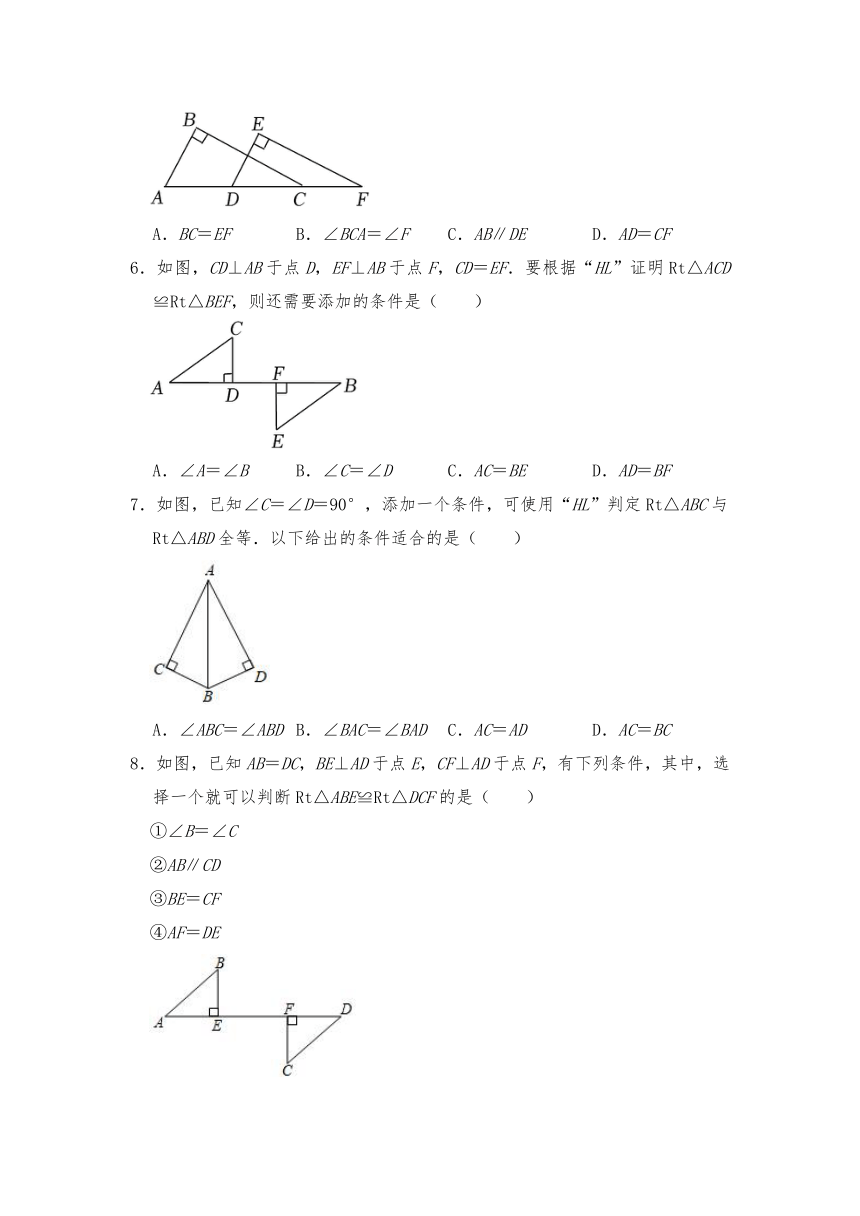
5.如图,已知点A、D、C、F在同一条直线上,∠B=∠E=90°,AB=DE,若添加一个条件后,能用“HL”的方法判定Rt△ABC≌Rt△DEF,添加的条件可以是( )
A.BC=EF B.∠BCA=∠F C.AB∥DE D.AD=CF
6.如图,CD⊥AB于点D,EF⊥AB于点F,CD=EF.要根据“HL”证明Rt△ACD≌Rt△BEF,则还需要添加的条件是( )
A.∠A=∠B B.∠C=∠D C.AC=BE D.AD=BF
7.如图,已知∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.∠ABC=∠ABD B.∠BAC=∠BAD C.AC=AD D.AC=BC
8.如图,已知AB=DC,BE⊥AD于点E,CF⊥AD于点F,有下列条件,其中,选择一个就可以判断Rt△ABE≌Rt△DCF的是( )
①∠B=∠C
②AB∥CD
③BE=CF
④AF=DE
A.①② B.①②③ C.①③④ D.①②③④
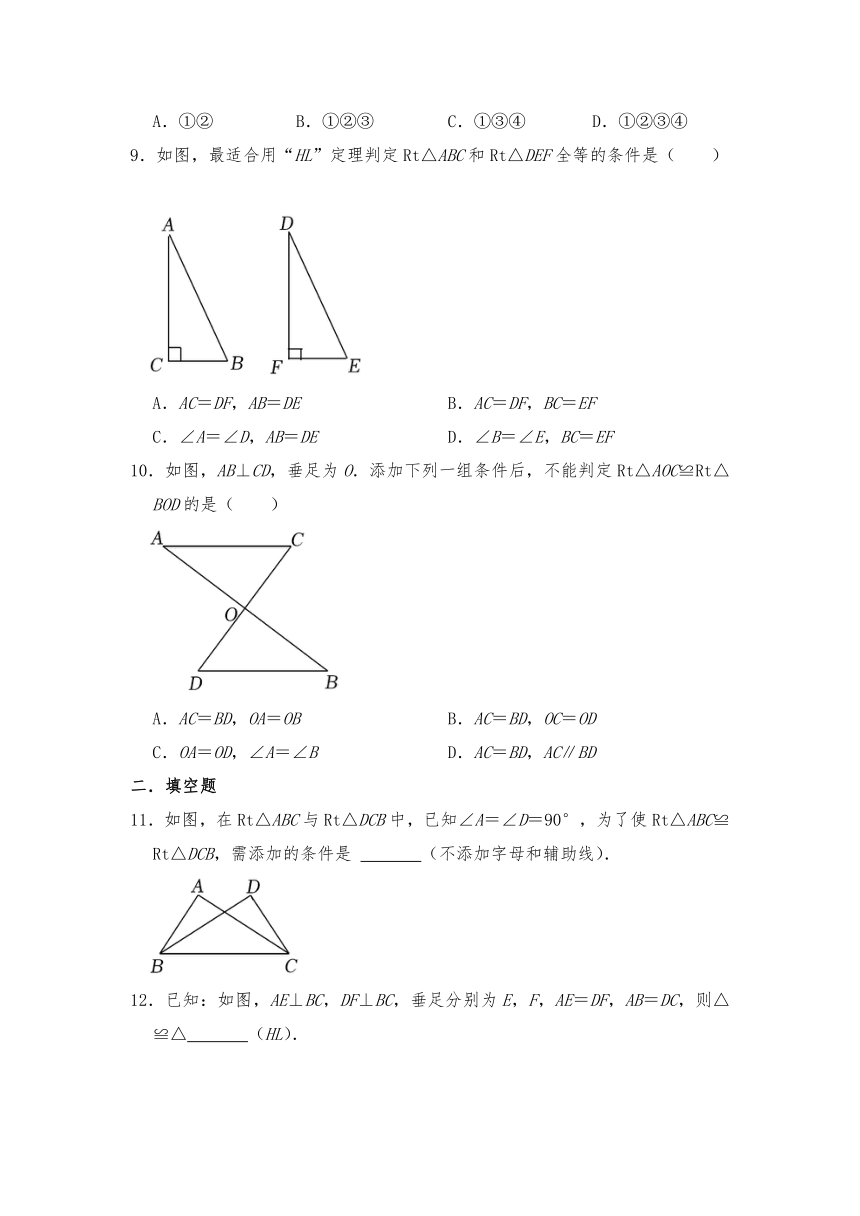
9.如图,最适合用“HL”定理判定Rt△ABC和Rt△DEF全等的条件是( )
A.AC=DF,AB=DE B.AC=DF,BC=EF
C.∠A=∠D,AB=DE D.∠B=∠E,BC=EF
10.如图,AB⊥CD,垂足为O.添加下列一组条件后,不能判定Rt△AOC≌Rt△BOD的是( )
A.AC=BD,OA=OB B.AC=BD,OC=OD
C.OA=OD,∠A=∠B D.AC=BD,AC∥BD
二.填空题
11.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,为了使Rt△ABC≌Rt△DCB,需添加的条件是 (不添加字母和辅助线).
已知:如图,AE⊥BC,DF⊥BC,垂足分别为E,F,AE=DF,AB=DC,则△ ≌△ (HL).
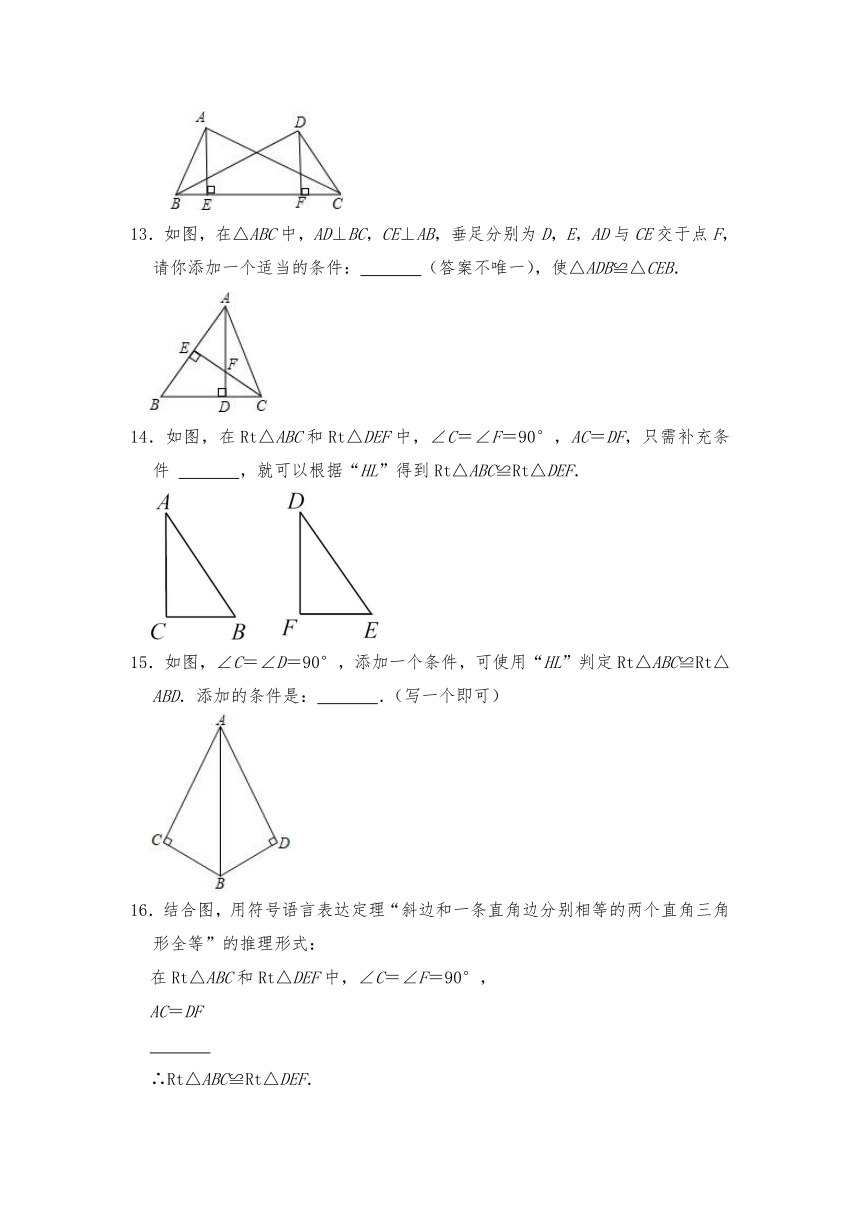
13.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE交于点F,请你添加一个适当的条件: (答案不唯一),使△ADB≌△CEB.
14.如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=DF,只需补充条件 ,就可以根据“HL”得到Rt△ABC≌Rt△DEF.
15.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC≌Rt△ABD.添加的条件是: .(写一个即可)
16.结合图,用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式:
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
AC=DF
∴Rt△ABC≌Rt△DEF.
三.解答题
17.如图,△ABC的高BD与CE相交于点O,OD=OE,AO的延长线交BC于点M,请你从图中找出几对全等的直角三角形,并说明理由.
18.在四边形ABCD中,∠ABC=∠ADC=90°,BE⊥AC于E,DF⊥AC于F,CF=AE,BC=DA.求证:Rt△ABE≌Rt△CDF.
19.如图,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2.
20.如图,点C、E、B、F在一条直线上,AB⊥CF于B,DE⊥CF于E,AC=DF,AB=DE.求证:CE=BF.
21.证明命题:“一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小颖根据题意画出的图形,并写出了不完整的已知和求证.
已知:在 Rt△ABC和 Rt△A'B'C'中,∠C=∠C'=90°,AC=A'C',AD与A'D'分别为BC,B'C'边上的中线且 .
求证: .
请补全已知和求证部分,并写出证明过程.
22.如图,AB=BC,∠BAD=∠BCD=90°,点D是EF上一点,AE⊥EF于E,CF⊥EF于F,AE=CF,连接BD,求证:Rt△ADE≌Rt△CDF.
答案
一.选择题
A.A.D.A.D.C.C.D.A.C.
二.填空题
11.AB=DC(答案不唯一).
12.ABE;DCF.
13.AB=BC.
14.AB=DE.
15.AC=AD(答案不唯一).
16.AB=DE.
三.解答题
17.△ADO≌△AEO,△DOC≌△EOB,△COM≌△BOM,△ACM≌△ABM,△ADB≌△AEC,△BCE≌△CBD.理由如下:
在△ADO与△AEO中,∠ADO=∠AEO=90°,
,
∴△ADO≌△AEO(HL),
∴∠DAO=∠EAO,AD=AE.
在△DOC与△EOB中,
,
∴△DOC≌△EOB(ASA),
∴DC=EB,OC=OB,
∴DC+AD=EB+AE,即AC=AB,
∵∠DAO=∠EAO,
∴AM⊥BC,CM=BM.
在△COM与△BOM中,∠OMC=∠OMB=90°,
,
∴△COM≌△BOM(HL).
在△ACM与△ABM中,∠AMC=∠AMB=90°,
,
∴△ACM≌△ABM(HL).
在△ADB与△AEC中,
,
∴△ADB≌△AEC(SAS).
在△BCE与△CBD中,∠BEC=∠CDB=90°,
,
∴△BCE≌△CBD(HL).
18.如图,
在Rt△ADC与Rt△CBA中,
,
∴Rt△ADC≌Rt△CBA(HL),
∴DC=BA.
又∵BE⊥AC于E,DF⊥AC于F,
∴∠AEB=∠CFD=90°,
在Rt△ABE与Rt△CDF中,
,
∴Rt△ABE≌Rt△CDF(HL).
19.证明:∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
∴△ABC与△ACD为直角三角形,
在Rt△ABC和Rt△ADC中,
∵AB=AD,AC为公共边,
∴Rt△ABC≌Rt△ADC(HL),
∴∠1=∠2.
20.证明:∵AB⊥CF,DE⊥CF,
∴∠ABC=∠DEF=90°.
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL).
∴BC=EF.
∴BC﹣BE=EF﹣BE.
即:CE=BF.
21.AD=A'D';Rt△ABC≌Rt△A'B'C'(写成△ABC≌△A'B'C'也对);
证明:∵∠C=∠C'=90°,AD=A'D',AC=A'C',
∴Rt△ADC≌Rt△A'D'C'(HL),
∴CD=C'D'.
∵AD与A'D'分别为BC与B'C'边上的中线,
∴点D和点D'分别是BC与B'C'的中点,
∴BC=2CD,B'C'=2C'D',
∴BC=B'C',
在△ABC和△A'B'C'中,
,
∴Rt△ABC≌Rt△A'B'C'(SAS).
22.证明:∵∠BAD=∠BCD=90°,
在Rt△ABD和Rt△CBD中,
,
∴Rt△ABD≌Rt△CBD(HL),
∴AD=CD,
∵AE⊥EF于E,CF⊥EF于F,
∴∠E=∠F=90°,
在Rt△ADE和Rt△CDF中,
,
∴Rt△ADE≌Rt△CDF(HL)
一.选择题
1.下列条件中,不能判定两个直角三角形全等的是( )
A.两个锐角对应相等
B.两条直角边对应相等
C.一个锐角和斜边对应相等
D.斜边和一条直角边对应相等
2.下列条件,不能判定两个直角三角形全等的是( )
A.两个锐角对应相等
B.一个锐角和斜边对应相等
C.两条直角边对应相等
D.一条直角边和斜边对应相等
3.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,添加一个条件,不能使得Rt△ABC≌Rt△DCB的是( )
A.AB=DC B.AC=DB C.∠ABC=∠DCB D.BC=BD
4.如图,已知AB⊥BD,CD⊥BD,若用“HL”判定Rt△ABD和Rt△CDB全等,则需要添加的条件是( )
A.AD=CB B.∠A=∠C C.BD=DB D.AB=CD
5.如图,已知点A、D、C、F在同一条直线上,∠B=∠E=90°,AB=DE,若添加一个条件后,能用“HL”的方法判定Rt△ABC≌Rt△DEF,添加的条件可以是( )
A.BC=EF B.∠BCA=∠F C.AB∥DE D.AD=CF
6.如图,CD⊥AB于点D,EF⊥AB于点F,CD=EF.要根据“HL”证明Rt△ACD≌Rt△BEF,则还需要添加的条件是( )
A.∠A=∠B B.∠C=∠D C.AC=BE D.AD=BF
7.如图,已知∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.∠ABC=∠ABD B.∠BAC=∠BAD C.AC=AD D.AC=BC
8.如图,已知AB=DC,BE⊥AD于点E,CF⊥AD于点F,有下列条件,其中,选择一个就可以判断Rt△ABE≌Rt△DCF的是( )
①∠B=∠C
②AB∥CD
③BE=CF
④AF=DE
A.①② B.①②③ C.①③④ D.①②③④
9.如图,最适合用“HL”定理判定Rt△ABC和Rt△DEF全等的条件是( )
A.AC=DF,AB=DE B.AC=DF,BC=EF
C.∠A=∠D,AB=DE D.∠B=∠E,BC=EF
10.如图,AB⊥CD,垂足为O.添加下列一组条件后,不能判定Rt△AOC≌Rt△BOD的是( )
A.AC=BD,OA=OB B.AC=BD,OC=OD
C.OA=OD,∠A=∠B D.AC=BD,AC∥BD
二.填空题
11.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,为了使Rt△ABC≌Rt△DCB,需添加的条件是 (不添加字母和辅助线).
已知:如图,AE⊥BC,DF⊥BC,垂足分别为E,F,AE=DF,AB=DC,则△ ≌△ (HL).
13.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE交于点F,请你添加一个适当的条件: (答案不唯一),使△ADB≌△CEB.
14.如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=DF,只需补充条件 ,就可以根据“HL”得到Rt△ABC≌Rt△DEF.
15.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC≌Rt△ABD.添加的条件是: .(写一个即可)
16.结合图,用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式:
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
AC=DF
∴Rt△ABC≌Rt△DEF.
三.解答题
17.如图,△ABC的高BD与CE相交于点O,OD=OE,AO的延长线交BC于点M,请你从图中找出几对全等的直角三角形,并说明理由.
18.在四边形ABCD中,∠ABC=∠ADC=90°,BE⊥AC于E,DF⊥AC于F,CF=AE,BC=DA.求证:Rt△ABE≌Rt△CDF.
19.如图,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2.
20.如图,点C、E、B、F在一条直线上,AB⊥CF于B,DE⊥CF于E,AC=DF,AB=DE.求证:CE=BF.
21.证明命题:“一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小颖根据题意画出的图形,并写出了不完整的已知和求证.
已知:在 Rt△ABC和 Rt△A'B'C'中,∠C=∠C'=90°,AC=A'C',AD与A'D'分别为BC,B'C'边上的中线且 .
求证: .
请补全已知和求证部分,并写出证明过程.
22.如图,AB=BC,∠BAD=∠BCD=90°,点D是EF上一点,AE⊥EF于E,CF⊥EF于F,AE=CF,连接BD,求证:Rt△ADE≌Rt△CDF.
答案
一.选择题
A.A.D.A.D.C.C.D.A.C.
二.填空题
11.AB=DC(答案不唯一).
12.ABE;DCF.
13.AB=BC.
14.AB=DE.
15.AC=AD(答案不唯一).
16.AB=DE.
三.解答题
17.△ADO≌△AEO,△DOC≌△EOB,△COM≌△BOM,△ACM≌△ABM,△ADB≌△AEC,△BCE≌△CBD.理由如下:
在△ADO与△AEO中,∠ADO=∠AEO=90°,
,
∴△ADO≌△AEO(HL),
∴∠DAO=∠EAO,AD=AE.
在△DOC与△EOB中,
,
∴△DOC≌△EOB(ASA),
∴DC=EB,OC=OB,
∴DC+AD=EB+AE,即AC=AB,
∵∠DAO=∠EAO,
∴AM⊥BC,CM=BM.
在△COM与△BOM中,∠OMC=∠OMB=90°,
,
∴△COM≌△BOM(HL).
在△ACM与△ABM中,∠AMC=∠AMB=90°,
,
∴△ACM≌△ABM(HL).
在△ADB与△AEC中,
,
∴△ADB≌△AEC(SAS).
在△BCE与△CBD中,∠BEC=∠CDB=90°,
,
∴△BCE≌△CBD(HL).
18.如图,
在Rt△ADC与Rt△CBA中,
,
∴Rt△ADC≌Rt△CBA(HL),
∴DC=BA.
又∵BE⊥AC于E,DF⊥AC于F,
∴∠AEB=∠CFD=90°,
在Rt△ABE与Rt△CDF中,
,
∴Rt△ABE≌Rt△CDF(HL).
19.证明:∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
∴△ABC与△ACD为直角三角形,
在Rt△ABC和Rt△ADC中,
∵AB=AD,AC为公共边,
∴Rt△ABC≌Rt△ADC(HL),
∴∠1=∠2.
20.证明:∵AB⊥CF,DE⊥CF,
∴∠ABC=∠DEF=90°.
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL).
∴BC=EF.
∴BC﹣BE=EF﹣BE.
即:CE=BF.
21.AD=A'D';Rt△ABC≌Rt△A'B'C'(写成△ABC≌△A'B'C'也对);
证明:∵∠C=∠C'=90°,AD=A'D',AC=A'C',
∴Rt△ADC≌Rt△A'D'C'(HL),
∴CD=C'D'.
∵AD与A'D'分别为BC与B'C'边上的中线,
∴点D和点D'分别是BC与B'C'的中点,
∴BC=2CD,B'C'=2C'D',
∴BC=B'C',
在△ABC和△A'B'C'中,
,
∴Rt△ABC≌Rt△A'B'C'(SAS).
22.证明:∵∠BAD=∠BCD=90°,
在Rt△ABD和Rt△CBD中,
,
∴Rt△ABD≌Rt△CBD(HL),
∴AD=CD,
∵AE⊥EF于E,CF⊥EF于F,
∴∠E=∠F=90°,
在Rt△ADE和Rt△CDF中,
,
∴Rt△ADE≌Rt△CDF(HL)
