八年级数学上册人教版 12.2.2全等三角形的应用 试题(含答案)
文档属性
| 名称 | 八年级数学上册人教版 12.2.2全等三角形的应用 试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 332.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 20:21:05 | ||
图片预览



文档简介
12.2.2全等三角形的应用
一.选择题
1.如图,把两根钢条AB,CD的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).只要量得AC的长度,就可知工件的内径BD是否符合标准,这是利用的什么数学原理呢?( )
A.SSS B.SAS C.ASA D.AAS
2.如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为△ABC,提供下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A.AB,BC,CA B.AB,BC,∠B C.AB,AC,∠B D.∠A,∠B,BC
3.如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,发现DE=AB.那么判定△ABC和△DEC全等的依据是( )
A.SSS B.SAS C.ASA D.AAS
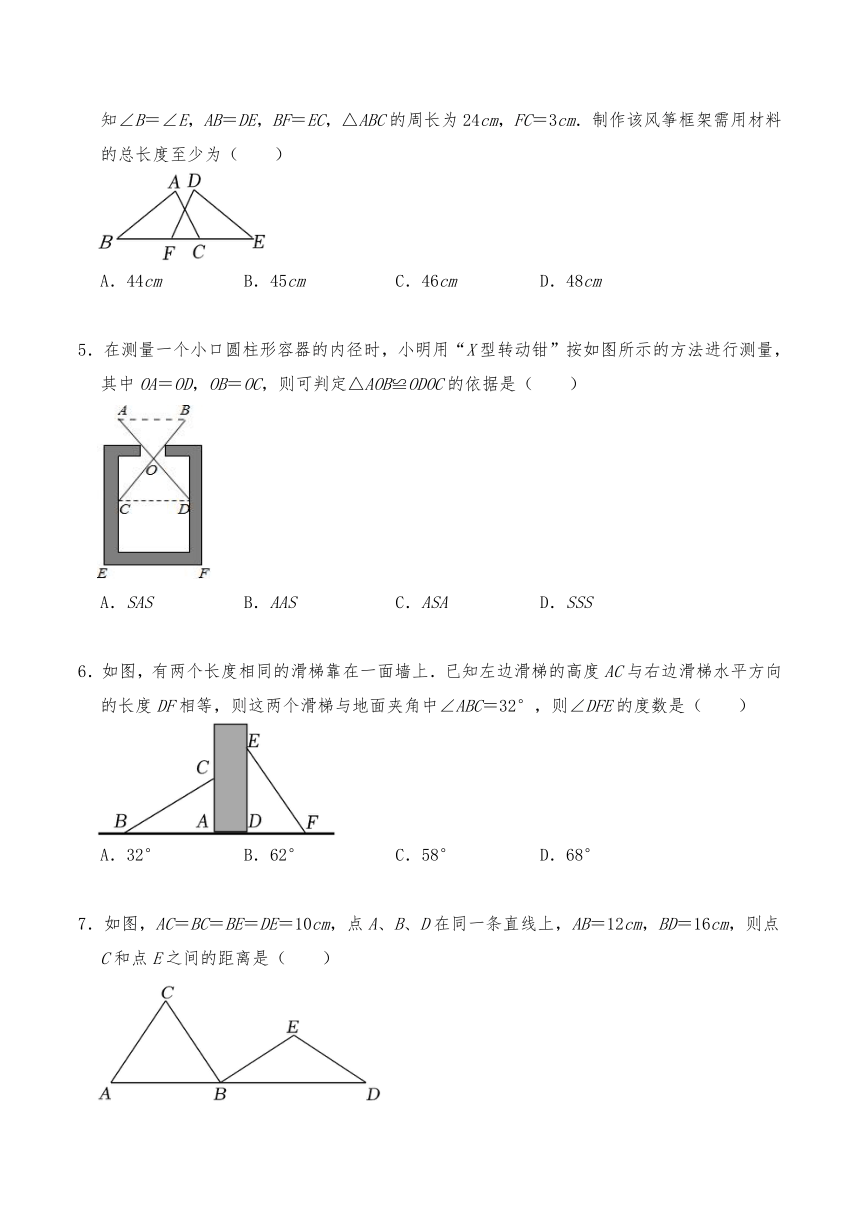
4.“又是一年三月三”.在校内劳动课上,小明所在小组的同学们设计了如图所示的风筝框架.已知∠B=∠E,AB=DE,BF=EC,△ABC的周长为24cm,FC=3cm.制作该风筝框架需用材料的总长度至少为( )
A.44cm B.45cm C.46cm D.48cm
5.在测量一个小口圆柱形容器的内径时,小明用“X型转动钳”按如图所示的方法进行测量,其中OA=OD,OB=OC,则可判定△AOB≌ODOC的依据是( )
A.SAS B.AAS C.ASA D.SSS
6.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角中∠ABC=32°,则∠DFE的度数是( )
A.32° B.62° C.58° D.68°
7.如图,AC=BC=BE=DE=10cm,点A、B、D在同一条直线上,AB=12cm,BD=16cm,则点C和点E之间的距离是( )
A.6cm B.7cm C.8cm D.
8.一块三角形玻璃不慎被小明摔成了四片碎片(如图所示),小明经过仔细的考虑认为只要带其中的两块碎片去玻璃店,就可以让师傅配一块与原玻璃一样的玻璃.你认为下列四个答案中考虑最全面的是( )
A.带其中的任意两块去都可以
B.带1、4或2、3去就可以了
C.带1、4或3、4去就可以了
D.带1、2或2、4去就可以了
9.如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄A和C,A和D间也有公路相连,且公路AD是南北走向,AC=3km,只有A和B之间由于间隔了一个小湖,无直接相连的公路.现决定在湖面上造一座桥,测得AE=1.2km,BF=0.7km,则建造的桥长至少为( )
A.1.2km B.1.1km C.1km D.0.7km
10.如图,要测量河两岸相对的A、B两点的距离,可以在与AB垂直的河岸BF上取C、D两点,且使BC=CD,从点D出发沿与河岸BF的垂直方向移动到点E,使点E与A,C在一条直线上,可得△ABC≌△EDC,这时测得DE的长就是AB的长.判定△ABC≌△EDC最直接的依据是( )
A.ASA B.HL C.SAS D.SSS
二.填空题
11.如图,小明想测量池塘两端A,B间的距离,为了安全起见,小明借助全等三角形的知识,用了这样一个间接测量A,B间的距离方法:在地上取一点可以直接到达A点和B点的点C,测得AC长20m,BC长为20m,在AC的延长线上找一点D,使得CD长为20m,在BC的延长线上找一点E,使得CE长为20m,又测得此时D和E的距离为25m,根据小明的数据,可知A,B之间的距离为 m.
12.如图,黄芳不小心把一块三角形的玻璃打成三块碎片,现要带其中一块去配出与原来完全一样的玻璃,正确的办法是带来第 块去配.
13.如图,小刚站在河边的A点处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树C处,接着再向前走了30步到达D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他一共走了140步.如果小刚一步大约50厘米,估计小刚在点A处时他与电线塔的距离为 .
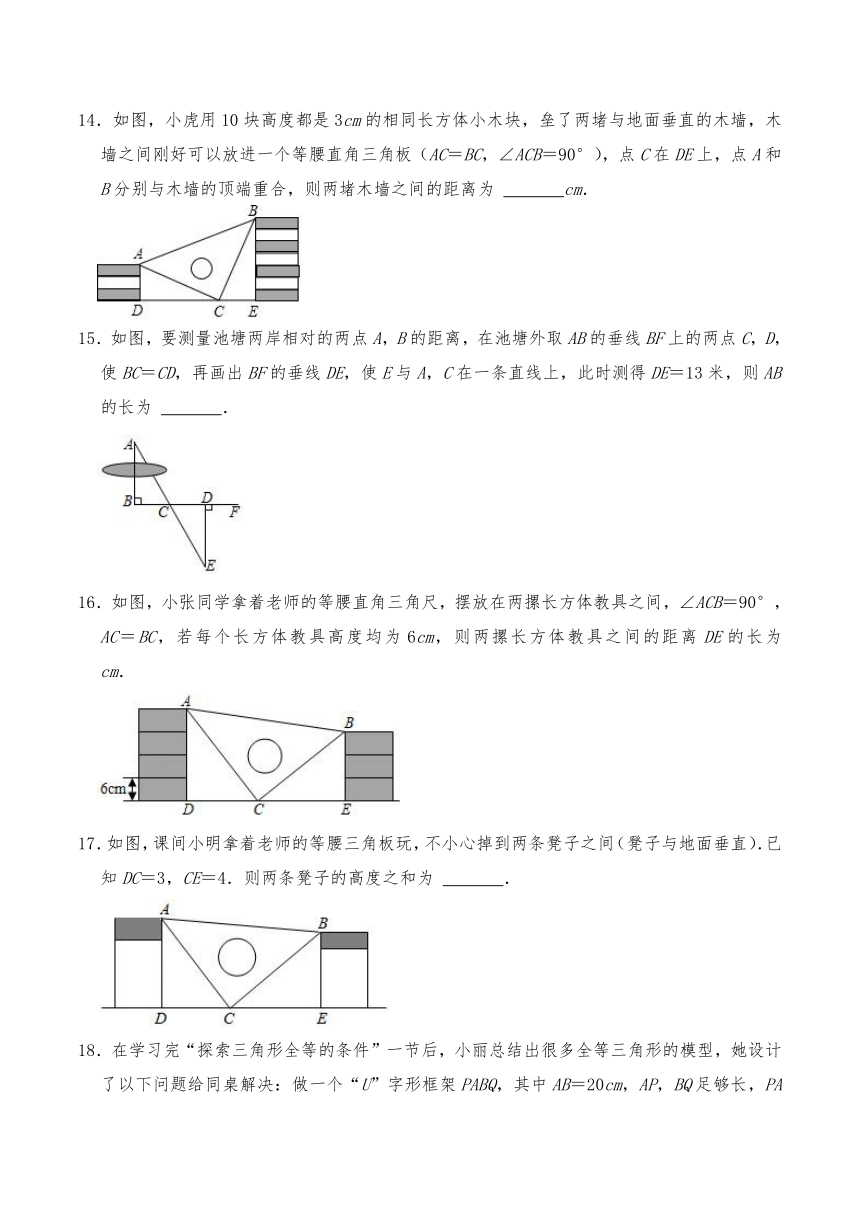
14.如图,小虎用10块高度都是3cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
15.如图,要测量池塘两岸相对的两点A,B的距离,在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,此时测得DE=13米,则AB的长为 .
16.如图,小张同学拿着老师的等腰直角三角尺,摆放在两摞长方体教具之间,∠ACB=90°,AC=BC,若每个长方体教具高度均为6cm,则两摞长方体教具之间的距离DE的长为 cm.
17.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=3,CE=4.则两条凳子的高度之和为 .
18.在学习完“探索三角形全等的条件”一节后,小丽总结出很多全等三角形的模型,她设计了以下问题给同桌解决:做一个“U”字形框架PABQ,其中AB=20cm,AP,BQ足够长,PA⊥AB于点A,QB⊥AB于点B,点M从B出发向A运动,点N从B出发向Q运动,速度之比为2:3,运动到某一瞬间两点同时停止,在AP上取点C,使△ACM与△BMN全等,则AC的长度为 cm.
三.解答题
19.某中学七年级同学到野外开展数学综合实践活动,在营地看到一个池塘,同学们想知道池塘两端(A、B为池塘的两端)的距离.有一位同学设计了如下测量方案:先在平地上取一个可直接到达A、B的点E,连接AE、BE,分别延长AE至点D,延长BE至点C,使得ED=AE,EC=BE,若测出CD的长为18m,求这个池塘两端AB的长,并说明理由.
20.如图,某广场有一座雕塑,A,B两点分别位于底座两端,但利用现有的皮尺无法直接得到A,B两点间的距离,请你设计一个方案,测出A、B两点间的距离,并说明理由.
21.如图,有一池塘,要测池塘两端A,B的距离,先在平地上取一个点C,从点C不经过池塘直接到达点A和B;再连接AC,BC并分别延长到点D,E,使CD=CA,CE=CB;连接DE.求证DE=AB.
22.如图,小明和小华住在同一个小区不同单元楼,他们想要测量小明家所在单元楼AB的高度,首先他们在两栋单元楼之间选定一点E,然后小华在自己家阳台C处测得E处的俯角为∠1,小明站在E处测得眼睛F到AB楼端点A的仰角为∠2,发现∠1与∠2互余,已知EF=1米,BE=CD=20米,BD=58米,试求单元楼AB的高.
23.小琪同学在数学实践活动课上,老师要求她利用所学几何知识测量出学校门前小河的宽度(即图中AB的长),经过思考探究,小琪设计方案如下:
如图,先测量出BE=DE,∠B=∠D=90°,点B、E、D在同一直线上,点A,E,C在同一直线上,测量出CD=8m,小琪就知道河面宽度AB的长了.则你认为河宽AB是多少?请说明理由.
24.如图,A,B两点位于高墙外,不能直接到达.为在该高楼的楼顶上搭建一个支架,需要在地面测量出A,B间的距离.学习了三角形全等知识后,小明给出了如下的方案:先在地面上取一点可以直接到达A点和B点的点O,连接AO并延长到C,使OC=OA;连接BO并延长到D,使OD=OB,连接CD并测量出CD的长度,CD的长度就是A,B间的距离.请根据以上的信息,说明AB=CD.
答案
一.选择题
B.C.B.B.A.C.D.C.B.A.
二.填空题
11.25.
12.③.
13.40米.
14.30.
15.13米.
16.42.
17.7.
18.8或15.
三.解答题
19.在△AEB和△DEC中,
,
∴△AEB≌△DEC(SAS);
∴AB=CD(全等三角形的对应边相等).
∵CD=10m,
∴AB=10m,
答:池塘两端的距离是10米.
20.在地面选择一点O,连接AO并延长至点C,使OC=OA,延长BO至点D,使OD=OB,
测量CD的长,即为A、B两点间的距离,
理由如下:在△AOB和△COD中,
,
∴△AOB≌△COD(SAS),
∴AB=CD.
21.证明:由题意知CD=CA,CE=CB,
在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),
∴DE=AB.
22.过F作FG⊥AB于G,
则四边形BEFG是矩形,
∴FG=BE=20米,BG=EF=1米,
∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
在△AFG与△ECD中,
,
∴△AFG≌△ECD(ASA),
∴AG=DE=BD﹣BE=38(米),
∴AB=AG+BG=38+1=39(米),
答:单元楼AB的高为39米.
23.河宽为8米,理由如下:
在△ABE和△CDE中,
.
∴△ABE≌△CDE(ASA).
∴AB=CD=8m.
24.在△AOB与△COD中,
,
则△AOB≌△COD(SAS).
所以AB=CD.
一.选择题
1.如图,把两根钢条AB,CD的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).只要量得AC的长度,就可知工件的内径BD是否符合标准,这是利用的什么数学原理呢?( )
A.SSS B.SAS C.ASA D.AAS
2.如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为△ABC,提供下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A.AB,BC,CA B.AB,BC,∠B C.AB,AC,∠B D.∠A,∠B,BC
3.如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,发现DE=AB.那么判定△ABC和△DEC全等的依据是( )
A.SSS B.SAS C.ASA D.AAS
4.“又是一年三月三”.在校内劳动课上,小明所在小组的同学们设计了如图所示的风筝框架.已知∠B=∠E,AB=DE,BF=EC,△ABC的周长为24cm,FC=3cm.制作该风筝框架需用材料的总长度至少为( )
A.44cm B.45cm C.46cm D.48cm
5.在测量一个小口圆柱形容器的内径时,小明用“X型转动钳”按如图所示的方法进行测量,其中OA=OD,OB=OC,则可判定△AOB≌ODOC的依据是( )
A.SAS B.AAS C.ASA D.SSS
6.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角中∠ABC=32°,则∠DFE的度数是( )
A.32° B.62° C.58° D.68°
7.如图,AC=BC=BE=DE=10cm,点A、B、D在同一条直线上,AB=12cm,BD=16cm,则点C和点E之间的距离是( )
A.6cm B.7cm C.8cm D.
8.一块三角形玻璃不慎被小明摔成了四片碎片(如图所示),小明经过仔细的考虑认为只要带其中的两块碎片去玻璃店,就可以让师傅配一块与原玻璃一样的玻璃.你认为下列四个答案中考虑最全面的是( )
A.带其中的任意两块去都可以
B.带1、4或2、3去就可以了
C.带1、4或3、4去就可以了
D.带1、2或2、4去就可以了
9.如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄A和C,A和D间也有公路相连,且公路AD是南北走向,AC=3km,只有A和B之间由于间隔了一个小湖,无直接相连的公路.现决定在湖面上造一座桥,测得AE=1.2km,BF=0.7km,则建造的桥长至少为( )
A.1.2km B.1.1km C.1km D.0.7km
10.如图,要测量河两岸相对的A、B两点的距离,可以在与AB垂直的河岸BF上取C、D两点,且使BC=CD,从点D出发沿与河岸BF的垂直方向移动到点E,使点E与A,C在一条直线上,可得△ABC≌△EDC,这时测得DE的长就是AB的长.判定△ABC≌△EDC最直接的依据是( )
A.ASA B.HL C.SAS D.SSS
二.填空题
11.如图,小明想测量池塘两端A,B间的距离,为了安全起见,小明借助全等三角形的知识,用了这样一个间接测量A,B间的距离方法:在地上取一点可以直接到达A点和B点的点C,测得AC长20m,BC长为20m,在AC的延长线上找一点D,使得CD长为20m,在BC的延长线上找一点E,使得CE长为20m,又测得此时D和E的距离为25m,根据小明的数据,可知A,B之间的距离为 m.
12.如图,黄芳不小心把一块三角形的玻璃打成三块碎片,现要带其中一块去配出与原来完全一样的玻璃,正确的办法是带来第 块去配.
13.如图,小刚站在河边的A点处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树C处,接着再向前走了30步到达D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他一共走了140步.如果小刚一步大约50厘米,估计小刚在点A处时他与电线塔的距离为 .
14.如图,小虎用10块高度都是3cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
15.如图,要测量池塘两岸相对的两点A,B的距离,在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,此时测得DE=13米,则AB的长为 .
16.如图,小张同学拿着老师的等腰直角三角尺,摆放在两摞长方体教具之间,∠ACB=90°,AC=BC,若每个长方体教具高度均为6cm,则两摞长方体教具之间的距离DE的长为 cm.
17.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=3,CE=4.则两条凳子的高度之和为 .
18.在学习完“探索三角形全等的条件”一节后,小丽总结出很多全等三角形的模型,她设计了以下问题给同桌解决:做一个“U”字形框架PABQ,其中AB=20cm,AP,BQ足够长,PA⊥AB于点A,QB⊥AB于点B,点M从B出发向A运动,点N从B出发向Q运动,速度之比为2:3,运动到某一瞬间两点同时停止,在AP上取点C,使△ACM与△BMN全等,则AC的长度为 cm.
三.解答题
19.某中学七年级同学到野外开展数学综合实践活动,在营地看到一个池塘,同学们想知道池塘两端(A、B为池塘的两端)的距离.有一位同学设计了如下测量方案:先在平地上取一个可直接到达A、B的点E,连接AE、BE,分别延长AE至点D,延长BE至点C,使得ED=AE,EC=BE,若测出CD的长为18m,求这个池塘两端AB的长,并说明理由.
20.如图,某广场有一座雕塑,A,B两点分别位于底座两端,但利用现有的皮尺无法直接得到A,B两点间的距离,请你设计一个方案,测出A、B两点间的距离,并说明理由.
21.如图,有一池塘,要测池塘两端A,B的距离,先在平地上取一个点C,从点C不经过池塘直接到达点A和B;再连接AC,BC并分别延长到点D,E,使CD=CA,CE=CB;连接DE.求证DE=AB.
22.如图,小明和小华住在同一个小区不同单元楼,他们想要测量小明家所在单元楼AB的高度,首先他们在两栋单元楼之间选定一点E,然后小华在自己家阳台C处测得E处的俯角为∠1,小明站在E处测得眼睛F到AB楼端点A的仰角为∠2,发现∠1与∠2互余,已知EF=1米,BE=CD=20米,BD=58米,试求单元楼AB的高.
23.小琪同学在数学实践活动课上,老师要求她利用所学几何知识测量出学校门前小河的宽度(即图中AB的长),经过思考探究,小琪设计方案如下:
如图,先测量出BE=DE,∠B=∠D=90°,点B、E、D在同一直线上,点A,E,C在同一直线上,测量出CD=8m,小琪就知道河面宽度AB的长了.则你认为河宽AB是多少?请说明理由.
24.如图,A,B两点位于高墙外,不能直接到达.为在该高楼的楼顶上搭建一个支架,需要在地面测量出A,B间的距离.学习了三角形全等知识后,小明给出了如下的方案:先在地面上取一点可以直接到达A点和B点的点O,连接AO并延长到C,使OC=OA;连接BO并延长到D,使OD=OB,连接CD并测量出CD的长度,CD的长度就是A,B间的距离.请根据以上的信息,说明AB=CD.
答案
一.选择题
B.C.B.B.A.C.D.C.B.A.
二.填空题
11.25.
12.③.
13.40米.
14.30.
15.13米.
16.42.
17.7.
18.8或15.
三.解答题
19.在△AEB和△DEC中,
,
∴△AEB≌△DEC(SAS);
∴AB=CD(全等三角形的对应边相等).
∵CD=10m,
∴AB=10m,
答:池塘两端的距离是10米.
20.在地面选择一点O,连接AO并延长至点C,使OC=OA,延长BO至点D,使OD=OB,
测量CD的长,即为A、B两点间的距离,
理由如下:在△AOB和△COD中,
,
∴△AOB≌△COD(SAS),
∴AB=CD.
21.证明:由题意知CD=CA,CE=CB,
在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),
∴DE=AB.
22.过F作FG⊥AB于G,
则四边形BEFG是矩形,
∴FG=BE=20米,BG=EF=1米,
∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
在△AFG与△ECD中,
,
∴△AFG≌△ECD(ASA),
∴AG=DE=BD﹣BE=38(米),
∴AB=AG+BG=38+1=39(米),
答:单元楼AB的高为39米.
23.河宽为8米,理由如下:
在△ABE和△CDE中,
.
∴△ABE≌△CDE(ASA).
∴AB=CD=8m.
24.在△AOB与△COD中,
,
则△AOB≌△COD(SAS).
所以AB=CD.
