八年级数学上册人教版 12.3角的平分线的性质 试题(含答案)
文档属性
| 名称 | 八年级数学上册人教版 12.3角的平分线的性质 试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 334.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 20:22:58 | ||
图片预览



文档简介
12.3角的平分线的性质
一.选择题
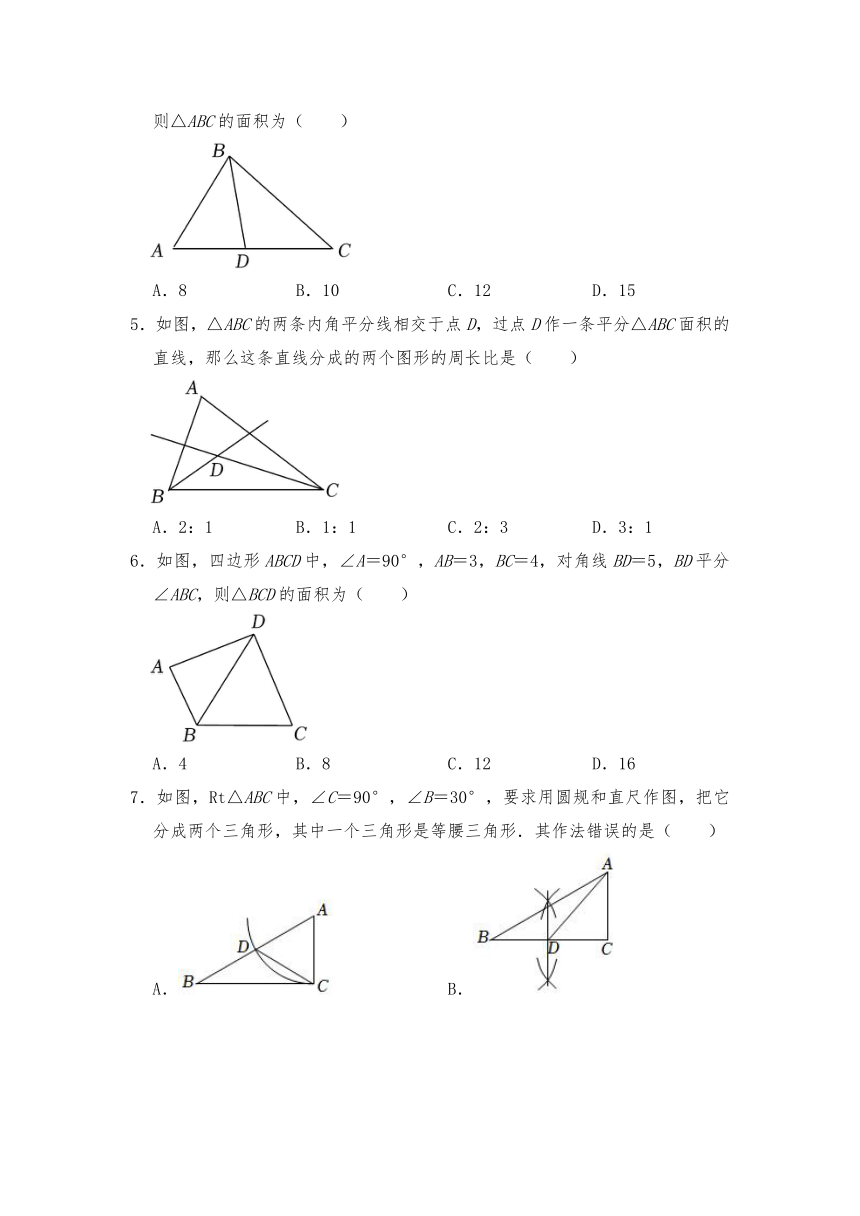
1.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=4,则PQ的长不可能是( )
A.3.5 B.4 C.4.5 D.5
2.如图,点P在∠AOB的角平分线上,过点P作PC⊥OA,交OA于点C,且PC=8,则P到OB的距离为( )
A.4 B.6 C.8 D.10
3.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,若AB=20,△ABD的面积为60,则CD长( )
A.12 B.10 C.6 D.4
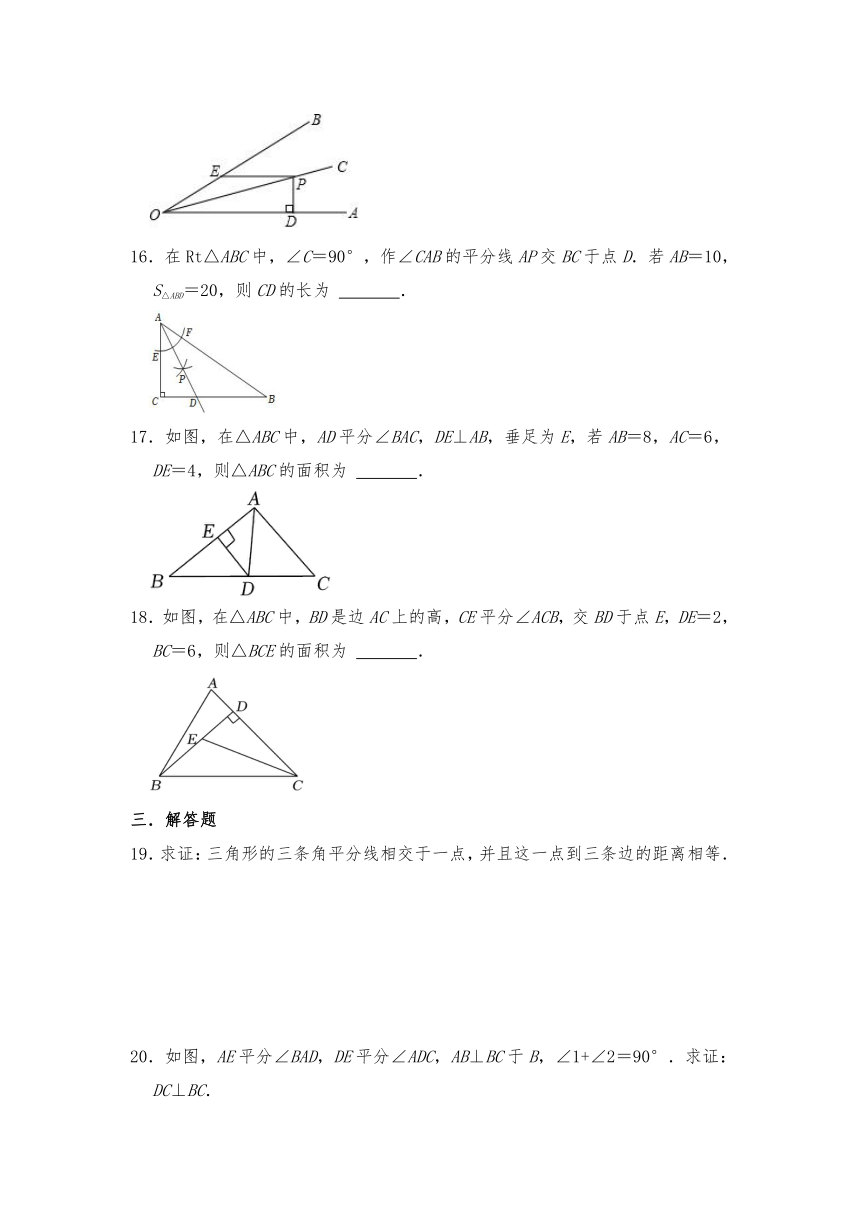
4.如图,在△ABC中,BD平分∠ABC,如果AB=4,BC=6,△ABD的面积为6,则△ABC的面积为( )
A.8 B.10 C.12 D.15
5.如图,△ABC的两条内角平分线相交于点D,过点D作一条平分△ABC面积的直线,那么这条直线分成的两个图形的周长比是( )
A.2:1 B.1:1 C.2:3 D.3:1
6.如图,四边形ABCD中,∠A=90°,AB=3,BC=4,对角线BD=5,BD平分∠ABC,则△BCD的面积为( )
A.4 B.8 C.12 D.16
7.如图,Rt△ABC中,∠C=90°,∠B=30°,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是( )
A. B.
C. D.
8.如图,一把直尺压住射线OB,另一把完全一样的直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”这样说的依据是( )
A.角平分线上的点到这个角两边的距离相等
B.三角形三条角平分线的交点到三条边的距离相等
C.在一个角的内部,到角的两边距离相等的点在这个角的平分线上
D.以上均不正确
9.如图,在△ABC中,∠C=90°,AC=3,BC=4,AD是∠CAB的平分线,设△ACD,△ABD的面积分别是S1,S2,则S1:S2等于( )
A.3:4 B.4:5 C.3:7 D.3:5
10.如图,点I是△ABC三条角平分线的交点,△ABI的面积记为S1,△ACI的面积记为S2,△BCI的面积记为S3,关于S1+S2与S3的大小关系,正确的是( )
A.S1+S2=S3 B.S1+S2<S3 C.S1+S2>S3 D.无法确定
二.填空题
11.如图,点C在∠AOB的平分线上,CD⊥OA于点D,且CD=3,如果E是射线OB上一点,那么线段CE长度的最小值是 .
12.如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= .
13.如图,△ABC的三边AB,BC,CA的长分别是100,110,120,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BOC:S△CAO= .
14.如图,△ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,如果AC=6cm,BC=8cm,则DE的长为 cm.
15.如图,OC平分∠AOB,点P在OC上,PD⊥OA于D,PD=6cm,点E是射线OB上的动点,则PE的最小值为 cm.
16.在Rt△ABC中,∠C=90°,作∠CAB的平分线AP交BC于点D.若AB=10,S△ABD=20,则CD的长为 .
17.如图,在△ABC中,AD平分∠BAC,DE⊥AB,垂足为E,若AB=8,AC=6,DE=4,则△ABC的面积为 .
18.如图,在△ABC中,BD是边AC上的高,CE平分∠ACB,交BD于点E,DE=2,BC=6,则△BCE的面积为 .
三.解答题
19.求证:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
20.如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,∠1+∠2=90°.求证:DC⊥BC.
21.如图,在△ABC中,∠C=90°.
(1)过点B作∠ABC的平分线交AC于点D(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);
(2)若CD=3,AB+BC=16,求△ABC的面积.
22.如图,在△ABC中,∠ABC=60°,∠ACB=40°,点P为∠ABC、∠ACB的角平分线的交点.
(1)∠BPC的度数是 .
(2)请问点P是否在∠BAC的角平分线上?请说明理由.
(3)证明:AB=PC.
23.数学学习不仅要理解概念的本质,而且还要记忆相关的结论,这样我们才能明白数学问题的意义,才能有数学的意识解决数学实际问题.
(1)叙述角平分线性质定理: ;
(2)叙述并证明角平分线性质定理的逆定理.
24.我们已经学习过角平分线性质定理,即:角平分线上的点到角两边的距离相等.
如图,已知△ABC的角平分线BD交边AC于点D.
(1)求证:=;
(2)求证:=;
(3)如果BC=4,AB=6,AC=5,那么CD= .
答案
一.选择题
A.C.C.D.B.B.B.C.D.C.
二.填空题
11.3.
12.1.
13.10:11:12.
14.3.
15.6.
16.4.
17.28.
18.6.
三.解答题
19.证明:如图,在△ABC中,角平分线BM与角平分线CN相交于点P,过点P分别作AB,BC,AC的垂线,垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,且PD⊥AB,PE⊥BC,垂足分别为D,E,
∴PD=PE(角平分线上的点到这个角的两边的距离相等).
同理,PE=PF.
∴PD=PE=PF.
∴点P在∠A的平分线上(在一个角的内部,到角的两边距离相等的点在这个角的平分线上),
即∠A的平分线经过点P.
故三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
20.证明:∵AE平分∠BAD,DE平分∠ADC,
∴∠1=∠3,∠2=∠4,
∵AB⊥BC,∠1+∠2=90°,
∴∠ABE=90°,∠AED=90°,∠4+∠1=90°,
∴∠3+∠6=90°,∠6+∠5=90°,
∴∠3=∠5,
∴∠4+∠5=90°,
∴∠DCE=180°﹣∠4﹣∠5=90°,
∴DC⊥BC.
21.(1)∠ABC的平分线如图所示.
(2)作DH⊥AB于H.
∵BD平分∠ABC,DC⊥BC,DH⊥AB,
∴CD=DH=3,
∴△ABC的面积=S△BCD+S△ABD=BC CD+AB DH=×3BC+3AB=(BC+AB)=3×16=24.
22.(1)∵P点是∠ABC和∠ACB角平分线的交点,
∴∠CBP=∠ABP=∠ABC,∠BCP=∠ACP=∠ACB,
∵∠ABC=60°,∠ACB=40°,
∴∠PBC+∠PCB=∠ABC+∠ACB=30°+20°=50°,
∴∠BPC=180°﹣50°=130°,
故答案为:130°;
(2)答:点P在∠BAC的角平分线上,理由如下:
过点p分别作三角形三边的垂线,垂足分别为D、E、F,
∵PB、PC分别是∠ABC、∠ACB 的角平分线,
∴PD=PE PE=PF,
∴PD=PF,
∴点P在∠BAC的角平分线上;
(3)证明:延长AP,在AP延长线上取PG=PC,连接GC,
∵AP、CP分别为∠BAC、∠ACB的平分线,
∴∠PAC=40°,∠ACP=20°,
∴∠GPC=∠PAC+∠ACP=60°,
∴△PGC为等边三角形,
∴∠G=60°=∠ABC,PC=CG,
在△ABC和△CGA中,
,
∴△ABC≌△CGA(AAS),
∴AB=CG,
又∵PC=CG,
故AB=PC.
23.(1)角平分线性质定理:角平分线上的任意一点,到角两边的距离相等.
故答案为:角平分线上的任意一点,到角两边的距离相等;
(2)角平分线性质定理的逆定理:到角的两边的距离相等的点在这个角的平分线上;
已知:如图,点P在∠AOB的内部,PC⊥OA,PD⊥OB,垂足分别为C、D,且PC=PD.
求证:点P在∠AOB的平分线上,
证明:如图,
∵PC⊥OA,PD⊥OB,
∴∠PCO=∠PDO=90°,
在Rt△PCO和Rt△PDO中,
,
∴Rt△PCO≌Rt△PDO(HL),
∴∠POC=∠POD,
∴OP是∠AOB的平分线,
即点P在∠AOB的平分线上.
24.(1)证明:作DF⊥BC于F点,作DH⊥AB于H点,如图,
∵BD是△ABC的角平分线,
∴DF=DH,
∴==;
(2)证明:作BE⊥CA于E点,如图,
∵==,
∵=;
∴=;
(3)解:∵=,
∴==,
∴=,即=,
∴CD=AC=×5=2.
故答案为:2.
一.选择题
1.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=4,则PQ的长不可能是( )
A.3.5 B.4 C.4.5 D.5
2.如图,点P在∠AOB的角平分线上,过点P作PC⊥OA,交OA于点C,且PC=8,则P到OB的距离为( )
A.4 B.6 C.8 D.10
3.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,若AB=20,△ABD的面积为60,则CD长( )
A.12 B.10 C.6 D.4
4.如图,在△ABC中,BD平分∠ABC,如果AB=4,BC=6,△ABD的面积为6,则△ABC的面积为( )
A.8 B.10 C.12 D.15
5.如图,△ABC的两条内角平分线相交于点D,过点D作一条平分△ABC面积的直线,那么这条直线分成的两个图形的周长比是( )
A.2:1 B.1:1 C.2:3 D.3:1
6.如图,四边形ABCD中,∠A=90°,AB=3,BC=4,对角线BD=5,BD平分∠ABC,则△BCD的面积为( )
A.4 B.8 C.12 D.16
7.如图,Rt△ABC中,∠C=90°,∠B=30°,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是( )
A. B.
C. D.
8.如图,一把直尺压住射线OB,另一把完全一样的直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”这样说的依据是( )
A.角平分线上的点到这个角两边的距离相等
B.三角形三条角平分线的交点到三条边的距离相等
C.在一个角的内部,到角的两边距离相等的点在这个角的平分线上
D.以上均不正确
9.如图,在△ABC中,∠C=90°,AC=3,BC=4,AD是∠CAB的平分线,设△ACD,△ABD的面积分别是S1,S2,则S1:S2等于( )
A.3:4 B.4:5 C.3:7 D.3:5
10.如图,点I是△ABC三条角平分线的交点,△ABI的面积记为S1,△ACI的面积记为S2,△BCI的面积记为S3,关于S1+S2与S3的大小关系,正确的是( )
A.S1+S2=S3 B.S1+S2<S3 C.S1+S2>S3 D.无法确定
二.填空题
11.如图,点C在∠AOB的平分线上,CD⊥OA于点D,且CD=3,如果E是射线OB上一点,那么线段CE长度的最小值是 .
12.如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= .
13.如图,△ABC的三边AB,BC,CA的长分别是100,110,120,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BOC:S△CAO= .
14.如图,△ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,如果AC=6cm,BC=8cm,则DE的长为 cm.
15.如图,OC平分∠AOB,点P在OC上,PD⊥OA于D,PD=6cm,点E是射线OB上的动点,则PE的最小值为 cm.
16.在Rt△ABC中,∠C=90°,作∠CAB的平分线AP交BC于点D.若AB=10,S△ABD=20,则CD的长为 .
17.如图,在△ABC中,AD平分∠BAC,DE⊥AB,垂足为E,若AB=8,AC=6,DE=4,则△ABC的面积为 .
18.如图,在△ABC中,BD是边AC上的高,CE平分∠ACB,交BD于点E,DE=2,BC=6,则△BCE的面积为 .
三.解答题
19.求证:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
20.如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,∠1+∠2=90°.求证:DC⊥BC.
21.如图,在△ABC中,∠C=90°.
(1)过点B作∠ABC的平分线交AC于点D(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);
(2)若CD=3,AB+BC=16,求△ABC的面积.
22.如图,在△ABC中,∠ABC=60°,∠ACB=40°,点P为∠ABC、∠ACB的角平分线的交点.
(1)∠BPC的度数是 .
(2)请问点P是否在∠BAC的角平分线上?请说明理由.
(3)证明:AB=PC.
23.数学学习不仅要理解概念的本质,而且还要记忆相关的结论,这样我们才能明白数学问题的意义,才能有数学的意识解决数学实际问题.
(1)叙述角平分线性质定理: ;
(2)叙述并证明角平分线性质定理的逆定理.
24.我们已经学习过角平分线性质定理,即:角平分线上的点到角两边的距离相等.
如图,已知△ABC的角平分线BD交边AC于点D.
(1)求证:=;
(2)求证:=;
(3)如果BC=4,AB=6,AC=5,那么CD= .
答案
一.选择题
A.C.C.D.B.B.B.C.D.C.
二.填空题
11.3.
12.1.
13.10:11:12.
14.3.
15.6.
16.4.
17.28.
18.6.
三.解答题
19.证明:如图,在△ABC中,角平分线BM与角平分线CN相交于点P,过点P分别作AB,BC,AC的垂线,垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,且PD⊥AB,PE⊥BC,垂足分别为D,E,
∴PD=PE(角平分线上的点到这个角的两边的距离相等).
同理,PE=PF.
∴PD=PE=PF.
∴点P在∠A的平分线上(在一个角的内部,到角的两边距离相等的点在这个角的平分线上),
即∠A的平分线经过点P.
故三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
20.证明:∵AE平分∠BAD,DE平分∠ADC,
∴∠1=∠3,∠2=∠4,
∵AB⊥BC,∠1+∠2=90°,
∴∠ABE=90°,∠AED=90°,∠4+∠1=90°,
∴∠3+∠6=90°,∠6+∠5=90°,
∴∠3=∠5,
∴∠4+∠5=90°,
∴∠DCE=180°﹣∠4﹣∠5=90°,
∴DC⊥BC.
21.(1)∠ABC的平分线如图所示.
(2)作DH⊥AB于H.
∵BD平分∠ABC,DC⊥BC,DH⊥AB,
∴CD=DH=3,
∴△ABC的面积=S△BCD+S△ABD=BC CD+AB DH=×3BC+3AB=(BC+AB)=3×16=24.
22.(1)∵P点是∠ABC和∠ACB角平分线的交点,
∴∠CBP=∠ABP=∠ABC,∠BCP=∠ACP=∠ACB,
∵∠ABC=60°,∠ACB=40°,
∴∠PBC+∠PCB=∠ABC+∠ACB=30°+20°=50°,
∴∠BPC=180°﹣50°=130°,
故答案为:130°;
(2)答:点P在∠BAC的角平分线上,理由如下:
过点p分别作三角形三边的垂线,垂足分别为D、E、F,
∵PB、PC分别是∠ABC、∠ACB 的角平分线,
∴PD=PE PE=PF,
∴PD=PF,
∴点P在∠BAC的角平分线上;
(3)证明:延长AP,在AP延长线上取PG=PC,连接GC,
∵AP、CP分别为∠BAC、∠ACB的平分线,
∴∠PAC=40°,∠ACP=20°,
∴∠GPC=∠PAC+∠ACP=60°,
∴△PGC为等边三角形,
∴∠G=60°=∠ABC,PC=CG,
在△ABC和△CGA中,
,
∴△ABC≌△CGA(AAS),
∴AB=CG,
又∵PC=CG,
故AB=PC.
23.(1)角平分线性质定理:角平分线上的任意一点,到角两边的距离相等.
故答案为:角平分线上的任意一点,到角两边的距离相等;
(2)角平分线性质定理的逆定理:到角的两边的距离相等的点在这个角的平分线上;
已知:如图,点P在∠AOB的内部,PC⊥OA,PD⊥OB,垂足分别为C、D,且PC=PD.
求证:点P在∠AOB的平分线上,
证明:如图,
∵PC⊥OA,PD⊥OB,
∴∠PCO=∠PDO=90°,
在Rt△PCO和Rt△PDO中,
,
∴Rt△PCO≌Rt△PDO(HL),
∴∠POC=∠POD,
∴OP是∠AOB的平分线,
即点P在∠AOB的平分线上.
24.(1)证明:作DF⊥BC于F点,作DH⊥AB于H点,如图,
∵BD是△ABC的角平分线,
∴DF=DH,
∴==;
(2)证明:作BE⊥CA于E点,如图,
∵==,
∵=;
∴=;
(3)解:∵=,
∴==,
∴=,即=,
∴CD=AC=×5=2.
故答案为:2.
