人教版八年级数学上册试题 13.2画轴对称图形(含答案)
文档属性
| 名称 | 人教版八年级数学上册试题 13.2画轴对称图形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-20 10:18:11 | ||
图片预览



文档简介
13.2画轴对称图形
一、单选题
1.在平面直角坐标系中,点和点关于轴对称,的值是( )
A. B. C. D.
2.2022年2月4日至2月20日,第24届冬奥会在中国北京市和张家口市联合举办.下列冬奥元素中是轴对称图形的是( )
A. B.C.D.
3.已知点和点关于轴对称,则的值为( )
A.7 B.1 C.-1 D.-7
4.在平面直角坐标系xOy中,点关于x轴的对称点的坐标为( )
A. B. C. D.
5.如图,将一个长方形纸条折成如图的形状,若已知,则的度数为( )
A.63° B.54° C.72° D.45°
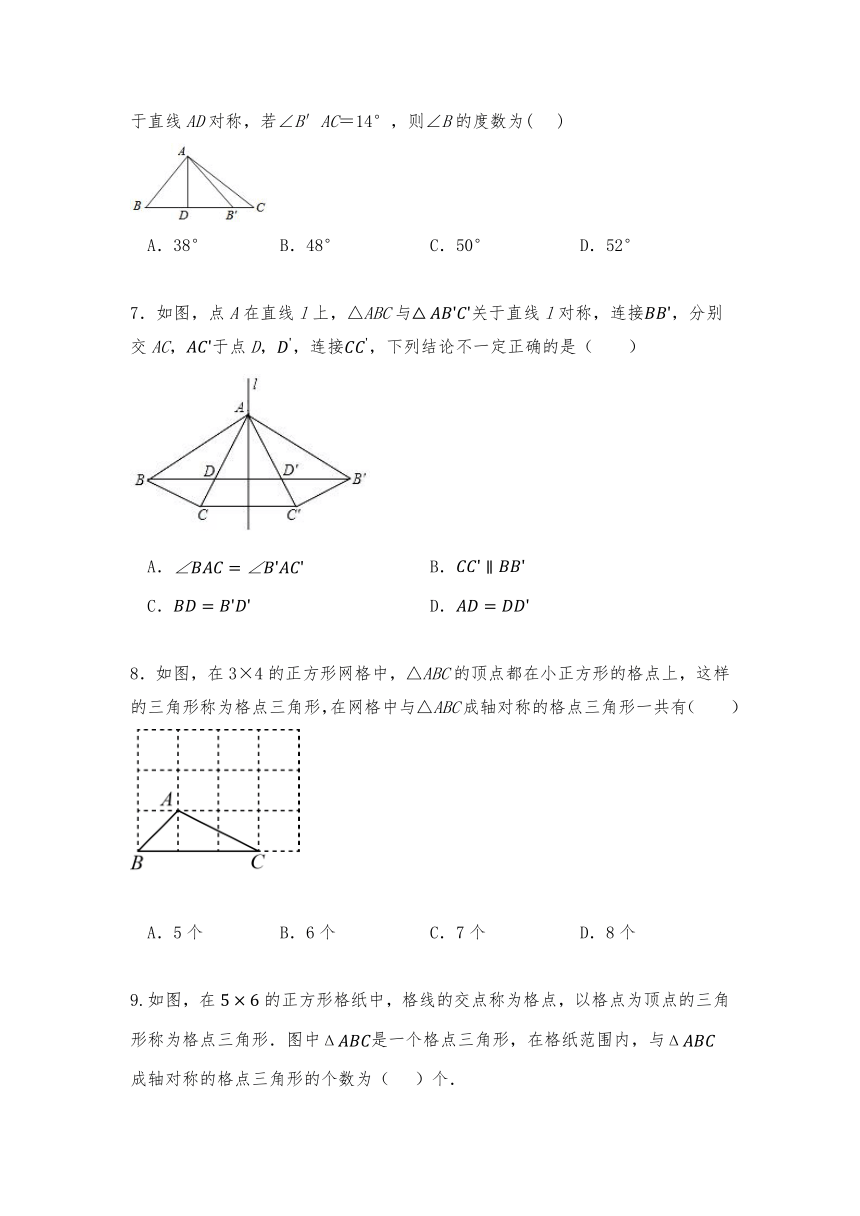
6.如图,在Rt△ACB中,∠BAC=90°,AD⊥BC,垂足为D,△ABD与△ADB′关于直线AD对称,若∠B′AC=14°,则∠B的度数为( )
A.38° B.48° C.50° D.52°
7.如图,点A在直线l上,△ABC与关于直线l对称,连接,分别交AC,于点D,,连接,下列结论不一定正确的是( )
A. B.
C. D.
8.如图,在3×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有( )
A.5个 B.6个 C.7个 D.8个
9.如图,在的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中是一个格点三角形,在格纸范围内,与成轴对称的格点三角形的个数为( )个.
A.8 B.9 C.10 D.11
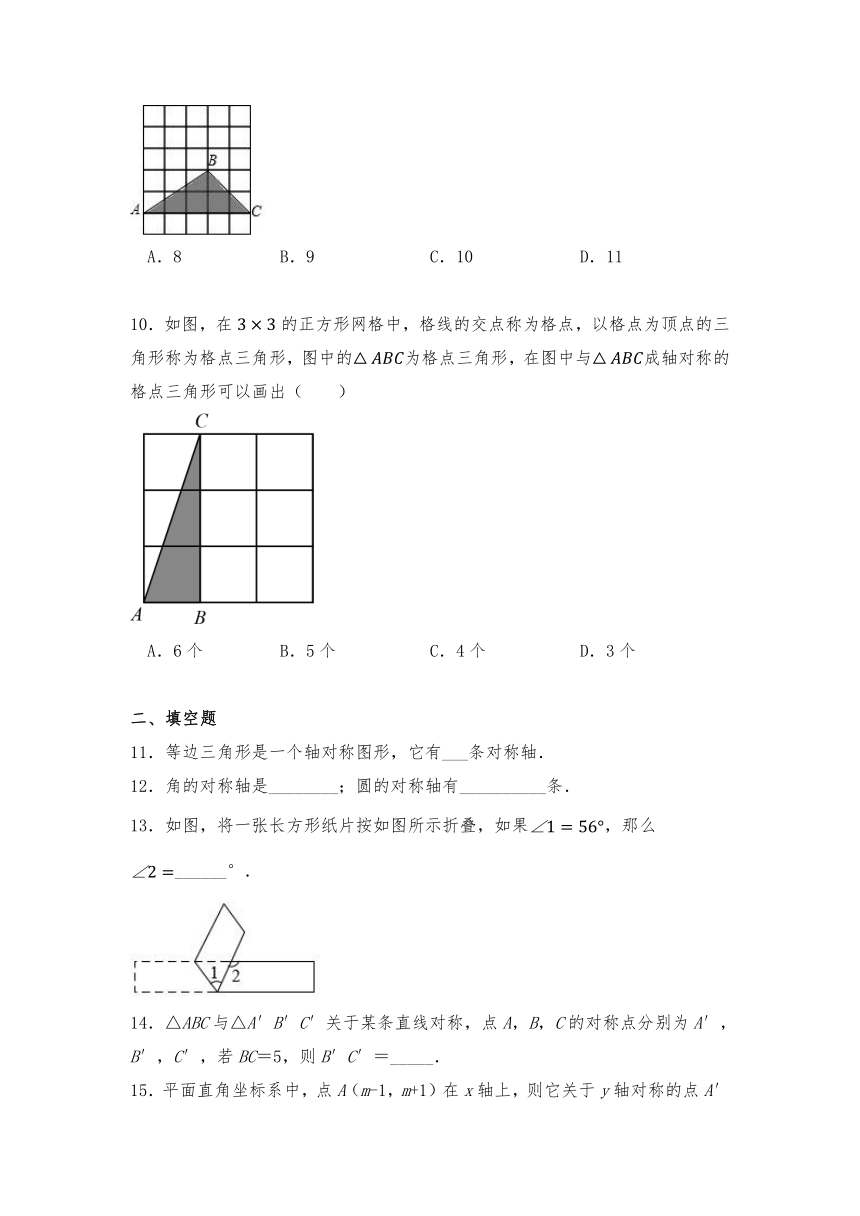
10.如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的为格点三角形,在图中与成轴对称的格点三角形可以画出( )
A.6个 B.5个 C.4个 D.3个
二、填空题
11.等边三角形是一个轴对称图形,它有___条对称轴.
12.角的对称轴是________;圆的对称轴有__________条.
13.如图,将一张长方形纸片按如图所示折叠,如果,那么______°.
14.△ABC与△A′B′C′关于某条直线对称,点A,B,C的对称点分别为A′,B′,C′,若BC=5,则B′C′=_____.
15.平面直角坐标系中,点A(m-1,m+1)在x轴上,则它关于y轴对称的点A′的坐标为______.
16.若点与点关于轴对称,则______.
17.如图,从标有数字1,2,3,4的四个小正方形中拿走一个,成为一个轴对称图形,则应该拿走的小正方形的标号是______.
18.如图是4×4的正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格选出一个也涂成黑色,与原来3个黑色方格组成的图形成为轴对称图形,则符合要求的白色小正方形有___.
三、解答题
19.已知点,若点关于y轴对称,求的值.
20.如图,利用关于坐标轴对称的点的坐标的特点,画出与关于x轴对称的图形.
21.如图,三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)画出关于y轴对称的,
(2)写出三个顶点坐标分别为:______,________,________;
(3)求的面积?
22.如图所示,在正方形网格中,每个小正方形的边长为1个单位.
(1)过直线m作四边形ABCD的对称图形;
(2)直接写出四边形ABCD的面积为 .
23.图1,图2分别是10×6的网格,网格中每个小正方形的边长均为1,每个网格中画有一个平行四边形,且平行四边形的顶点均在格点上(每个小正方形的顶点称为格点),请分别在图1,图2中各画一条线段,使得所画线段均满足以下要求(图1,图2的画法不相同):
(1)线段的一个端点为平行四边形的顶点,另一个端点在这个平行四边形一边的格点上;
(2)线段将平行四边形分割成两个图形,其中一个图形是轴对称图形.
24.如图①、图②、图③都是3×3的正方形网格,每个小正方形的顶点称为格点.A,B两点均为格点,按下列要求画图:
(1)在图①中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,N均为格点;
(2)在图②中,画以AB为底边的等腰,且C为格点;
(3)在图③中,画一个四边形ABDE,使其为轴对称图形,且D,E均为格点.
答案
一、单选题
B.D.C.C.A.D.D.B.CA.
二、填空题
11.3.
12.这个角平分线所在的直线,无数条.
13.112.
14.5
15.(2,0).
16.2.
17.2.
18.3
三、解答题
19.
解:点关于y轴对称,
,
解得.
.
20.
解:A(-4,1)关于x轴对称点D(-4,-1),B(-1,-1)关于x轴对称点E(-1,1),C(-3,2)关于x轴对称点F(-3,-2),
在坐标系中描出点D(-4,-1),E(-1,1),F(-3,-2),
连接DE、EF、FD,
如图所示,△DEF就是△ABC关于x轴对称的图形.
21.
(1)
解:先作出点A、B、C关于y轴的对称点A1、B1、C1,然后顺次连线,则即为所求作的三角形,如图所示:
(2)
解:根据解析(1)可知,点 的坐标为(-1,1),的坐标为(-4,2),的坐标为(-3,4).
故答案为:(-1,1);(-4,2);(-3,4).
(3)
解:由题意得:
22.解:如图:
(2)解:.
23.
解:(1)如图所示(答案不唯一);
(2)如图所示(答案不唯一).
24.
解:(1)如图①,MN即为所求作;
(2)如图②,△ABC即为所求作;
(3)如图③,四边形ABDE即为所求作.
一、单选题
1.在平面直角坐标系中,点和点关于轴对称,的值是( )
A. B. C. D.
2.2022年2月4日至2月20日,第24届冬奥会在中国北京市和张家口市联合举办.下列冬奥元素中是轴对称图形的是( )
A. B.C.D.
3.已知点和点关于轴对称,则的值为( )
A.7 B.1 C.-1 D.-7
4.在平面直角坐标系xOy中,点关于x轴的对称点的坐标为( )
A. B. C. D.
5.如图,将一个长方形纸条折成如图的形状,若已知,则的度数为( )
A.63° B.54° C.72° D.45°
6.如图,在Rt△ACB中,∠BAC=90°,AD⊥BC,垂足为D,△ABD与△ADB′关于直线AD对称,若∠B′AC=14°,则∠B的度数为( )
A.38° B.48° C.50° D.52°
7.如图,点A在直线l上,△ABC与关于直线l对称,连接,分别交AC,于点D,,连接,下列结论不一定正确的是( )
A. B.
C. D.
8.如图,在3×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有( )
A.5个 B.6个 C.7个 D.8个
9.如图,在的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中是一个格点三角形,在格纸范围内,与成轴对称的格点三角形的个数为( )个.
A.8 B.9 C.10 D.11
10.如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的为格点三角形,在图中与成轴对称的格点三角形可以画出( )
A.6个 B.5个 C.4个 D.3个
二、填空题
11.等边三角形是一个轴对称图形,它有___条对称轴.
12.角的对称轴是________;圆的对称轴有__________条.
13.如图,将一张长方形纸片按如图所示折叠,如果,那么______°.
14.△ABC与△A′B′C′关于某条直线对称,点A,B,C的对称点分别为A′,B′,C′,若BC=5,则B′C′=_____.
15.平面直角坐标系中,点A(m-1,m+1)在x轴上,则它关于y轴对称的点A′的坐标为______.
16.若点与点关于轴对称,则______.
17.如图,从标有数字1,2,3,4的四个小正方形中拿走一个,成为一个轴对称图形,则应该拿走的小正方形的标号是______.
18.如图是4×4的正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格选出一个也涂成黑色,与原来3个黑色方格组成的图形成为轴对称图形,则符合要求的白色小正方形有___.
三、解答题
19.已知点,若点关于y轴对称,求的值.
20.如图,利用关于坐标轴对称的点的坐标的特点,画出与关于x轴对称的图形.
21.如图,三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)画出关于y轴对称的,
(2)写出三个顶点坐标分别为:______,________,________;
(3)求的面积?
22.如图所示,在正方形网格中,每个小正方形的边长为1个单位.
(1)过直线m作四边形ABCD的对称图形;
(2)直接写出四边形ABCD的面积为 .
23.图1,图2分别是10×6的网格,网格中每个小正方形的边长均为1,每个网格中画有一个平行四边形,且平行四边形的顶点均在格点上(每个小正方形的顶点称为格点),请分别在图1,图2中各画一条线段,使得所画线段均满足以下要求(图1,图2的画法不相同):
(1)线段的一个端点为平行四边形的顶点,另一个端点在这个平行四边形一边的格点上;
(2)线段将平行四边形分割成两个图形,其中一个图形是轴对称图形.
24.如图①、图②、图③都是3×3的正方形网格,每个小正方形的顶点称为格点.A,B两点均为格点,按下列要求画图:
(1)在图①中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,N均为格点;
(2)在图②中,画以AB为底边的等腰,且C为格点;
(3)在图③中,画一个四边形ABDE,使其为轴对称图形,且D,E均为格点.
答案
一、单选题
B.D.C.C.A.D.D.B.CA.
二、填空题
11.3.
12.这个角平分线所在的直线,无数条.
13.112.
14.5
15.(2,0).
16.2.
17.2.
18.3
三、解答题
19.
解:点关于y轴对称,
,
解得.
.
20.
解:A(-4,1)关于x轴对称点D(-4,-1),B(-1,-1)关于x轴对称点E(-1,1),C(-3,2)关于x轴对称点F(-3,-2),
在坐标系中描出点D(-4,-1),E(-1,1),F(-3,-2),
连接DE、EF、FD,
如图所示,△DEF就是△ABC关于x轴对称的图形.
21.
(1)
解:先作出点A、B、C关于y轴的对称点A1、B1、C1,然后顺次连线,则即为所求作的三角形,如图所示:
(2)
解:根据解析(1)可知,点 的坐标为(-1,1),的坐标为(-4,2),的坐标为(-3,4).
故答案为:(-1,1);(-4,2);(-3,4).
(3)
解:由题意得:
22.解:如图:
(2)解:.
23.
解:(1)如图所示(答案不唯一);
(2)如图所示(答案不唯一).
24.
解:(1)如图①,MN即为所求作;
(2)如图②,△ABC即为所求作;
(3)如图③,四边形ABDE即为所求作.
