八年级数学上册人教版 13.3.1等腰三角形的判定 试题(含答案)
文档属性
| 名称 | 八年级数学上册人教版 13.3.1等腰三角形的判定 试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 189.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 20:25:25 | ||
图片预览

文档简介
13.3.1等腰三角形的判定
一.选择题
1.在△ABC中,与∠A相邻的外角是130°,要使△ABC为等腰三角形,则∠B的度数是( )
A.50° B.65°
C.50°或65° D.50°或65°或80°
2.如图,正方形的网格中,点A,B是小正方形的顶点,如果C点是小正方形的顶点,且使△ABC是等腰三角形,则点C的个数为( )
A.6 B.7 C.8 D.9
3.如图,网格中的每个小正方形的顶点称作格点,图中A、B在格点上,则图中满足△ABC为等腰三角形的格点C的个数为( )
A.7 B.8 C.9 D.10
4.下列给出的5个图中,能判定△ABC是等腰三角形的有( )
A.2个 B.3个 C.4个 D.5个
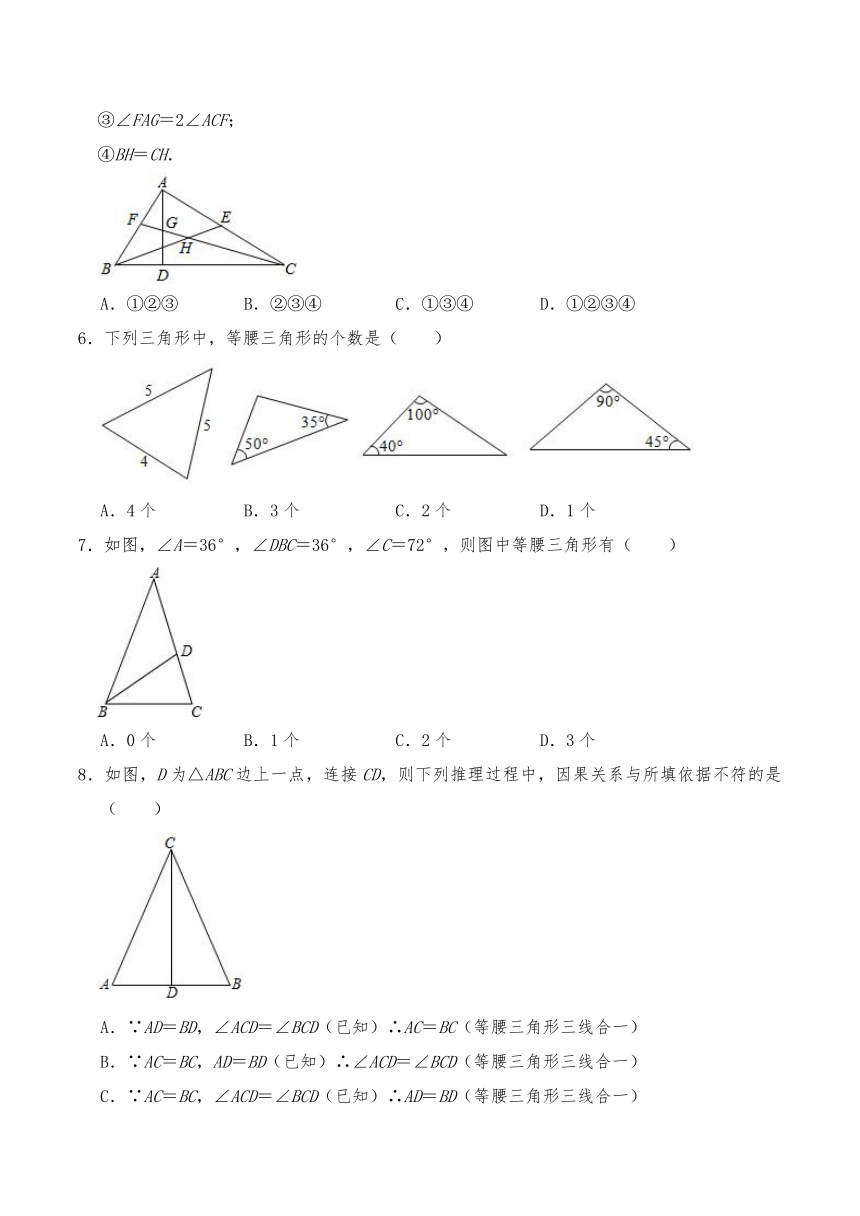
5.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积等于△BCE的面积;
②∠AFG=∠AGF;
③∠FAG=2∠ACF;
④BH=CH.
A.①②③ B.②③④ C.①③④ D.①②③④
6.下列三角形中,等腰三角形的个数是( )
A.4个 B.3个 C.2个 D.1个
7.如图,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有( )
A.0个 B.1个 C.2个 D.3个
8.如图,D为△ABC边上一点,连接CD,则下列推理过程中,因果关系与所填依据不符的是( )
A.∵AD=BD,∠ACD=∠BCD(已知)∴AC=BC(等腰三角形三线合一)
B.∵AC=BC,AD=BD(已知)∴∠ACD=∠BCD(等腰三角形三线合一)
C.∵AC=BC,∠ACD=∠BCD(已知)∴AD=BD(等腰三角形三线合一)
D.∵AC=BC,AD=BD(已知)∴CD⊥AB(等腰三角形三线合一)
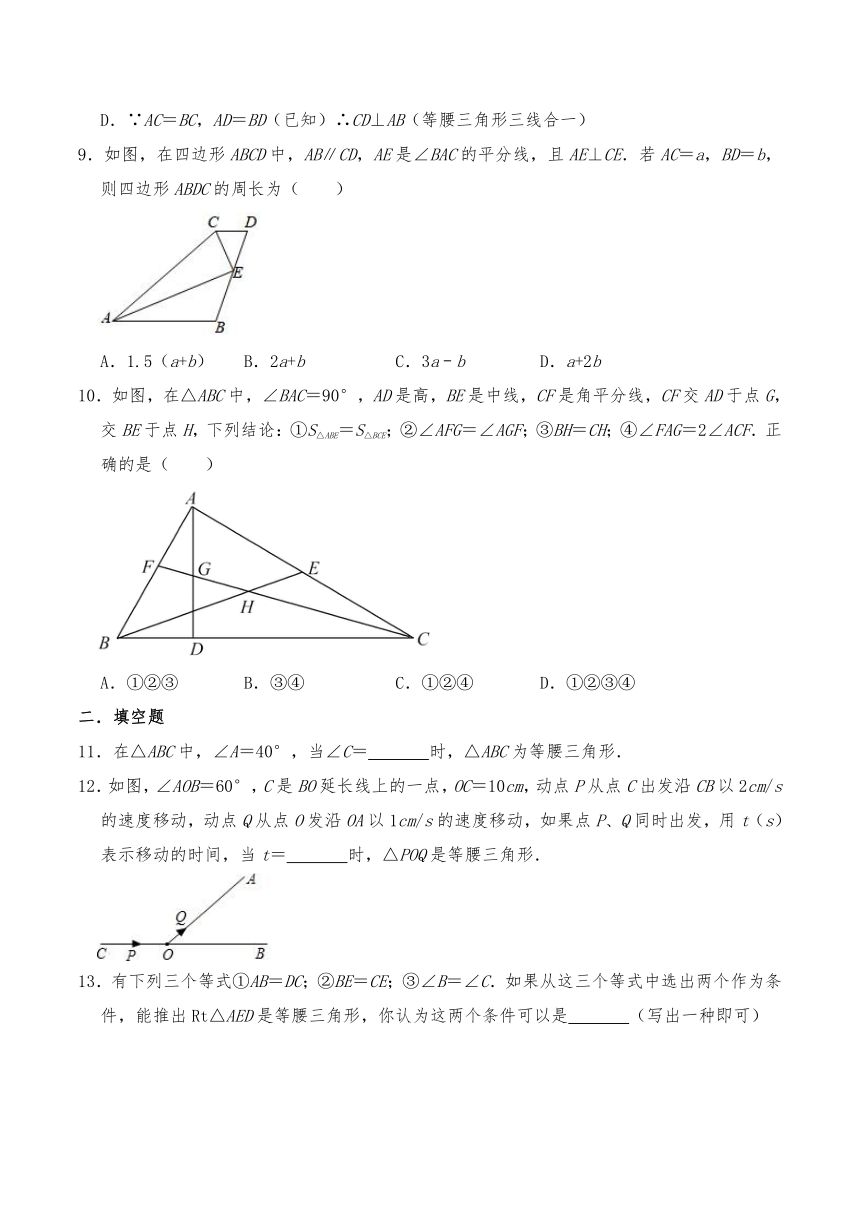
9.如图,在四边形ABCD中,AB∥CD,AE是∠BAC的平分线,且AE⊥CE.若AC=a,BD=b,则四边形ABDC的周长为( )
A.1.5(a+b) B.2a+b C.3a﹣b D.a+2b
10.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③BH=CH;④∠FAG=2∠ACF.正确的是( )
A.①②③ B.③④ C.①②④ D.①②③④
二.填空题
11.在△ABC中,∠A=40°,当∠C= 时,△ABC为等腰三角形.
12.如图,∠AOB=60°,C是BO延长线上的一点,OC=10cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O发沿OA以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t= 时,△POQ是等腰三角形.
13.有下列三个等式①AB=DC;②BE=CE;③∠B=∠C.如果从这三个等式中选出两个作为条件,能推出Rt△AED是等腰三角形,你认为这两个条件可以是 (写出一种即可)
14.已知BD是△ABC的角平分线,E是边AB上一点,DE∥BC,如果DE=6,那么BE= .
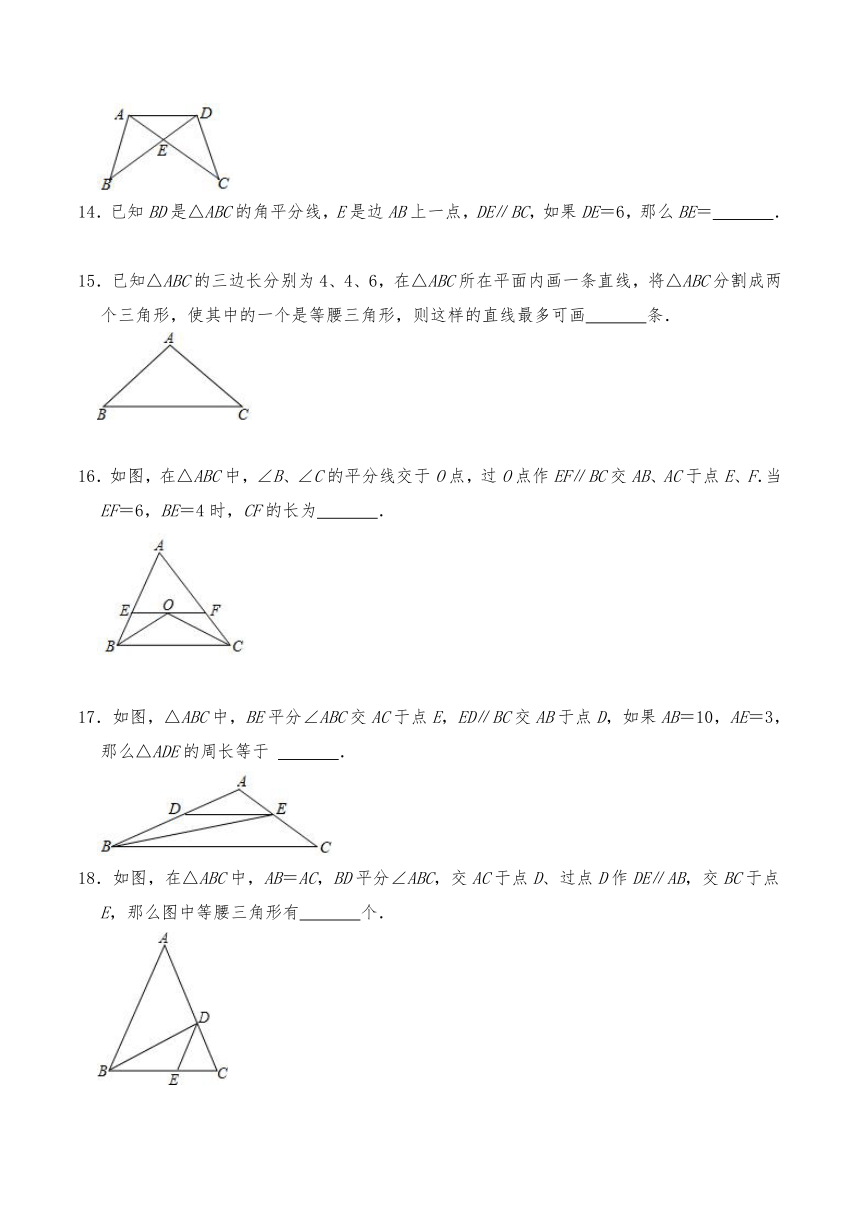
15.已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画 条.
16.如图,在△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于点E、F.当EF=6,BE=4时,CF的长为 .
17.如图,△ABC中,BE平分∠ABC交AC于点E,ED∥BC交AB于点D,如果AB=10,AE=3,那么△ADE的周长等于 .
18.如图,在△ABC中,AB=AC,BD平分∠ABC,交AC于点D、过点D作DE∥AB,交BC于点E,那么图中等腰三角形有 个.
三.解答题
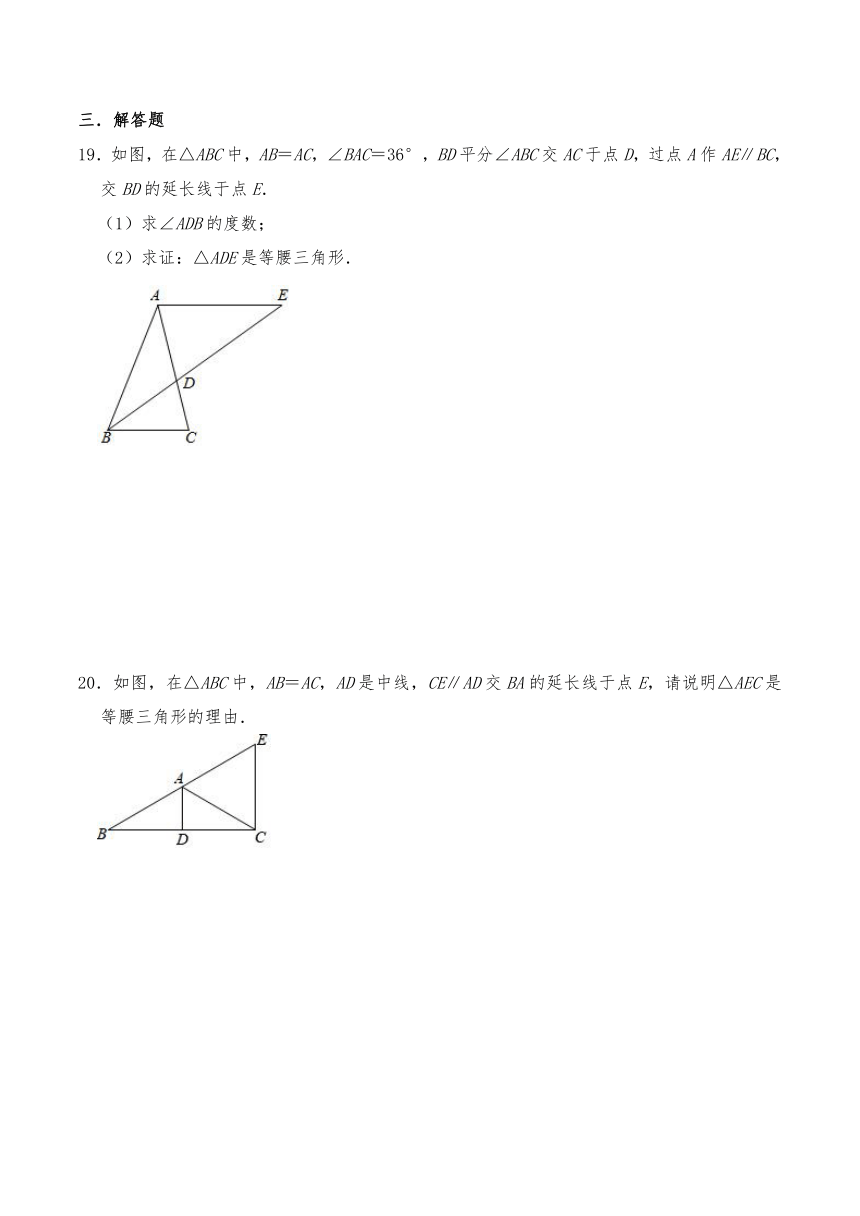
19.如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于点D,过点A作AE∥BC,交BD的延长线于点E.
(1)求∠ADB的度数;
(2)求证:△ADE是等腰三角形.
20.如图,在△ABC中,AB=AC,AD是中线,CE∥AD交BA的延长线于点E,请说明△AEC是等腰三角形的理由.
21.如图,已知在△ABC中,AB=AC=BD,∠ADE=∠B,请说明△ADE是等腰三角形的理由.
22.已知,如图,在△ABC中,AB=AC,D,E分别在CA,BA的延长线上,且BE=CD,连BD,CE.
(1)求证:∠D=∠E;
(2)若∠BAC=108°,∠D=36o,则图中共有 个等腰三角形.
23.已知△ABC中,∠A=70°,BP是∠ABC的平分线,CP是∠ACD的平分线.
(1)如图1,求∠P的度数;
(2)过点P作EF∥BC与边AB、AC分别交于点E、点F(如图2),判断线段BE、EF、CF之间的数量关系,并说明理由.
24.综合与实践:
问题情境:
已知在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D为直线BC上的动点(不与点B,C重合),点E在直线AC上,且AE=AD,设∠DAC=n.
(1)如图1,若点D在BC边上,当n=36°时,求∠BAD和∠CDE的度数;
拓广探索:
(2)如图2,当点D运动到点B的左侧时,其他条件不变,试猜想∠BAD和∠CDE的数量关系,并说明理由;
(3)当点D运动点C的右侧时,其他条件不变,请直接写出∠BAD和∠CDE的数量关系.
答案
一.选择题
D.C.B.C.A.B.D.A.B.C.
二.填空题
11.40°或70°或100°.
12.或10.
13.①②或①③或②③.(答案不唯一)
14.6.
15.4.
16.2.
17.13.
18.3.
三.解答题
19.(1)解:∵AB=AC,∠BAC=36°,
∴∠ABC=∠C=(180°﹣∠BAC)=72°,
∵BD平分∠ABC,
∴∠DBC=∠ABC=36°,
∴∠ADB=∠C+∠DBC=72°+36°=108°;
(2)证明:∵AE∥BC,
∴∠EAC=∠C=72°,
∵∠C=72°,∠DBC=36°,
∴∠ADE=∠CDB=180°﹣72°﹣36°=72°,
∴∠EAD=∠ADE,
∴AE=DE,
∴△ADE是等腰三角形.
20.证明:∵AB=AC,AD是中线,
∴∠BAD=∠CAD,
∵CE∥AD,
∴∠BAD=∠E,
∠DAC=∠ACE,
∴∠E=∠ACE,
∴AC=AE,
∴△AEC是等腰三角形.
21.∵AB=BD,
∴∠BAD=∠BDA,
∵∠ADE=∠B,∠ADE+∠BAD+∠AED=180°,∠B+∠BDA+∠BAD=180°,
∴∠AED=∠BAD,
∴ED=AD,
∴△ADE为等腰三角形.
22.(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
在△EBC和△DCB中,
,
∴△EBC≌△DCB(SAS),
∴∠E=∠D.
(2)图中共有5个等腰三角形.
∵∠BAC=108°,AB=AC,
∴∠ABC=∠ACB=36°,
∵∠D=∠E=36°,
∴∠D=∠BCD,∠E=∠CBE,
∴∠DAB=∠EAC=72°,
∴∠DBA=∠DAB=72°,∠EAC=∠ECA=72°,
∴DB=DA,EA=EC,
∴△ABD,△AEC,△BCD,△BCE,△ABC是等腰三角形.
故答案为:5.
23.(1)∵BP是∠ABC的平分线,CP是∠ACD的平分线,
∴∠PBC=∠ABC,∠PCD=∠ACD,
∴∠P=∠PCD﹣∠PBD=∠ACD﹣∠ABC=(∠ACD﹣∠ABC)=∠A=×70°=35°;
(2)BE=EF+CF.
理由:∵BP是∠ABC的平分线,CP是∠ACD的平分线,
∴∠ABP=∠PBD,∠ACP=∠PCD,
∵EF∥BC,
∴∠EPB=∠PBD,∠EPC=∠PCD,
∴∠ABP=∠EPB,∠ACP=∠EPC,
∴BE=PE,CF=PF,
∵PE=EF+PF,
∴BE=EF+CF.
24.(1)∠BAD=∠BAC﹣∠DAC=100°﹣36°=64°.
∵在△ABC中,∠BAC=100°,∠ABC=∠ACB,
∴∠ABC=∠ACB=40°,
∴∠ADC=∠ABC+∠BAD=40°+64°=104°.
∵AE=AD,
∴∠ADE=∠AED.
∵∠DAC=36°,
∴∠ADE=∠AED=72°.
∴∠CDE=∠ADC﹣∠ADE=104°﹣72°=32°.
(2)∠BAD=2∠CDE.理由如下:
在△ABC中,∠BAC=100°,
∴∠ABC=∠ACB=40°.
在△ADE中,∠DAC=n,
∴.
∵∠ACB=∠CDE+∠E,
∴=.
∵∠BAC=100°,∠DAC=n,
∴∠BAD=n﹣100°.
∴∠BAD=2∠CDE.
(3)∠BAD=2∠CDE,理由如下:
如图③,在△ABC中,∠BAC=100°,
∴∠ABC=∠ACB=40°,
∴∠ACD=140°.
在△ADE中,∠DAC=n,
∴∠ADE=∠AED=.
∵∠ACD=∠CDE+∠AED,
∴∠CDE=∠ACD﹣∠AED=140°﹣=,
∵∠BAC=100°,∠DAC=n,
∴∠BAD=100°+n,
∴∠BAD=2∠CDE.
一.选择题
1.在△ABC中,与∠A相邻的外角是130°,要使△ABC为等腰三角形,则∠B的度数是( )
A.50° B.65°
C.50°或65° D.50°或65°或80°
2.如图,正方形的网格中,点A,B是小正方形的顶点,如果C点是小正方形的顶点,且使△ABC是等腰三角形,则点C的个数为( )
A.6 B.7 C.8 D.9
3.如图,网格中的每个小正方形的顶点称作格点,图中A、B在格点上,则图中满足△ABC为等腰三角形的格点C的个数为( )
A.7 B.8 C.9 D.10
4.下列给出的5个图中,能判定△ABC是等腰三角形的有( )
A.2个 B.3个 C.4个 D.5个
5.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积等于△BCE的面积;
②∠AFG=∠AGF;
③∠FAG=2∠ACF;
④BH=CH.
A.①②③ B.②③④ C.①③④ D.①②③④
6.下列三角形中,等腰三角形的个数是( )
A.4个 B.3个 C.2个 D.1个
7.如图,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有( )
A.0个 B.1个 C.2个 D.3个
8.如图,D为△ABC边上一点,连接CD,则下列推理过程中,因果关系与所填依据不符的是( )
A.∵AD=BD,∠ACD=∠BCD(已知)∴AC=BC(等腰三角形三线合一)
B.∵AC=BC,AD=BD(已知)∴∠ACD=∠BCD(等腰三角形三线合一)
C.∵AC=BC,∠ACD=∠BCD(已知)∴AD=BD(等腰三角形三线合一)
D.∵AC=BC,AD=BD(已知)∴CD⊥AB(等腰三角形三线合一)
9.如图,在四边形ABCD中,AB∥CD,AE是∠BAC的平分线,且AE⊥CE.若AC=a,BD=b,则四边形ABDC的周长为( )
A.1.5(a+b) B.2a+b C.3a﹣b D.a+2b
10.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③BH=CH;④∠FAG=2∠ACF.正确的是( )
A.①②③ B.③④ C.①②④ D.①②③④
二.填空题
11.在△ABC中,∠A=40°,当∠C= 时,△ABC为等腰三角形.
12.如图,∠AOB=60°,C是BO延长线上的一点,OC=10cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O发沿OA以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t= 时,△POQ是等腰三角形.
13.有下列三个等式①AB=DC;②BE=CE;③∠B=∠C.如果从这三个等式中选出两个作为条件,能推出Rt△AED是等腰三角形,你认为这两个条件可以是 (写出一种即可)
14.已知BD是△ABC的角平分线,E是边AB上一点,DE∥BC,如果DE=6,那么BE= .
15.已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画 条.
16.如图,在△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于点E、F.当EF=6,BE=4时,CF的长为 .
17.如图,△ABC中,BE平分∠ABC交AC于点E,ED∥BC交AB于点D,如果AB=10,AE=3,那么△ADE的周长等于 .
18.如图,在△ABC中,AB=AC,BD平分∠ABC,交AC于点D、过点D作DE∥AB,交BC于点E,那么图中等腰三角形有 个.
三.解答题
19.如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于点D,过点A作AE∥BC,交BD的延长线于点E.
(1)求∠ADB的度数;
(2)求证:△ADE是等腰三角形.
20.如图,在△ABC中,AB=AC,AD是中线,CE∥AD交BA的延长线于点E,请说明△AEC是等腰三角形的理由.
21.如图,已知在△ABC中,AB=AC=BD,∠ADE=∠B,请说明△ADE是等腰三角形的理由.
22.已知,如图,在△ABC中,AB=AC,D,E分别在CA,BA的延长线上,且BE=CD,连BD,CE.
(1)求证:∠D=∠E;
(2)若∠BAC=108°,∠D=36o,则图中共有 个等腰三角形.
23.已知△ABC中,∠A=70°,BP是∠ABC的平分线,CP是∠ACD的平分线.
(1)如图1,求∠P的度数;
(2)过点P作EF∥BC与边AB、AC分别交于点E、点F(如图2),判断线段BE、EF、CF之间的数量关系,并说明理由.
24.综合与实践:
问题情境:
已知在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D为直线BC上的动点(不与点B,C重合),点E在直线AC上,且AE=AD,设∠DAC=n.
(1)如图1,若点D在BC边上,当n=36°时,求∠BAD和∠CDE的度数;
拓广探索:
(2)如图2,当点D运动到点B的左侧时,其他条件不变,试猜想∠BAD和∠CDE的数量关系,并说明理由;
(3)当点D运动点C的右侧时,其他条件不变,请直接写出∠BAD和∠CDE的数量关系.
答案
一.选择题
D.C.B.C.A.B.D.A.B.C.
二.填空题
11.40°或70°或100°.
12.或10.
13.①②或①③或②③.(答案不唯一)
14.6.
15.4.
16.2.
17.13.
18.3.
三.解答题
19.(1)解:∵AB=AC,∠BAC=36°,
∴∠ABC=∠C=(180°﹣∠BAC)=72°,
∵BD平分∠ABC,
∴∠DBC=∠ABC=36°,
∴∠ADB=∠C+∠DBC=72°+36°=108°;
(2)证明:∵AE∥BC,
∴∠EAC=∠C=72°,
∵∠C=72°,∠DBC=36°,
∴∠ADE=∠CDB=180°﹣72°﹣36°=72°,
∴∠EAD=∠ADE,
∴AE=DE,
∴△ADE是等腰三角形.
20.证明:∵AB=AC,AD是中线,
∴∠BAD=∠CAD,
∵CE∥AD,
∴∠BAD=∠E,
∠DAC=∠ACE,
∴∠E=∠ACE,
∴AC=AE,
∴△AEC是等腰三角形.
21.∵AB=BD,
∴∠BAD=∠BDA,
∵∠ADE=∠B,∠ADE+∠BAD+∠AED=180°,∠B+∠BDA+∠BAD=180°,
∴∠AED=∠BAD,
∴ED=AD,
∴△ADE为等腰三角形.
22.(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
在△EBC和△DCB中,
,
∴△EBC≌△DCB(SAS),
∴∠E=∠D.
(2)图中共有5个等腰三角形.
∵∠BAC=108°,AB=AC,
∴∠ABC=∠ACB=36°,
∵∠D=∠E=36°,
∴∠D=∠BCD,∠E=∠CBE,
∴∠DAB=∠EAC=72°,
∴∠DBA=∠DAB=72°,∠EAC=∠ECA=72°,
∴DB=DA,EA=EC,
∴△ABD,△AEC,△BCD,△BCE,△ABC是等腰三角形.
故答案为:5.
23.(1)∵BP是∠ABC的平分线,CP是∠ACD的平分线,
∴∠PBC=∠ABC,∠PCD=∠ACD,
∴∠P=∠PCD﹣∠PBD=∠ACD﹣∠ABC=(∠ACD﹣∠ABC)=∠A=×70°=35°;
(2)BE=EF+CF.
理由:∵BP是∠ABC的平分线,CP是∠ACD的平分线,
∴∠ABP=∠PBD,∠ACP=∠PCD,
∵EF∥BC,
∴∠EPB=∠PBD,∠EPC=∠PCD,
∴∠ABP=∠EPB,∠ACP=∠EPC,
∴BE=PE,CF=PF,
∵PE=EF+PF,
∴BE=EF+CF.
24.(1)∠BAD=∠BAC﹣∠DAC=100°﹣36°=64°.
∵在△ABC中,∠BAC=100°,∠ABC=∠ACB,
∴∠ABC=∠ACB=40°,
∴∠ADC=∠ABC+∠BAD=40°+64°=104°.
∵AE=AD,
∴∠ADE=∠AED.
∵∠DAC=36°,
∴∠ADE=∠AED=72°.
∴∠CDE=∠ADC﹣∠ADE=104°﹣72°=32°.
(2)∠BAD=2∠CDE.理由如下:
在△ABC中,∠BAC=100°,
∴∠ABC=∠ACB=40°.
在△ADE中,∠DAC=n,
∴.
∵∠ACB=∠CDE+∠E,
∴=.
∵∠BAC=100°,∠DAC=n,
∴∠BAD=n﹣100°.
∴∠BAD=2∠CDE.
(3)∠BAD=2∠CDE,理由如下:
如图③,在△ABC中,∠BAC=100°,
∴∠ABC=∠ACB=40°,
∴∠ACD=140°.
在△ADE中,∠DAC=n,
∴∠ADE=∠AED=.
∵∠ACD=∠CDE+∠AED,
∴∠CDE=∠ACD﹣∠AED=140°﹣=,
∵∠BAC=100°,∠DAC=n,
∴∠BAD=100°+n,
∴∠BAD=2∠CDE.
