八年级数学上册人教版 13.3.1等腰三角形的性质 试题(含答案)
文档属性
| 名称 | 八年级数学上册人教版 13.3.1等腰三角形的性质 试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 274.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 00:00:00 | ||
图片预览


文档简介
13.3.1等腰三角形的性质
一.选择题
1.如图,在△ABC中,AB=AC,AD⊥BC,若∠BAC=110°,则∠BAD的度数为( )
A.35° B.55° C.65° D.90°
2.等腰三角形两边长分别为3和6,则该三角形的周长为( )
A.12 B.15
C.12或15 D.条件不够无法计算
3.如图,在△ABC中,AB=AC,∠A=40°,直线DE垂直平分AB垂足为点E,DE交AC于点D,连接BD,则∠DBC的度数为( )
A.30° B.40° C.55° D.75°
4.若一个等腰三角形有一个内角为82°,则它的底角为( )
A.82° B.16° C.82°或49° D.82°或36°
5.等腰三角形的一个外角为102°,则等腰三角形的顶角为( )
A.24° B.78° C.24°或78° D.102°
6.如图,△ABC中,AB=AC,D是BC的中点,∠BAC=50°,则∠BAD的度数为( )
A.25° B.50° C.65° D.100°
7.如图,在△ABC中,AB=AC,AD为BC边上的中线,∠B=25°,则∠CAD的度数为( )
A.55° B.65° C.75° D.85°
8.如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为( )
A.30° B.34° C.36° D.40°
9.如图,在△ABC中,∠BAC=α,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,则∠DAE的大小为( )
A.α B. C. D.α
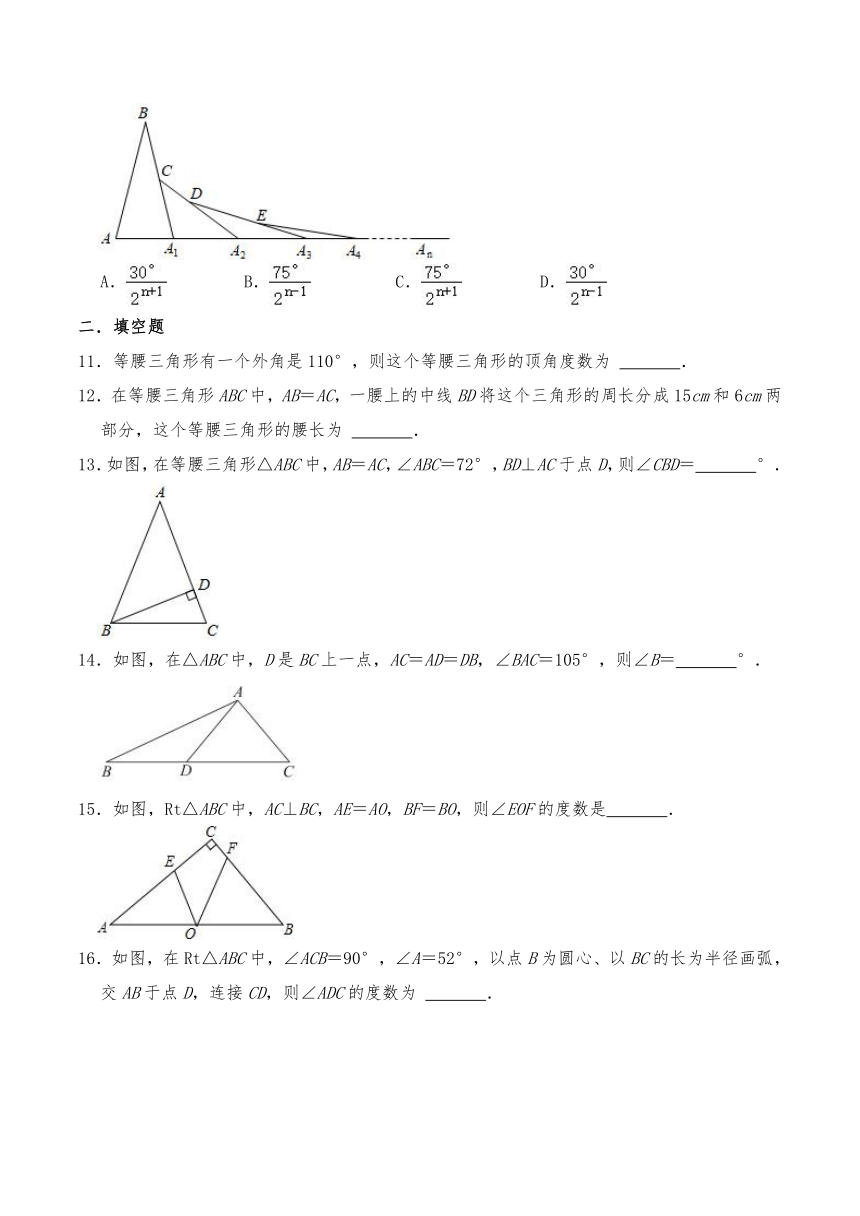
10.如图,在第1个△ABA1中,∠B=30°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…按此作法进行下去,第n个三角形的以An为顶点的内角的度数为( )
A. B. C. D.
二.填空题
11.等腰三角形有一个外角是110°,则这个等腰三角形的顶角度数为 .
12.在等腰三角形ABC中,AB=AC,一腰上的中线BD将这个三角形的周长分成15cm和6cm两部分,这个等腰三角形的腰长为 .
13.如图,在等腰三角形△ABC中,AB=AC,∠ABC=72°,BD⊥AC于点D,则∠CBD= °.
14.如图,在△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,则∠B= °.
15.如图,Rt△ABC中,AC⊥BC,AE=AO,BF=BO,则∠EOF的度数是 .
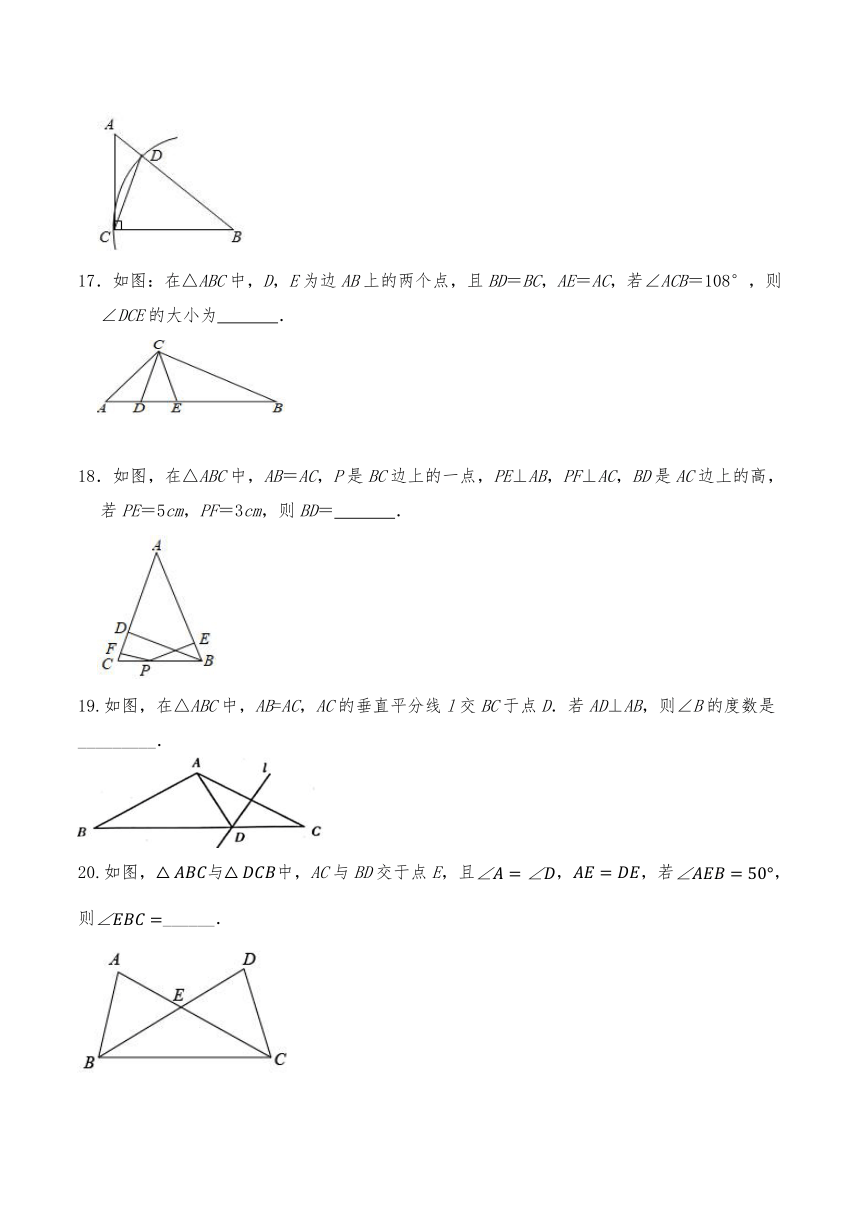
16.如图,在Rt△ABC中,∠ACB=90°,∠A=52°,以点B为圆心、以BC的长为半径画弧,交AB于点D,连接CD,则∠ADC的度数为 .
17.如图:在△ABC中,D,E为边AB上的两个点,且BD=BC,AE=AC,若∠ACB=108°,则∠DCE的大小为 .
18.如图,在△ABC中,AB=AC,P是BC边上的一点,PE⊥AB,PF⊥AC,BD是AC边上的高,若PE=5cm,PF=3cm,则BD= .
19.如图,在△ABC中,AB=AC,AC的垂直平分线l交BC于点D.若AD⊥AB,则∠B的度数是_________.
20.如图,与中,AC与BD交于点E,且,,若,则______.
三.解答题
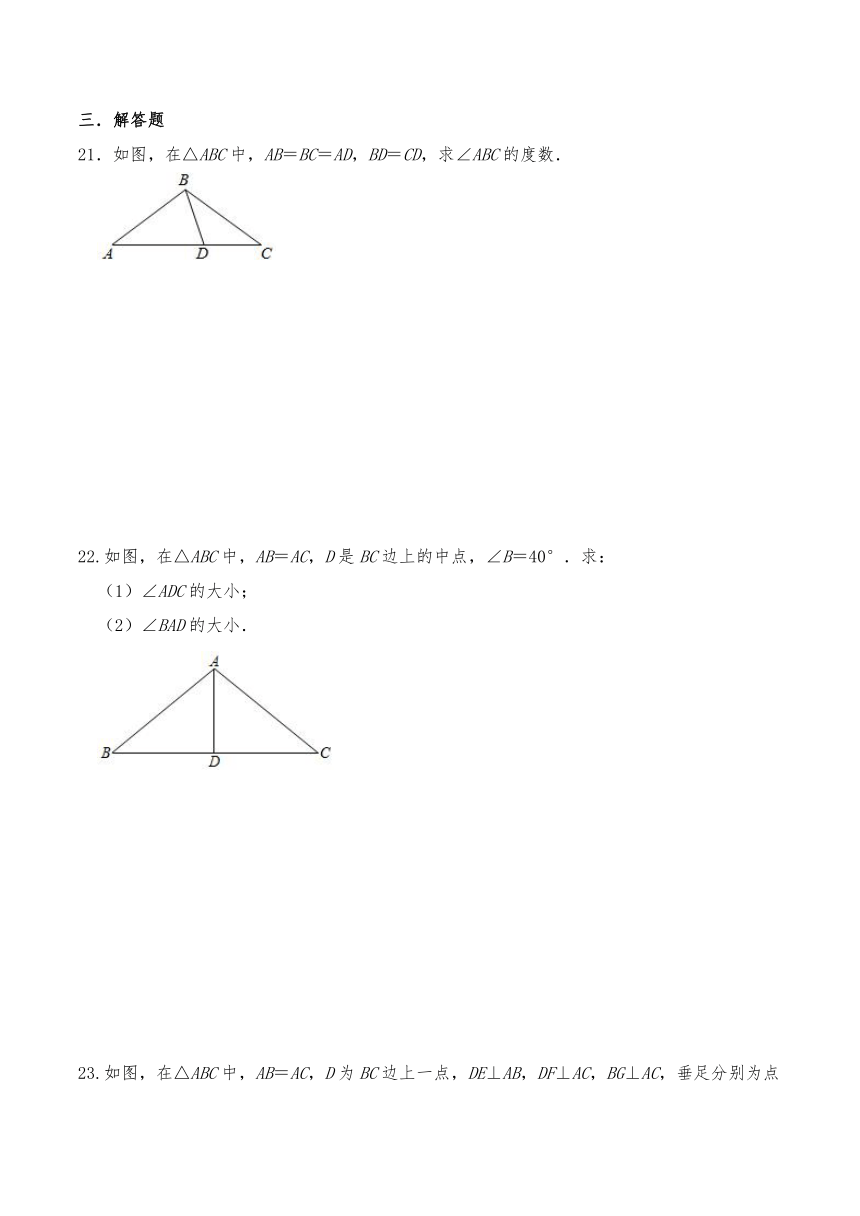
21.如图,在△ABC中,AB=BC=AD,BD=CD,求∠ABC的度数.
22.如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=40°.求:
(1)∠ADC的大小;
(2)∠BAD的大小.
23.如图,在△ABC中,AB=AC,D为BC边上一点,DE⊥AB,DF⊥AC,BG⊥AC,垂足分别为点E,F,G.试说明:DE+DF=BG.
24.如图,△ABC中,AB=AC,∠BAC=100°,AD是BC边上的中线,E是AB上一点且BD=BE,求∠ADE的度数.
25.若a、b是△ABC的两边且|a﹣3|+(b﹣4)2=0
(1)试求a、b的值,并求第三边c的取值范围.
(2)若△ABC是等腰三角形,试求此三角形的周长.
(3)若另一等腰△DEF,其中一内角为x°,另一个内角为(2x﹣20)°试求此三角形各内角度数.
26.如图,等腰△ABC中,AB=AC,∠ACB=72°,
(1)若BD⊥AC于D,求∠ABD的度数;
(2)若CE平分∠ACB,求证:AE=BC.
27.如图,在中,点D,E分别是边BC,AC上的点,,于点F,于点G,且,求证://.
28.如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.
(1)求证:△ABF≌△ACG;
(2)求证:BE=CG+EG.
答案
一.选择题
B.B.A.C.C.A.B.B.D.B.
二.填空题
11.40°或70°.
12.10cm.
13.18.
14.25.
15.45°.
16.109°.
17.36°.
18.8cm.
19.30°.
20..
三.解答题
21.∵BD=CD,
∴∠BCD=∠CBD,
设∠BCD=∠CBD=x°,
∵AB=BC=AD,
∴∠ABD=∠ADB=∠BCD+∠CBD=2x°,∠A=∠C=x°,
∴∠ABC=3∠C=3x°,
∵∠B+∠ABC+∠C=180°,
∴5x=180,
解得x=36,
∴∠C=36°
∴∠ABC=3∠C=108°.
22.(1)∵AB=AC,D是BC边上的中点,
∴AD⊥BC,即∠ADC=90°;
(2)∵∠B=40°,
∴∠BAD=50°.
23.证明:连接AD.
则△ABC的面积=△ABD的面积+△ACD的面积,
AB DE+AC DF=AC BG,
∵AB=AC,
∴DE+DF=BG.
24.∵AB=AC,∠BAC=100°,
∴∠B=∠C=40°,
∵BD=BE,
∴∠BDE=∠BED=70°,
∵AB=AC,AD是BC边上的中线,
∴∠ADB=90°,
∴∠ADE=∠ADB﹣∠BDE=20°.
25.(1)∵|a﹣3|+(b﹣4)2=0,
∴a=3 b=4,
∵b﹣a<c<b+a,
∴1<c<7;
(2)当腰长为3时,此时三角形的三边为3、3、4,满足三角形三边关系,周长为10;
当腰长为4时,此时三角形的三边长为4、4、3,满足三角形三边关系,周长为11;
综上可知等腰三角形的周长为10或11;
(3)当底角为x°、顶角为(2x﹣20)°时,则根据三角形内角和为180°可得
x+x+2x﹣20=180,
解得x=50,
此时三个内角分别为50°、50°、80°;
当顶角为x°、底角为(2x﹣20)°时,则根据三角形内角和为180°可得
x+2x﹣20+2x﹣20=180,
解得x=44,
此时三个内角分别为44°、68°、68°;
当底角为x°、(2x﹣20)°时,则等腰三角形性质可得
x=2x﹣20,
解得x=20,
此时三个内角分别为20°、20°、140°;
综上可知三角形三个内角为50度、50度、80度或44度、68度、68度或20度、20度、140度.
26.(1)∵等腰△ABC中,AB=AC,∠ACB=72°,
∴∠ABC=∠ACB=72°,
∵BD⊥AC于D,
∴∠DBC=90°﹣72°=18°,
∴∠ABD=72°﹣18°=54°;
(2)∵等腰△ABC中,AB=AC,∠ACB=72°,
∴∠ABC=∠ACB=72°,∠A=36°
∵CE平分∠ACB,
∴∠ACE=∠ECB=36°,
∴∠A=∠ACE,
∴AE=EC,
∵∠ABC=72°,
∴∠BEC=72°,
∴BC=CE,
∴AE=BC.
27.解:如图所示,连接AD,
∵DG⊥AC,DF⊥AB,
∴∠DFA=∠DGA=90°,
又∵DF=DG,AD=AD,
∴Rt△ADF≌Rt△ADG(HL)
∴∠DAF=∠DAG,
∵AE=DE,
∴∠EAD=∠EDA,
∴∠DAF=∠EDA,
∴.
28.(1)
∵,
∴,
即 .
在和中,
∵,
∴≌().
(2)
∵≌,
∴,.
∵,于点,
∴.
∵,
∴.
在和中,
∵,
∴≌().
∴.
∴.
一.选择题
1.如图,在△ABC中,AB=AC,AD⊥BC,若∠BAC=110°,则∠BAD的度数为( )
A.35° B.55° C.65° D.90°
2.等腰三角形两边长分别为3和6,则该三角形的周长为( )
A.12 B.15
C.12或15 D.条件不够无法计算
3.如图,在△ABC中,AB=AC,∠A=40°,直线DE垂直平分AB垂足为点E,DE交AC于点D,连接BD,则∠DBC的度数为( )
A.30° B.40° C.55° D.75°
4.若一个等腰三角形有一个内角为82°,则它的底角为( )
A.82° B.16° C.82°或49° D.82°或36°
5.等腰三角形的一个外角为102°,则等腰三角形的顶角为( )
A.24° B.78° C.24°或78° D.102°
6.如图,△ABC中,AB=AC,D是BC的中点,∠BAC=50°,则∠BAD的度数为( )
A.25° B.50° C.65° D.100°
7.如图,在△ABC中,AB=AC,AD为BC边上的中线,∠B=25°,则∠CAD的度数为( )
A.55° B.65° C.75° D.85°
8.如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为( )
A.30° B.34° C.36° D.40°
9.如图,在△ABC中,∠BAC=α,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,则∠DAE的大小为( )
A.α B. C. D.α
10.如图,在第1个△ABA1中,∠B=30°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…按此作法进行下去,第n个三角形的以An为顶点的内角的度数为( )
A. B. C. D.
二.填空题
11.等腰三角形有一个外角是110°,则这个等腰三角形的顶角度数为 .
12.在等腰三角形ABC中,AB=AC,一腰上的中线BD将这个三角形的周长分成15cm和6cm两部分,这个等腰三角形的腰长为 .
13.如图,在等腰三角形△ABC中,AB=AC,∠ABC=72°,BD⊥AC于点D,则∠CBD= °.
14.如图,在△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,则∠B= °.
15.如图,Rt△ABC中,AC⊥BC,AE=AO,BF=BO,则∠EOF的度数是 .
16.如图,在Rt△ABC中,∠ACB=90°,∠A=52°,以点B为圆心、以BC的长为半径画弧,交AB于点D,连接CD,则∠ADC的度数为 .
17.如图:在△ABC中,D,E为边AB上的两个点,且BD=BC,AE=AC,若∠ACB=108°,则∠DCE的大小为 .
18.如图,在△ABC中,AB=AC,P是BC边上的一点,PE⊥AB,PF⊥AC,BD是AC边上的高,若PE=5cm,PF=3cm,则BD= .
19.如图,在△ABC中,AB=AC,AC的垂直平分线l交BC于点D.若AD⊥AB,则∠B的度数是_________.
20.如图,与中,AC与BD交于点E,且,,若,则______.
三.解答题
21.如图,在△ABC中,AB=BC=AD,BD=CD,求∠ABC的度数.
22.如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=40°.求:
(1)∠ADC的大小;
(2)∠BAD的大小.
23.如图,在△ABC中,AB=AC,D为BC边上一点,DE⊥AB,DF⊥AC,BG⊥AC,垂足分别为点E,F,G.试说明:DE+DF=BG.
24.如图,△ABC中,AB=AC,∠BAC=100°,AD是BC边上的中线,E是AB上一点且BD=BE,求∠ADE的度数.
25.若a、b是△ABC的两边且|a﹣3|+(b﹣4)2=0
(1)试求a、b的值,并求第三边c的取值范围.
(2)若△ABC是等腰三角形,试求此三角形的周长.
(3)若另一等腰△DEF,其中一内角为x°,另一个内角为(2x﹣20)°试求此三角形各内角度数.
26.如图,等腰△ABC中,AB=AC,∠ACB=72°,
(1)若BD⊥AC于D,求∠ABD的度数;
(2)若CE平分∠ACB,求证:AE=BC.
27.如图,在中,点D,E分别是边BC,AC上的点,,于点F,于点G,且,求证://.
28.如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.
(1)求证:△ABF≌△ACG;
(2)求证:BE=CG+EG.
答案
一.选择题
B.B.A.C.C.A.B.B.D.B.
二.填空题
11.40°或70°.
12.10cm.
13.18.
14.25.
15.45°.
16.109°.
17.36°.
18.8cm.
19.30°.
20..
三.解答题
21.∵BD=CD,
∴∠BCD=∠CBD,
设∠BCD=∠CBD=x°,
∵AB=BC=AD,
∴∠ABD=∠ADB=∠BCD+∠CBD=2x°,∠A=∠C=x°,
∴∠ABC=3∠C=3x°,
∵∠B+∠ABC+∠C=180°,
∴5x=180,
解得x=36,
∴∠C=36°
∴∠ABC=3∠C=108°.
22.(1)∵AB=AC,D是BC边上的中点,
∴AD⊥BC,即∠ADC=90°;
(2)∵∠B=40°,
∴∠BAD=50°.
23.证明:连接AD.
则△ABC的面积=△ABD的面积+△ACD的面积,
AB DE+AC DF=AC BG,
∵AB=AC,
∴DE+DF=BG.
24.∵AB=AC,∠BAC=100°,
∴∠B=∠C=40°,
∵BD=BE,
∴∠BDE=∠BED=70°,
∵AB=AC,AD是BC边上的中线,
∴∠ADB=90°,
∴∠ADE=∠ADB﹣∠BDE=20°.
25.(1)∵|a﹣3|+(b﹣4)2=0,
∴a=3 b=4,
∵b﹣a<c<b+a,
∴1<c<7;
(2)当腰长为3时,此时三角形的三边为3、3、4,满足三角形三边关系,周长为10;
当腰长为4时,此时三角形的三边长为4、4、3,满足三角形三边关系,周长为11;
综上可知等腰三角形的周长为10或11;
(3)当底角为x°、顶角为(2x﹣20)°时,则根据三角形内角和为180°可得
x+x+2x﹣20=180,
解得x=50,
此时三个内角分别为50°、50°、80°;
当顶角为x°、底角为(2x﹣20)°时,则根据三角形内角和为180°可得
x+2x﹣20+2x﹣20=180,
解得x=44,
此时三个内角分别为44°、68°、68°;
当底角为x°、(2x﹣20)°时,则等腰三角形性质可得
x=2x﹣20,
解得x=20,
此时三个内角分别为20°、20°、140°;
综上可知三角形三个内角为50度、50度、80度或44度、68度、68度或20度、20度、140度.
26.(1)∵等腰△ABC中,AB=AC,∠ACB=72°,
∴∠ABC=∠ACB=72°,
∵BD⊥AC于D,
∴∠DBC=90°﹣72°=18°,
∴∠ABD=72°﹣18°=54°;
(2)∵等腰△ABC中,AB=AC,∠ACB=72°,
∴∠ABC=∠ACB=72°,∠A=36°
∵CE平分∠ACB,
∴∠ACE=∠ECB=36°,
∴∠A=∠ACE,
∴AE=EC,
∵∠ABC=72°,
∴∠BEC=72°,
∴BC=CE,
∴AE=BC.
27.解:如图所示,连接AD,
∵DG⊥AC,DF⊥AB,
∴∠DFA=∠DGA=90°,
又∵DF=DG,AD=AD,
∴Rt△ADF≌Rt△ADG(HL)
∴∠DAF=∠DAG,
∵AE=DE,
∴∠EAD=∠EDA,
∴∠DAF=∠EDA,
∴.
28.(1)
∵,
∴,
即 .
在和中,
∵,
∴≌().
(2)
∵≌,
∴,.
∵,于点,
∴.
∵,
∴.
在和中,
∵,
∴≌().
∴.
∴.
