北师大版数学七年级上册2.4有理数加法第2课时 课件(共14张PPT)
文档属性
| 名称 | 北师大版数学七年级上册2.4有理数加法第2课时 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 444.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-20 13:57:29 | ||
图片预览






文档简介
(共14张PPT)
2.4 有理数的加法(2)
问题2:加法的运算律是不是也可以扩充到
有理数范围?
问题1:在小学中我们学过哪些加法的运算律?
加法交换律:两个数相加,交换加数的位置和不变。
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
忆一忆:
创设情景 明确目标
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c).
(1)(-8)+(-9) (-9)+(-8)
(2) 4+(-7) (-7)+4
(3) [2+(-3)]+(-8) 2+[(-3)+(-8)]
(4) 10+[(-10)+(-5)] [10+(-10)]+(-5)
问题3:说一说,你发现了什么?再试一试
=
=
=
=
算一算:
创设情景 明确目标
通过上面的练习,我们发现在有理数的运算中,加法的_______________依然成立.
加法的运算律
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c).
1.掌握有理数加法的运算律,并能运用加法运
算律简化运算;
2.培养观察、比较、归纳及运算能力,进一步
培养协作学习的能力.
学习目标
计算(1)32+(-27)+(+68)+27
(2)(-1.9)+3.6+(-10.1)+1.4
解:(1)原式=32+___ + (—27) + __
探究点一:有理数加法的运算律
合作探究 达成目标
【反思小结】在使用运算律时,一般先把具有以下特征的数相加:(1)互为相反数的两个数(和为0);(2)相加能得到0的数(凑整);(3)分母相同的数或易通分的数;(4)符号相同的数结合.
68
27
(-10.1)
1.4
解:(2)原式=(-1.9)+ __ + 3.6 + ___
( )
[ ]
( )
[ ]
达标检测 反思目标
例.计算:(+16)+(-25)+(+24)+(-32)
=[______+______]+[______+______]
=( )+( )
=______.
(+16)
(+24)
(-25)
(-32)
-17
40
-57
靶向训练:随堂练习第1、2题。
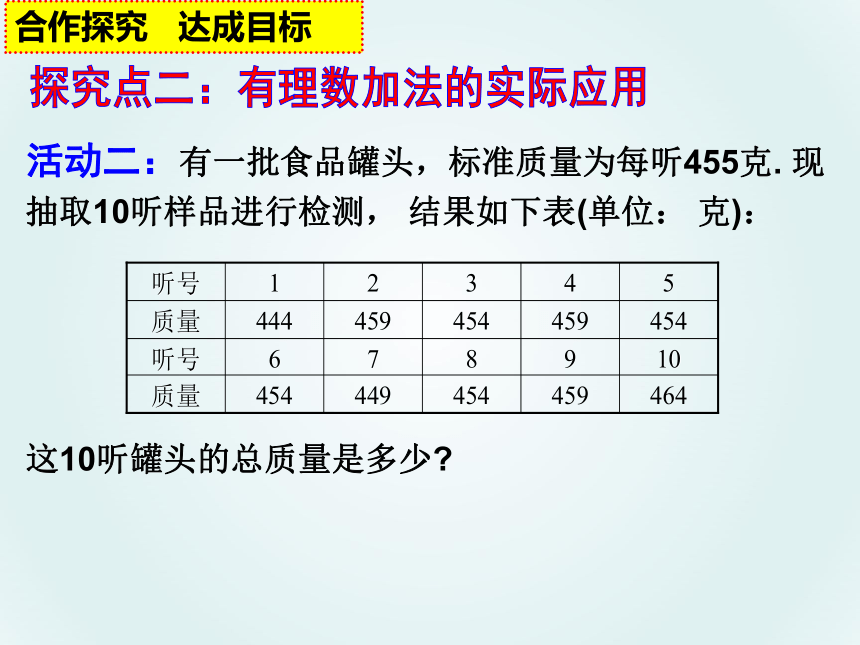
活动二:有一批食品罐头,标准质量为每听455克. 现抽取10听样品进行检测, 结果如下表(单位: 克):
这10听罐头的总质量是多少
探究点二:有理数加法的实际应用
合作探究 达成目标
解法一:这10罐头的总质量为
解法二:把超过标准质量的克数用正数表示,不足 的用负数表示,列出10听关头与标准质量的差值表(单位:克)
444+459+454+459+454+454+449+454+459+464
=4550(克)
这10听罐头的差值和为
(-10)+5+0+5+0+0+(-5)+0+5+10
=[(-10)+10]+[(-5)+5]+5+5
=10(克)
因此,这10听罐头的总质量为
454×10+10
=4540+10
=4550(克)
【展示点评】解法1:直接将10听质量相加获解.解法2:把超过455克的克数记为正数,不足的记为负数,然后把这些数相加.
【小组讨论2】请模仿解决:
8筐白菜,以每筐25千克为准,超过的千克数记作正数,不足的千克数记作负数,称重的记录如下:1.5,-3,2,-0.5,1,-2,-2,-2.5请问8筐白菜的重量是多少?
【靶向训练】39页第2、3题。
探究点二:有理数加法的实际应用
合作探究 达成目标
本课知识:
加法运算律可以使运算简便:①互为相反数的两数可以先相加;②同号的数可以先相加;③分母相同的分数可以先相加;④相加能凑整或凑零的数可以先相加.
总结梳理 内化目标
达标检测 反思目标
1. 下列运算正确的是( )
A. 11+[(-13)+7]=17
B. (-2.5)+[5+(-2.5)]=5
C. [ +( )]+(-2)=-2
D. 3.14+[(-4)+3.14]=-4
2. 一个数是6,另一个数比4的相反数大-2,则
这两个数的和是( )
A.-2 B.-1 C.0 D.1
C
C
达标检测 反思目标
3.在一次区级数学竞赛中,某校8名参赛学生的成
绩与全区参赛学生平均成绩80分的差分别为(单
位:分)5,-2,8,14,7,5,9,-6,则该
校8名参赛学生的平均成绩是______.
85分
达标检测 反思目标
4.计算:(1)(-0.7)+(-0.4)+1+(-0.3)+0.5.
(2)(+15)+(-20)+(+28)+(-10)+(-5)+(-7).
解:(1)原式=[(-0.7)+(-0.3)+1]+[(-0.4)+0.5]
=[(-1)+1]+0.1
=0.1.
(2)原式=[(-10)+(-5)+(+15)]+[(-20)+(-7)]+(
+28)
=[(-15)+(+15)]+[(-27)+(+28)]
=0+1
=1.
2.4 有理数的加法(2)
问题2:加法的运算律是不是也可以扩充到
有理数范围?
问题1:在小学中我们学过哪些加法的运算律?
加法交换律:两个数相加,交换加数的位置和不变。
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
忆一忆:
创设情景 明确目标
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c).
(1)(-8)+(-9) (-9)+(-8)
(2) 4+(-7) (-7)+4
(3) [2+(-3)]+(-8) 2+[(-3)+(-8)]
(4) 10+[(-10)+(-5)] [10+(-10)]+(-5)
问题3:说一说,你发现了什么?再试一试
=
=
=
=
算一算:
创设情景 明确目标
通过上面的练习,我们发现在有理数的运算中,加法的_______________依然成立.
加法的运算律
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c).
1.掌握有理数加法的运算律,并能运用加法运
算律简化运算;
2.培养观察、比较、归纳及运算能力,进一步
培养协作学习的能力.
学习目标
计算(1)32+(-27)+(+68)+27
(2)(-1.9)+3.6+(-10.1)+1.4
解:(1)原式=32+___ + (—27) + __
探究点一:有理数加法的运算律
合作探究 达成目标
【反思小结】在使用运算律时,一般先把具有以下特征的数相加:(1)互为相反数的两个数(和为0);(2)相加能得到0的数(凑整);(3)分母相同的数或易通分的数;(4)符号相同的数结合.
68
27
(-10.1)
1.4
解:(2)原式=(-1.9)+ __ + 3.6 + ___
( )
[ ]
( )
[ ]
达标检测 反思目标
例.计算:(+16)+(-25)+(+24)+(-32)
=[______+______]+[______+______]
=( )+( )
=______.
(+16)
(+24)
(-25)
(-32)
-17
40
-57
靶向训练:随堂练习第1、2题。
活动二:有一批食品罐头,标准质量为每听455克. 现抽取10听样品进行检测, 结果如下表(单位: 克):
这10听罐头的总质量是多少
探究点二:有理数加法的实际应用
合作探究 达成目标
解法一:这10罐头的总质量为
解法二:把超过标准质量的克数用正数表示,不足 的用负数表示,列出10听关头与标准质量的差值表(单位:克)
444+459+454+459+454+454+449+454+459+464
=4550(克)
这10听罐头的差值和为
(-10)+5+0+5+0+0+(-5)+0+5+10
=[(-10)+10]+[(-5)+5]+5+5
=10(克)
因此,这10听罐头的总质量为
454×10+10
=4540+10
=4550(克)
【展示点评】解法1:直接将10听质量相加获解.解法2:把超过455克的克数记为正数,不足的记为负数,然后把这些数相加.
【小组讨论2】请模仿解决:
8筐白菜,以每筐25千克为准,超过的千克数记作正数,不足的千克数记作负数,称重的记录如下:1.5,-3,2,-0.5,1,-2,-2,-2.5请问8筐白菜的重量是多少?
【靶向训练】39页第2、3题。
探究点二:有理数加法的实际应用
合作探究 达成目标
本课知识:
加法运算律可以使运算简便:①互为相反数的两数可以先相加;②同号的数可以先相加;③分母相同的分数可以先相加;④相加能凑整或凑零的数可以先相加.
总结梳理 内化目标
达标检测 反思目标
1. 下列运算正确的是( )
A. 11+[(-13)+7]=17
B. (-2.5)+[5+(-2.5)]=5
C. [ +( )]+(-2)=-2
D. 3.14+[(-4)+3.14]=-4
2. 一个数是6,另一个数比4的相反数大-2,则
这两个数的和是( )
A.-2 B.-1 C.0 D.1
C
C
达标检测 反思目标
3.在一次区级数学竞赛中,某校8名参赛学生的成
绩与全区参赛学生平均成绩80分的差分别为(单
位:分)5,-2,8,14,7,5,9,-6,则该
校8名参赛学生的平均成绩是______.
85分
达标检测 反思目标
4.计算:(1)(-0.7)+(-0.4)+1+(-0.3)+0.5.
(2)(+15)+(-20)+(+28)+(-10)+(-5)+(-7).
解:(1)原式=[(-0.7)+(-0.3)+1]+[(-0.4)+0.5]
=[(-1)+1]+0.1
=0.1.
(2)原式=[(-10)+(-5)+(+15)]+[(-20)+(-7)]+(
+28)
=[(-15)+(+15)]+[(-27)+(+28)]
=0+1
=1.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
