2.4有理数的加法课件
图片预览




文档简介
课件12张PPT。2.4有理数的加法运算
引 言
一、复习提问
1、下列各组数中,哪一个数的绝对值大?
(1)7和4; (2)-7和4; (3)7和-4; (4)-7和-4。
2、说明下列用负数表示的量的实际意义
(1)小兰第一次前进了5米,接着按同一方向又前进了-2米;
(2)北京的气温第一天上升了3℃,第二天又上升了-1℃;
(3)东方汽车向东走了4千米之后,再向东走了-2千米。
3、根据上述问题,回答
(1)小兰两次一共前进了几米?
(2)北京的气温两天一共上升了几度?
(3)东方汽车一共向东走了几千米?
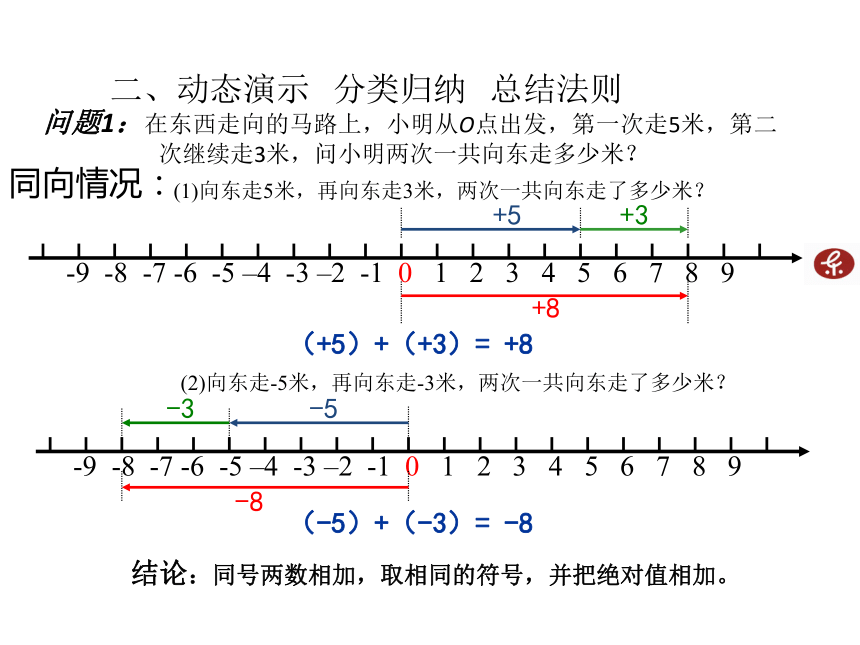
二、动态演示 分类归纳 总结法则问题1:在东西走向的马路上,小明从O点出发,第一次走5米,第二次继续走3米,问小明两次一共向东走多少米?
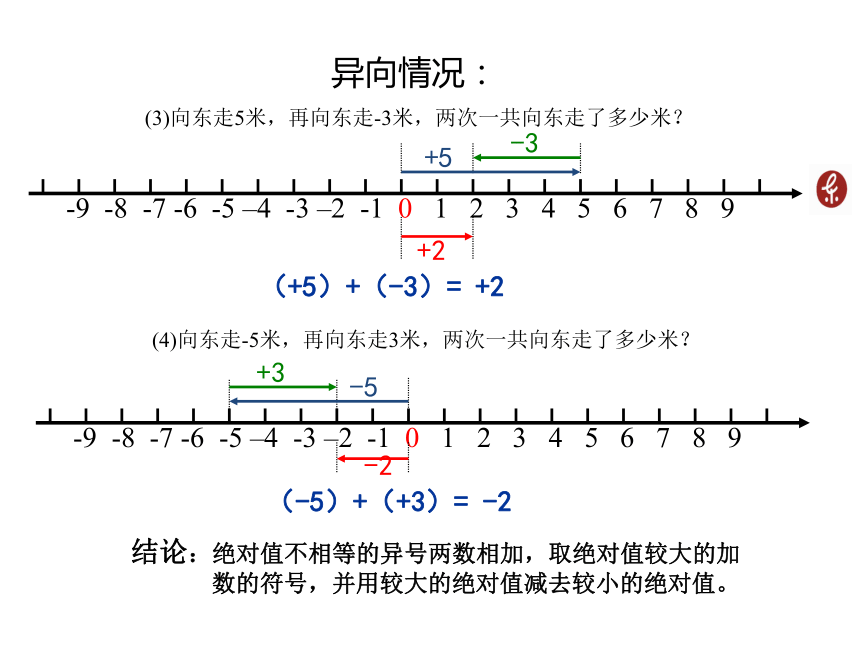
(1)向东走5米,再向东走3米,两次一共向东走了多少米?+5+3+8(+5)+(+3)= +8 (2)向东走-5米,再向东走-3米,两次一共向东走了多少米? 同向情况:-3-5-8(-5)+(-3)= -8 结论:同号两数相加,取相同的符号,并把绝对值相加。 异向情况:(3)向东走5米,再向东走-3米,两次一共向东走了多少米? +2(+5)+(-3)= +2 +5-3(4)向东走-5米,再向东走3米,两次一共向东走了多少米? +3-5-2(-5)+(+3)= -2 结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。 问题2:在东西走向的马路上,小明从O点出发,向东走5米,再向东走
-5米,两次一共向东走了多少米? 问题3:在东西走向的马路上,小明从O点出发,向东走-5米,再向东走0米,两次一共向东走了多少米? (+5)+(-5)= 0 +5-5结论:互为相反数的两个数相加得零。 结论:一个数同零相加,仍得这个数。 -5(-5)+ 0 = -5 有理数加法法则
1.同号两数相加,取相同的符号,并把绝对值相加。
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。 互为相反数的两个数相加得0。
3.一个数同0相加,仍得这个数。三、分析特征 强化理解 总结步骤 ( - 4 ) + ( - 8 ) = -( 4 + 8 )= -12
↓ ↓ ↓
同号两数相加 取相同符号 通过绝对值化归
为算术数的加法
( - 9 ) + (+ 2) = -( 9 -2) = -7
↓ ↓ ↓
异号两数相加 取绝对值较大 通过绝对值化归
的加数的符号 为算术数的减法
同号两数之和——这是名符其实的和,做加法。
异号两数之和——表面上叫“和”,其实是做减法。 有理数中的“和”与小学算术中 “和”的比较结果 类型 结论:在有理数运算中,算术中的某些结论不一定再成立。 四、对比异同 强化记忆 五、设置问题 强化关键
判断正误并改错
(1)两个负数相加,绝对值相减;
(2)正数加负数,和为负数;
(3)负数加正数,和为正数;
(4)两个有理数的和为负数时,这 两个有理数都是负数。
六、应用举例 巩固练习 例题:计算下列各题(1) ( -6 ) + ( -8 ) ; (2) 5.2 + (- 4.5) ; (3) +练习1:口算下列各题,并说理由
(1)(+4)+(+7);(2)(-4)+(-7);(3)(+4)+(-7);
(4)(-4)+(+7) ;(5)(+4)+(-4);(6)(+9)+(-2);(7)(-9)+(+2);(8)(-9)+0练习2:
1)计算:
(1)15+(-22);(2)(-0.9)+1.5;(3)2.7+(-3.5)
2)用“>”或“<”填空:
(1)如果a>0,b>0,那么a+b____0;
(2) 如果a<0,b<0,那么a+b____0;
(3) 如果a>0,b<0,|a|>|b|,那么a+b____0;
(4) 如果a<0,b>0, |a|<|b|,那么a+b____0;七、课程小结 布置作业 小结 (1)本节课所学习的主要内容;
(2)运用有理数加法法则的关键问题;
(3)本节课涉及的数学思想方法。
一、复习提问
1、下列各组数中,哪一个数的绝对值大?
(1)7和4; (2)-7和4; (3)7和-4; (4)-7和-4。
2、说明下列用负数表示的量的实际意义
(1)小兰第一次前进了5米,接着按同一方向又前进了-2米;
(2)北京的气温第一天上升了3℃,第二天又上升了-1℃;
(3)东方汽车向东走了4千米之后,再向东走了-2千米。
3、根据上述问题,回答
(1)小兰两次一共前进了几米?
(2)北京的气温两天一共上升了几度?
(3)东方汽车一共向东走了几千米?
二、动态演示 分类归纳 总结法则问题1:在东西走向的马路上,小明从O点出发,第一次走5米,第二次继续走3米,问小明两次一共向东走多少米?
(1)向东走5米,再向东走3米,两次一共向东走了多少米?+5+3+8(+5)+(+3)= +8 (2)向东走-5米,再向东走-3米,两次一共向东走了多少米? 同向情况:-3-5-8(-5)+(-3)= -8 结论:同号两数相加,取相同的符号,并把绝对值相加。 异向情况:(3)向东走5米,再向东走-3米,两次一共向东走了多少米? +2(+5)+(-3)= +2 +5-3(4)向东走-5米,再向东走3米,两次一共向东走了多少米? +3-5-2(-5)+(+3)= -2 结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。 问题2:在东西走向的马路上,小明从O点出发,向东走5米,再向东走
-5米,两次一共向东走了多少米? 问题3:在东西走向的马路上,小明从O点出发,向东走-5米,再向东走0米,两次一共向东走了多少米? (+5)+(-5)= 0 +5-5结论:互为相反数的两个数相加得零。 结论:一个数同零相加,仍得这个数。 -5(-5)+ 0 = -5 有理数加法法则
1.同号两数相加,取相同的符号,并把绝对值相加。
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。 互为相反数的两个数相加得0。
3.一个数同0相加,仍得这个数。三、分析特征 强化理解 总结步骤 ( - 4 ) + ( - 8 ) = -( 4 + 8 )= -12
↓ ↓ ↓
同号两数相加 取相同符号 通过绝对值化归
为算术数的加法
( - 9 ) + (+ 2) = -( 9 -2) = -7
↓ ↓ ↓
异号两数相加 取绝对值较大 通过绝对值化归
的加数的符号 为算术数的减法
同号两数之和——这是名符其实的和,做加法。
异号两数之和——表面上叫“和”,其实是做减法。 有理数中的“和”与小学算术中 “和”的比较结果 类型 结论:在有理数运算中,算术中的某些结论不一定再成立。 四、对比异同 强化记忆 五、设置问题 强化关键
判断正误并改错
(1)两个负数相加,绝对值相减;
(2)正数加负数,和为负数;
(3)负数加正数,和为正数;
(4)两个有理数的和为负数时,这 两个有理数都是负数。
六、应用举例 巩固练习 例题:计算下列各题(1) ( -6 ) + ( -8 ) ; (2) 5.2 + (- 4.5) ; (3) +练习1:口算下列各题,并说理由
(1)(+4)+(+7);(2)(-4)+(-7);(3)(+4)+(-7);
(4)(-4)+(+7) ;(5)(+4)+(-4);(6)(+9)+(-2);(7)(-9)+(+2);(8)(-9)+0练习2:
1)计算:
(1)15+(-22);(2)(-0.9)+1.5;(3)2.7+(-3.5)
2)用“>”或“<”填空:
(1)如果a>0,b>0,那么a+b____0;
(2) 如果a<0,b<0,那么a+b____0;
(3) 如果a>0,b<0,|a|>|b|,那么a+b____0;
(4) 如果a<0,b>0, |a|<|b|,那么a+b____0;七、课程小结 布置作业 小结 (1)本节课所学习的主要内容;
(2)运用有理数加法法则的关键问题;
(3)本节课涉及的数学思想方法。
