2.7有理数的乘法课件
图片预览





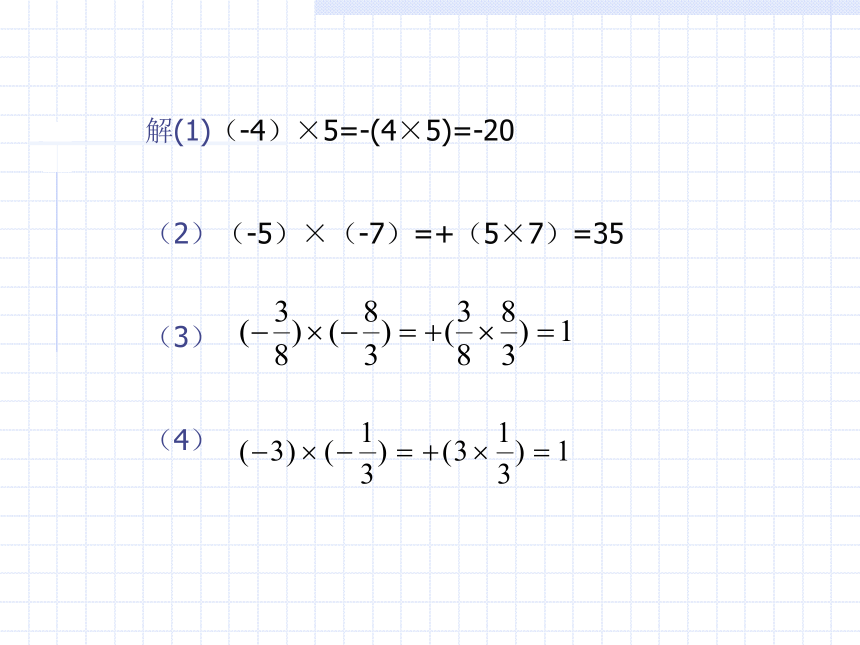
文档简介
课件15张PPT。义务教育课程标准实验教科书(鲁教版)六年级 上册 第二章有理数及其运算7有理数的乘法
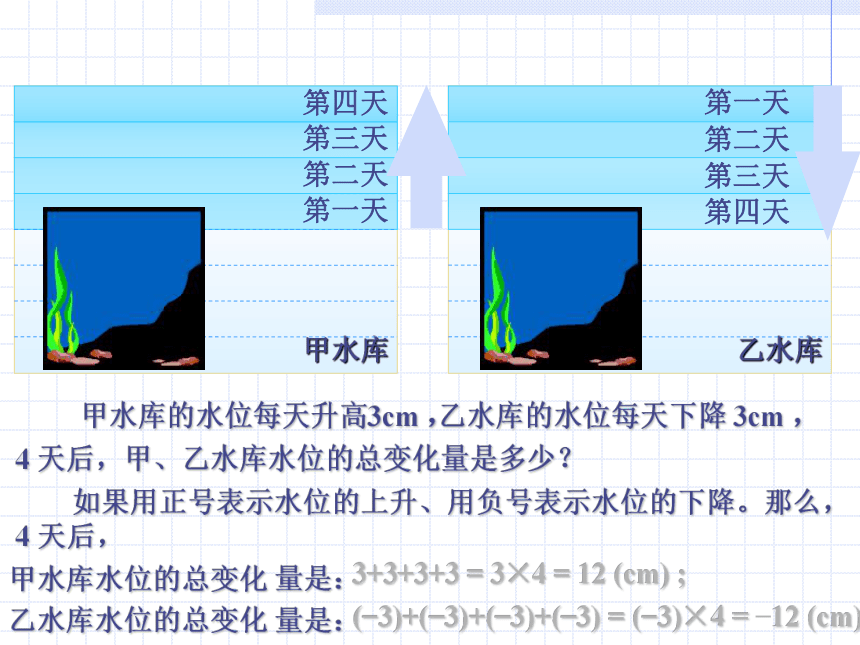
甲水库第一天
乙水库甲水库的水位每天升高3cm ,第二天第三天第四天乙水库的水位每天下降 3cm , 第一天 第二天 第三天 第四天4 天后,甲、乙水库水位的总变化量是多少? 如果用正号表示水位的上升、用负号表示水位的下降。那么,4 天后,甲水库水位的总变化 量是:
乙水库水位的总变化 量是:3+3+3+3 = 3×4 = 12 (cm) ;(?3)+(?3)+(?3)+(?3) = (?3)×4 = ?12 (cm) ;(?3)×4 = ?12(?3)×3 = ,(?3)×2 = ,(?3)×1 = ,(?3)×0 = ,?9?6?30(?3)×(?1) = ,
(?3)×(?2) = ,
(?3)×(?3) = ,
(?3)×(?4) = ,第二个因数减少 1 时,积 怎么变化?36912议一议猜一猜任何数与零相乘,积仍为零。有理数乘法法则两数相乘,
同号得正,异号得负,
并把它们的绝对值相乘。注意:“同号得正”中正数乘以正数得正数就是小学学习的乘法,有理数中特别注意“负负得正”和“异号得负”?如何应用乘法法则:用有理数乘法法则与小学学习的乘法相比,由于引入了负数,故符号一旦确定,就归结为小学的乘法了。?因此,在进行有理数乘法运算时更需时时注意:先确定符号再确定绝对值。? 例 题 分 析例1 计算:
(1) (?4)×5 ; (2) (?4)×(?7) ;(3) (4)提示:求解中的步骤
第一步是确定积的符号;
第二步是 确定积的绝对值。解(1)(-4)×5=-(4×5)=-20
(2)(-5)×(-7)=+(5×7)=35
(3)
(4)解题后的反思由例 1 的 (3) 、(4) 求解可知,
乘积为1的两个有理数互为倒数。
想一想:三个有理数相乘,你会计算吗?
例2 计算:
(1) (-4)×5×(-0.25)
(2) 解: (1)原式=[-(4×5)]×(-0.25)
= (-20)×(-0.25)
= +(20×0.25)
=5
(2)原式=方法提示:三个有理数相乘,先把前两个数相乘,再把所得结果与另一数相乘。
几个有理数相乘,因数都不为 0 时,
积的符号怎样确定? 有一因数为 0 时,积是多少?
几个不等于零的数相乘,积的符号由负因数的个数决定。
当负因数有奇数个时,积为负;
当负因数有偶数个时,积为正。议一议:小结与思考1、本节课你最大的收获是什么?
2、有理数的乘法与小学的(正数)的乘法有什么联系和不同点?
3、小学所学的乘法的有关运算律及相关技巧能否用到有理数的乘法中来?1、如果-5x是正数,那么x的符号是( ) A. X>0 B. X≥0 C. X<0 D. X≤02、若a·b=0,则 ( ) A. a = 0 B. a = 0或b = 0
C. b = 0 D. a = 0且b = 03 、两个有理数的积是负数,则这两个数之和是( )正数 B. 负数
C. 零 D. 以上三种情况都有可能课 堂 练 习4.口答:
(1) 6×(-9); ? (2) (-6)×(-9);?
(3) (-6)×9; (4) (-6)×1;
(5) (-6)×(-1); (6) 6×(-1);?
(7) (-6)×0;? (8) 0×(-6);
-5454-54-66-6005.填空:
(1) 2×(-6)=______;(2) 2+(-6)=_______;
(3) (-2)×6=________;(4) (-2)+6=______;
(5) (-2)×(-6)=______;(6) (-2)+(-6)=_____;
(9) |-7|×|-3|=_______;(10) (-7)×(-3)=______.
-12-4-12412-821216.计算:
(1) (-16)×15;??? (2) (-9)×(-14);??????
?
(3) (-36)×(-1); (4) 13×(-11);???????
?
(5) (-25)×16;?? (6) (-10)×(-16).
甲水库第一天
乙水库甲水库的水位每天升高3cm ,第二天第三天第四天乙水库的水位每天下降 3cm , 第一天 第二天 第三天 第四天4 天后,甲、乙水库水位的总变化量是多少? 如果用正号表示水位的上升、用负号表示水位的下降。那么,4 天后,甲水库水位的总变化 量是:
乙水库水位的总变化 量是:3+3+3+3 = 3×4 = 12 (cm) ;(?3)+(?3)+(?3)+(?3) = (?3)×4 = ?12 (cm) ;(?3)×4 = ?12(?3)×3 = ,(?3)×2 = ,(?3)×1 = ,(?3)×0 = ,?9?6?30(?3)×(?1) = ,
(?3)×(?2) = ,
(?3)×(?3) = ,
(?3)×(?4) = ,第二个因数减少 1 时,积 怎么变化?36912议一议猜一猜任何数与零相乘,积仍为零。有理数乘法法则两数相乘,
同号得正,异号得负,
并把它们的绝对值相乘。注意:“同号得正”中正数乘以正数得正数就是小学学习的乘法,有理数中特别注意“负负得正”和“异号得负”?如何应用乘法法则:用有理数乘法法则与小学学习的乘法相比,由于引入了负数,故符号一旦确定,就归结为小学的乘法了。?因此,在进行有理数乘法运算时更需时时注意:先确定符号再确定绝对值。? 例 题 分 析例1 计算:
(1) (?4)×5 ; (2) (?4)×(?7) ;(3) (4)提示:求解中的步骤
第一步是确定积的符号;
第二步是 确定积的绝对值。解(1)(-4)×5=-(4×5)=-20
(2)(-5)×(-7)=+(5×7)=35
(3)
(4)解题后的反思由例 1 的 (3) 、(4) 求解可知,
乘积为1的两个有理数互为倒数。
想一想:三个有理数相乘,你会计算吗?
例2 计算:
(1) (-4)×5×(-0.25)
(2) 解: (1)原式=[-(4×5)]×(-0.25)
= (-20)×(-0.25)
= +(20×0.25)
=5
(2)原式=方法提示:三个有理数相乘,先把前两个数相乘,再把所得结果与另一数相乘。
几个有理数相乘,因数都不为 0 时,
积的符号怎样确定? 有一因数为 0 时,积是多少?
几个不等于零的数相乘,积的符号由负因数的个数决定。
当负因数有奇数个时,积为负;
当负因数有偶数个时,积为正。议一议:小结与思考1、本节课你最大的收获是什么?
2、有理数的乘法与小学的(正数)的乘法有什么联系和不同点?
3、小学所学的乘法的有关运算律及相关技巧能否用到有理数的乘法中来?1、如果-5x是正数,那么x的符号是( ) A. X>0 B. X≥0 C. X<0 D. X≤02、若a·b=0,则 ( ) A. a = 0 B. a = 0或b = 0
C. b = 0 D. a = 0且b = 03 、两个有理数的积是负数,则这两个数之和是( )正数 B. 负数
C. 零 D. 以上三种情况都有可能课 堂 练 习4.口答:
(1) 6×(-9); ? (2) (-6)×(-9);?
(3) (-6)×9; (4) (-6)×1;
(5) (-6)×(-1); (6) 6×(-1);?
(7) (-6)×0;? (8) 0×(-6);
-5454-54-66-6005.填空:
(1) 2×(-6)=______;(2) 2+(-6)=_______;
(3) (-2)×6=________;(4) (-2)+6=______;
(5) (-2)×(-6)=______;(6) (-2)+(-6)=_____;
(9) |-7|×|-3|=_______;(10) (-7)×(-3)=______.
-12-4-12412-821216.计算:
(1) (-16)×15;??? (2) (-9)×(-14);??????
?
(3) (-36)×(-1); (4) 13×(-11);???????
?
(5) (-25)×16;?? (6) (-10)×(-16).
