平均变化率
图片预览








文档简介
课件21张PPT。平均变化率南京外国语学校严青苏教版选修2-2《导数及其应用》平均变化率第一课时Yanqing29@yahoo.com.cn生活 数学 活动 思考 《导数及其应用》在整个高中教材中的地位和作用是非常重要的,它既是对函数知识的补充和完善,也为今后进一步学习微积分奠定基础。通过本章的学习,促进学生全面认识数学的价值(应用价值、科学价值、文化价值),使学生对变量数学的思想方法有新的感悟,从而进一步发展学生的数学思维能力。 新课标对“导数及其应用”内容的处理有了较大的变化,它不介绍极限的形式化定义及相关知识,也有别于以往教材将导数仅仅作为一种特殊的极限、一种“规则”来学习的处理方式,而是按照:平均变化率—瞬时变化率—导数的概念—导数的几何意义这样的顺序来安排,用“逼近”的方法定义导数,这种概念建立的方式形象、直观、生动又容易理解,突出了导数概念的本质。平均变化率是本章的一个重要的基本概念,本节课是《导数及其应用》的起始课,对导数概念的形成起着奠基作用。 情感、态度、价值观 感受数学模型在刻画客观世界中的作用,进一步
领会变量数学的思想方法,提高能力。过程与方法 通过丰富的实例,让学生经历平均变化率概念的形成过程,
体会平均变化率是刻画变量变化快慢程度的一种数学模型;知识与技能 理解平均变化率的概念,了解平均变化率的几何意义,
会计算函数在某个区间上的平均变化率;平均变化率概念及其形成过程 启发式教学与探究式学习相结合。
通过生活中的实例,引导学生分析和归纳,让学生在已
有认知结构的基础上建构新知识,从而达到概念的自然
形成,进而从数学的外部到数学的内部,启发学生运用
概念探究新问题。这样学生不会感到突兀,并能进一步
感受到数学来源于生活,生活中处处蕴含着数学化的知
识,同时可以提高他们学习数学的主观能动性。教师在
教学中应遵循五“W”原则(who,what,why when,
how),尤其要关注其中的三个原则,即 “谁在学?为什
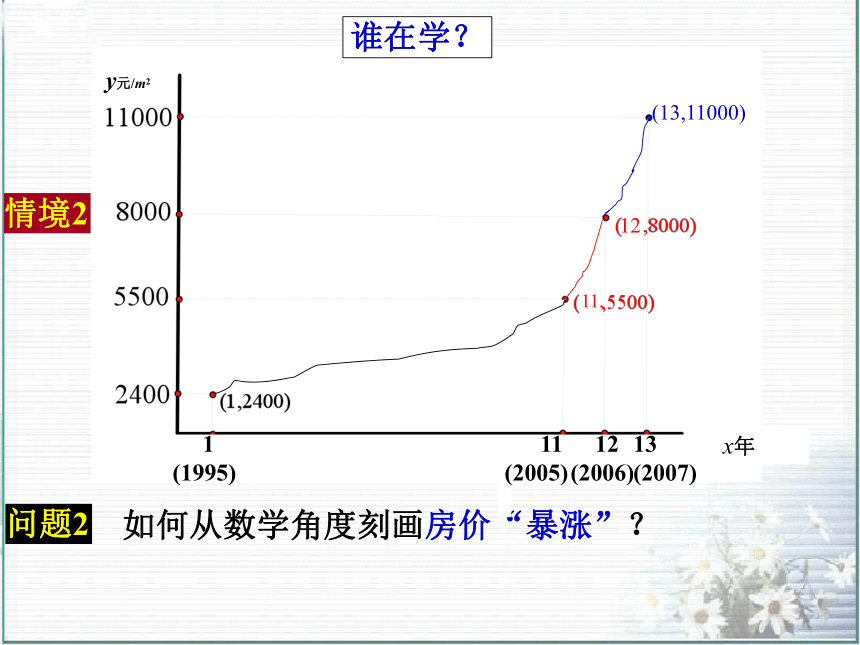
么要学?怎么学?”利用多媒体辅助教学,突出重点、突破难点,提高效率.为什么要学?必要性谁在学?怎么学?学什么?学生的现实概念课教学主线概念概念内涵、外延几何意义实际意义 问题情境数学模型应用拓展关注问题知识,能力认知水平,情境1如何从数学角度刻画2002年至2006年这4年我国
人均GDP “猛增”? 问题1 如何从数学角度刻画房价“暴涨”?情境2问题2谁在学?如何从数学角度刻画股指“跳水”?问题3如何从数学角度刻画气温“陡升”? 情境4问题4 用怎样的数学模型刻画函数值变化的快慢程度?问题5 通过GDP“猛增”、房价“暴涨”、股指“跳水”、气温“陡升”
等贴近学生、贴近生活、贴近教材的实例,让学生感知客
观世界中存在着变化快慢不同的现象,让学生在已有认知
结构的基础上建构新知识,从而达到概念的自然形成,这
样学生不会感到突兀,并能进一步感受到数学来源于生活,
生活中处处蕴含着数学化的知识,从而探究得到用平均变
化率来刻画这种快慢程度。函数 f (x) 在区间[x1,x2]上的平均变化率为你能给出
函数 f (x) 在区间[x1,x2]上的平均变化率的定义吗?平均变化率有什么几何意义呢?思考1思考2由特殊到一般给出函数 f (x)的平均变化率的定义,
并了解它的几何意义。 甲乙两人投入相同资金经营同一种商品,甲用5年时间挣到10万元,乙用5个月时间挣到2万元.你能评价甲、乙两人的经营成果吗?为什么 ? 甲乙两人经营同一种商品,甲挣到10万元,乙挣到2万元,你能评价甲、乙两人的经营成果吗?为什么?你能举出生活中与平均变化率有关的例子吗? 活动1活动2模型解释丰富对模型的认识启发学生运用 概念探究新问题,提高学习数学的主观能动性。例1 某婴儿从出生到第12个月的体重变化如图所示,分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率.规范 ; 感悟例2 已知函数f (x) =2x+1、g(x) =-2x, 分别计算在区间 [-3, -1]、[0, 5] f (x)及 g (x)的平均变化率. 一次函数y =kx+b(k≠0)在区间[m,n]上的平均变化率
有什么特点?想一想算 ; 几何意义通过学生活动和例题讲解,由数学外部到数学内部,从模仿举例、尝试探究到拓展应用,使学生加深对平均变化率概念的认识。(1)[1, 3];
(2)[1, 2];
(3)[1, 1.1];
(4)[1, 1.001];
(5)[1, 1.0001]; 一运动质点的位移S与时间t满足S(t)=t2,分别计算S(t)在下列区间上的平均变化率.(位移单位为m,时间单位为s) 432.12.0011.9991.991.92(6)[0.999, 1];
(7)[0.99, 1];
(8)[0.9, 1].2.0001练一练 如何刻画t=1这一时刻质点运动的快慢程度呢? 思考3由区间长度的缩小,通过计算从数的角度观察相应的平均变化率变化的趋势,通过几何画板的演示,从形的角度进一步感悟变量数学的思想,通过逼近的思想方法为瞬时变化率的学习作好铺垫,达到承上启下的作用。2.我想进一步探究的问题是——1.这节课我的收获是——3.这节课我最感兴趣的地方是——通过开放式小结,使学生学会学习,培养学习的主动性。1.必做题2.选做题3.思考题布置作业第7页2,3题我们都吹过气球回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢。从数学角度,如何描述这种现象呢? 一运动质点的位移S与时间t满足S(t)=t2, 如何刻画t=1这一时刻质点运动变化的快慢程度呢? (位移单位为m, 时间单位为s) 作业:必做题、选做题、拓展题,分层教学,因材施教。
通过师生交流 、学生活动及时了解学生的学习状况;通过4个情境、3个思考、2个活动、2个例题、1个练习构成
一个及时反馈的学习体系,不断调整和改善学生的学习进程。 谢谢!yanqing29@yahoo.com.cn
领会变量数学的思想方法,提高能力。过程与方法 通过丰富的实例,让学生经历平均变化率概念的形成过程,
体会平均变化率是刻画变量变化快慢程度的一种数学模型;知识与技能 理解平均变化率的概念,了解平均变化率的几何意义,
会计算函数在某个区间上的平均变化率;平均变化率概念及其形成过程 启发式教学与探究式学习相结合。
通过生活中的实例,引导学生分析和归纳,让学生在已
有认知结构的基础上建构新知识,从而达到概念的自然
形成,进而从数学的外部到数学的内部,启发学生运用
概念探究新问题。这样学生不会感到突兀,并能进一步
感受到数学来源于生活,生活中处处蕴含着数学化的知
识,同时可以提高他们学习数学的主观能动性。教师在
教学中应遵循五“W”原则(who,what,why when,
how),尤其要关注其中的三个原则,即 “谁在学?为什
么要学?怎么学?”利用多媒体辅助教学,突出重点、突破难点,提高效率.为什么要学?必要性谁在学?怎么学?学什么?学生的现实概念课教学主线概念概念内涵、外延几何意义实际意义 问题情境数学模型应用拓展关注问题知识,能力认知水平,情境1如何从数学角度刻画2002年至2006年这4年我国
人均GDP “猛增”? 问题1 如何从数学角度刻画房价“暴涨”?情境2问题2谁在学?如何从数学角度刻画股指“跳水”?问题3如何从数学角度刻画气温“陡升”? 情境4问题4 用怎样的数学模型刻画函数值变化的快慢程度?问题5 通过GDP“猛增”、房价“暴涨”、股指“跳水”、气温“陡升”
等贴近学生、贴近生活、贴近教材的实例,让学生感知客
观世界中存在着变化快慢不同的现象,让学生在已有认知
结构的基础上建构新知识,从而达到概念的自然形成,这
样学生不会感到突兀,并能进一步感受到数学来源于生活,
生活中处处蕴含着数学化的知识,从而探究得到用平均变
化率来刻画这种快慢程度。函数 f (x) 在区间[x1,x2]上的平均变化率为你能给出
函数 f (x) 在区间[x1,x2]上的平均变化率的定义吗?平均变化率有什么几何意义呢?思考1思考2由特殊到一般给出函数 f (x)的平均变化率的定义,
并了解它的几何意义。 甲乙两人投入相同资金经营同一种商品,甲用5年时间挣到10万元,乙用5个月时间挣到2万元.你能评价甲、乙两人的经营成果吗?为什么 ? 甲乙两人经营同一种商品,甲挣到10万元,乙挣到2万元,你能评价甲、乙两人的经营成果吗?为什么?你能举出生活中与平均变化率有关的例子吗? 活动1活动2模型解释丰富对模型的认识启发学生运用 概念探究新问题,提高学习数学的主观能动性。例1 某婴儿从出生到第12个月的体重变化如图所示,分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率.规范 ; 感悟例2 已知函数f (x) =2x+1、g(x) =-2x, 分别计算在区间 [-3, -1]、[0, 5] f (x)及 g (x)的平均变化率. 一次函数y =kx+b(k≠0)在区间[m,n]上的平均变化率
有什么特点?想一想算 ; 几何意义通过学生活动和例题讲解,由数学外部到数学内部,从模仿举例、尝试探究到拓展应用,使学生加深对平均变化率概念的认识。(1)[1, 3];
(2)[1, 2];
(3)[1, 1.1];
(4)[1, 1.001];
(5)[1, 1.0001]; 一运动质点的位移S与时间t满足S(t)=t2,分别计算S(t)在下列区间上的平均变化率.(位移单位为m,时间单位为s) 432.12.0011.9991.991.92(6)[0.999, 1];
(7)[0.99, 1];
(8)[0.9, 1].2.0001练一练 如何刻画t=1这一时刻质点运动的快慢程度呢? 思考3由区间长度的缩小,通过计算从数的角度观察相应的平均变化率变化的趋势,通过几何画板的演示,从形的角度进一步感悟变量数学的思想,通过逼近的思想方法为瞬时变化率的学习作好铺垫,达到承上启下的作用。2.我想进一步探究的问题是——1.这节课我的收获是——3.这节课我最感兴趣的地方是——通过开放式小结,使学生学会学习,培养学习的主动性。1.必做题2.选做题3.思考题布置作业第7页2,3题我们都吹过气球回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢。从数学角度,如何描述这种现象呢? 一运动质点的位移S与时间t满足S(t)=t2, 如何刻画t=1这一时刻质点运动变化的快慢程度呢? (位移单位为m, 时间单位为s) 作业:必做题、选做题、拓展题,分层教学,因材施教。
通过师生交流 、学生活动及时了解学生的学习状况;通过4个情境、3个思考、2个活动、2个例题、1个练习构成
一个及时反馈的学习体系,不断调整和改善学生的学习进程。 谢谢!yanqing29@yahoo.com.cn
