2。2。3向量的数乘运算(兰溪)
文档属性
| 名称 | 2。2。3向量的数乘运算(兰溪) |

|
|
| 格式 | rar | ||
| 文件大小 | 460.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-26 00:00:00 | ||
图片预览


文档简介
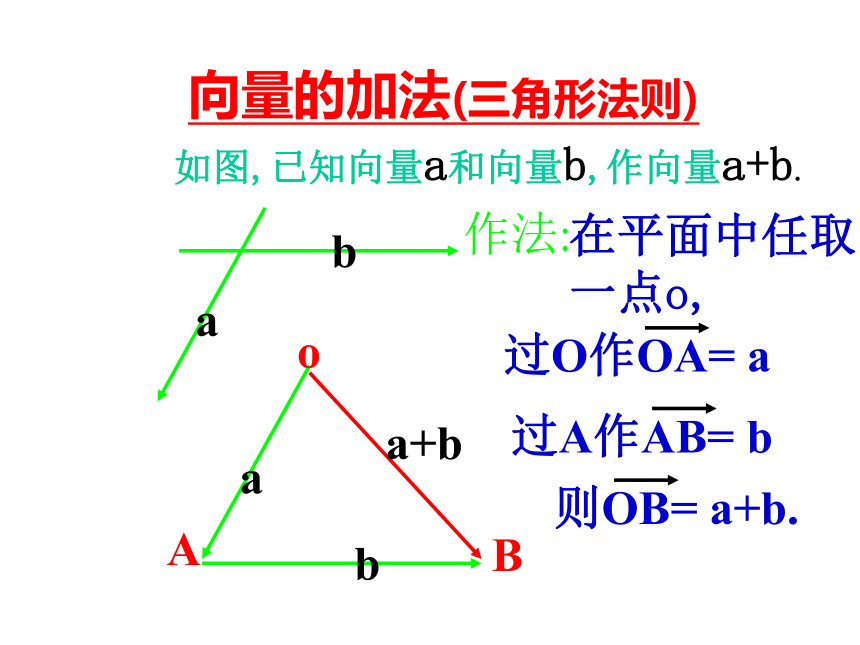
课件18张PPT。2.2.3向量的数乘运算向量的加法(三角形法则)如图,已知向量a和向量b,作向量a+b.作法:在平面中任取
一点o,o例题讲解小结回顾引入练习
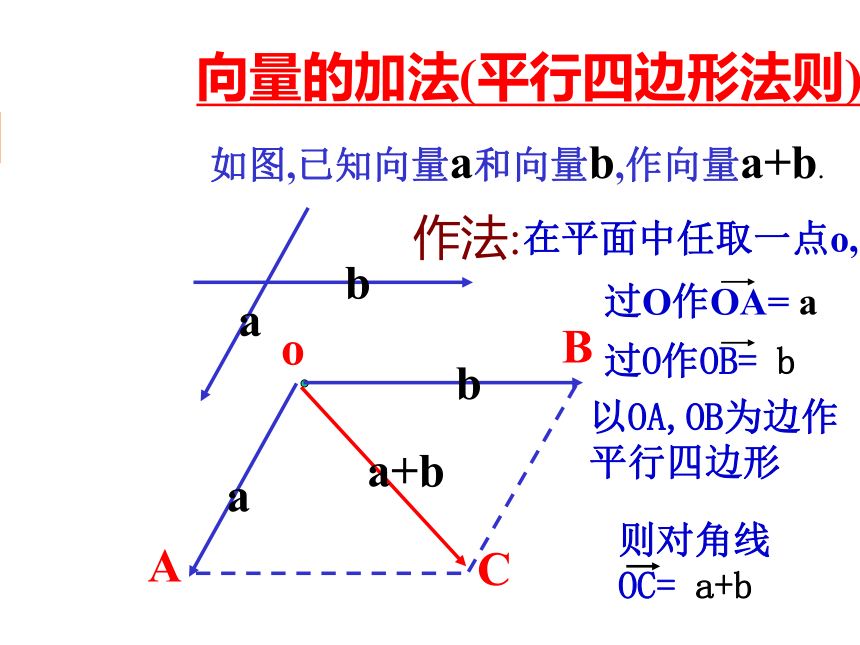
新课讲解定理讲解课堂练习向量的加法(平行四边形法则)如图,已知向量a和向量b,作向量a+b.作法:b以OA,OB为边作
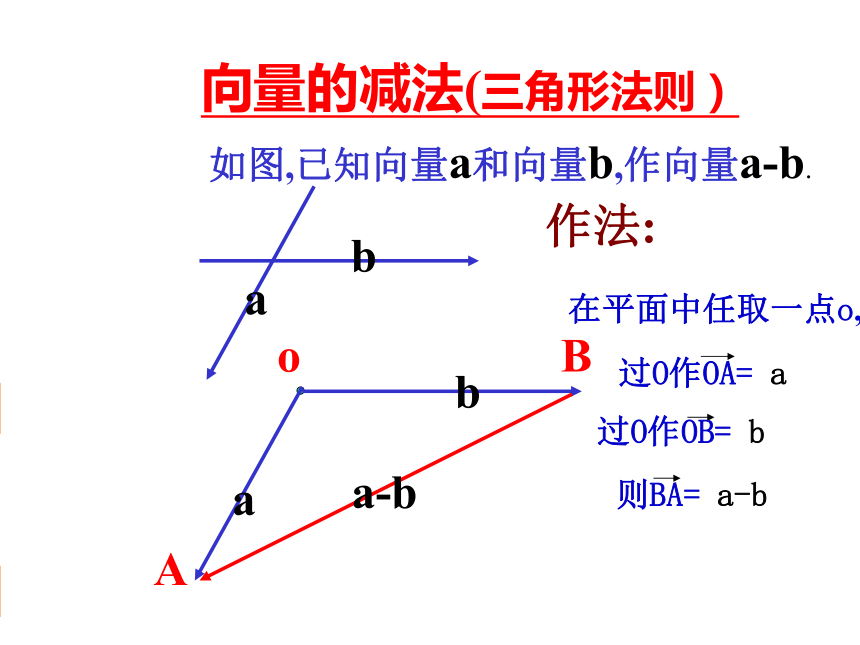
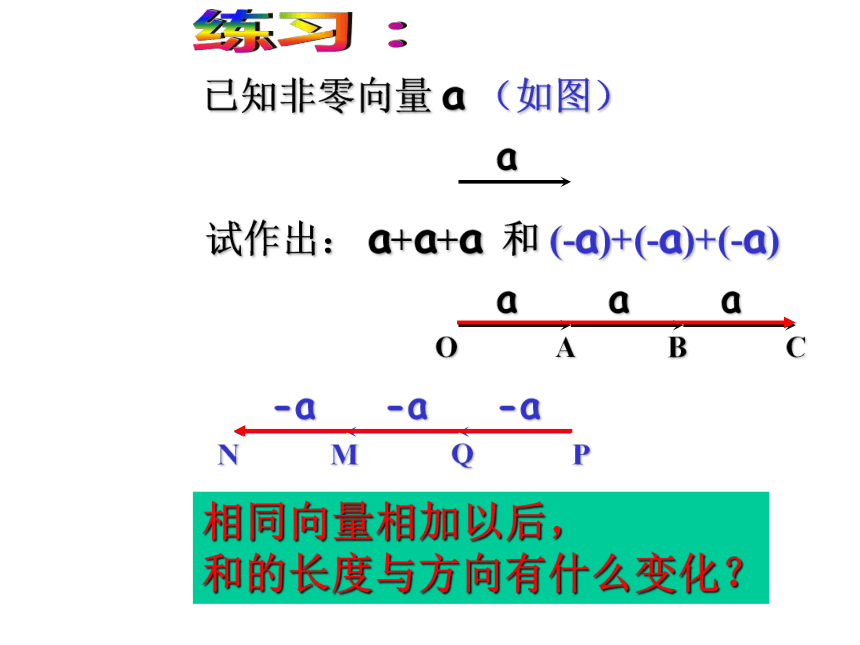
平行四边形 复 习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习向量的减法(三角形法则)如图,已知向量a和向量b,作向量a-b.b作法:在平面中任取一点o, 复 习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习相同向量相加以后,
和的长度与方向有什么变化?定义:一般地,实数λ与向量a的积是一个向量,
这种运算叫做向量的数乘运算,记作λa,
它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
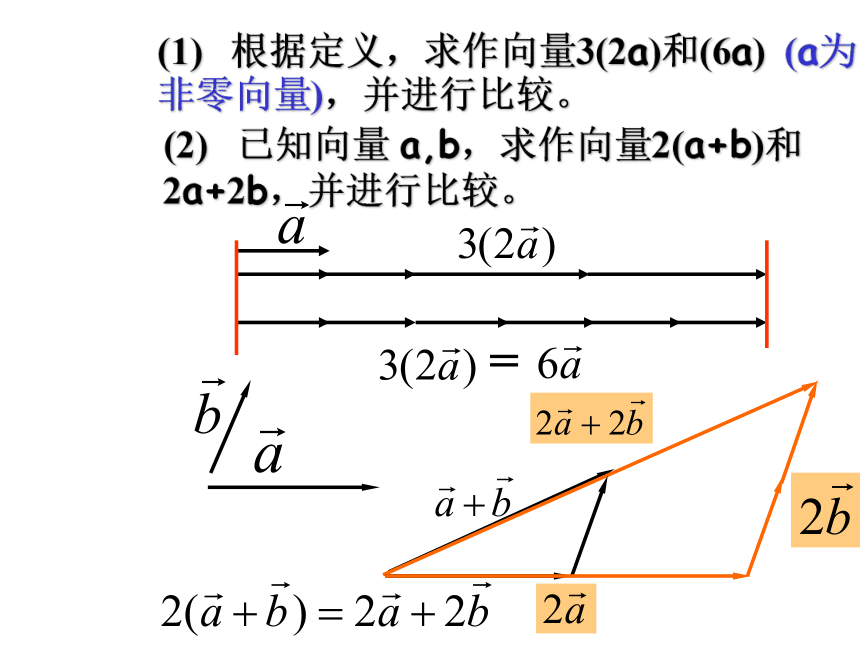
特别地,当λ=0或a=0时, λa=0(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。(2) 已知向量 a,b,求作向量2(a+b)和2a+2b,并进行比较。 例1 计算:
(1) (-3)×4a
(2) 3(a+b) –2(a-b)-a
(3) (2a+3b-c) –(3a-2b+c)-12a5b-a+5b-2c思考?引入向量数乘运算后,你能发现数乘向量与原向量之间的位置关系吗?共线向量的条件:对于向量 a (a≠0), b ,以及实数λ问题1:如果 b=λa ,
那么,向量a与b是否共线?问题2:如果 向量a与b共线
那么,b=λa ?定理:向量 b 与非零向量 a 共线当且仅当
有且只有一个实数λ,使得 b=λa 定理:向量 b 与非零向量 a 共线当且仅当
有且只有一个实数λ,使得 b=λa 几何画板练习题:作业布置:A p54-55
一点o,o例题讲解小结回顾引入练习
新课讲解定理讲解课堂练习向量的加法(平行四边形法则)如图,已知向量a和向量b,作向量a+b.作法:b以OA,OB为边作
平行四边形 复 习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习向量的减法(三角形法则)如图,已知向量a和向量b,作向量a-b.b作法:在平面中任取一点o, 复 习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习相同向量相加以后,
和的长度与方向有什么变化?定义:一般地,实数λ与向量a的积是一个向量,
这种运算叫做向量的数乘运算,记作λa,
它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0或a=0时, λa=0(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。(2) 已知向量 a,b,求作向量2(a+b)和2a+2b,并进行比较。 例1 计算:
(1) (-3)×4a
(2) 3(a+b) –2(a-b)-a
(3) (2a+3b-c) –(3a-2b+c)-12a5b-a+5b-2c思考?引入向量数乘运算后,你能发现数乘向量与原向量之间的位置关系吗?共线向量的条件:对于向量 a (a≠0), b ,以及实数λ问题1:如果 b=λa ,
那么,向量a与b是否共线?问题2:如果 向量a与b共线
那么,b=λa ?定理:向量 b 与非零向量 a 共线当且仅当
有且只有一个实数λ,使得 b=λa 定理:向量 b 与非零向量 a 共线当且仅当
有且只有一个实数λ,使得 b=λa 几何画板练习题:作业布置:A p54-55
