人教版数学八年级下册17.1勾股定理 优质课课件(共28张PPT)
文档属性
| 名称 | 人教版数学八年级下册17.1勾股定理 优质课课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-20 00:00:00 | ||
图片预览



文档简介
(共28张PPT)
17.1探究勾股定理
茫茫宇宙,浩瀚太空,如果有一天,我们真的和外星人相遇了,该用什么语言与他交流呢?曾经有科学家认为,用两个图形作为与外星人交谈的媒介,其中一个就是“数形关系”(勾股定理)。因为这种自然图形所具备的“数形关系”在整个宇宙中是普遍存在的。
学习目标
1.了解勾股定理的内容,并掌握直角三角形三边之间的数量关系。(重点)
2.能够运用勾股定理进行简单的计算。
(难点)
2500年前,古希腊著名数学家毕达哥拉斯非常善于观察和思考,经常能从平淡的生活现象中发现数学问题.
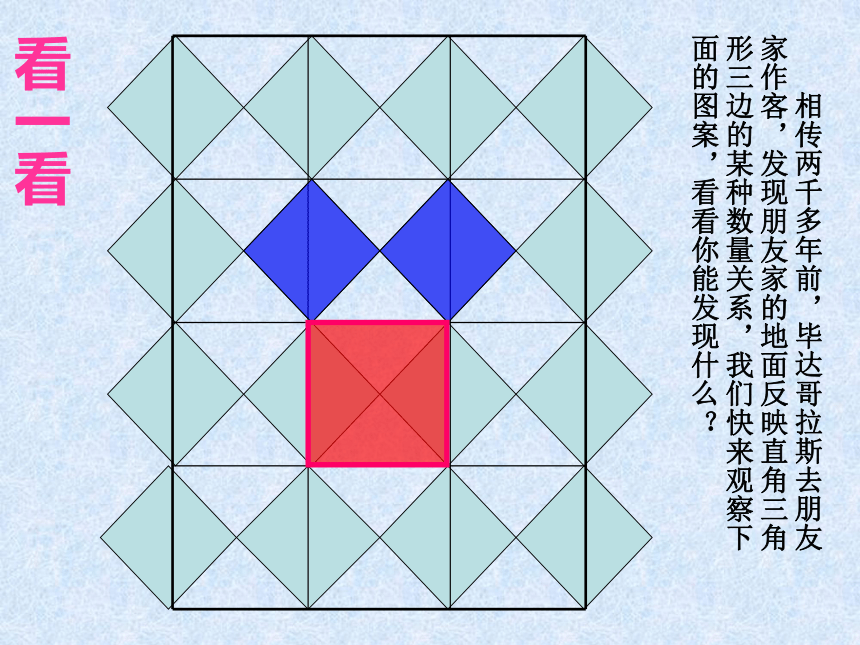
看一看
相传两千多年前,毕达哥拉斯去朋友家作客,发现朋友家的地面反映直角三角形三边的某种数量关系,我们快来观察下面的图案,看看你能发现什么?
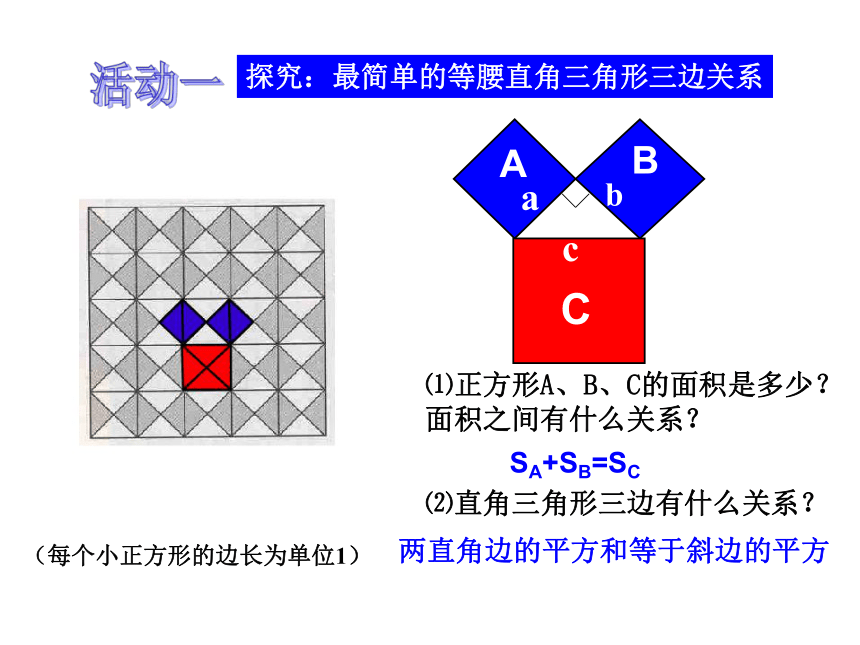
⑴正方形A、B、C的面积是多少?面积之间有什么关系?
⑵直角三角形三边有什么关系?
SA+SB=SC
两直角边的平方和等于斜边的平方
探究:最简单的等腰直角三角形三边关系
活动一
A
B
C
(每个小正方形的边长为单位1)
a
c
b
A
B
C
A
B
C
(每个小正方形的边长为单位1)
图2-1
图2-2
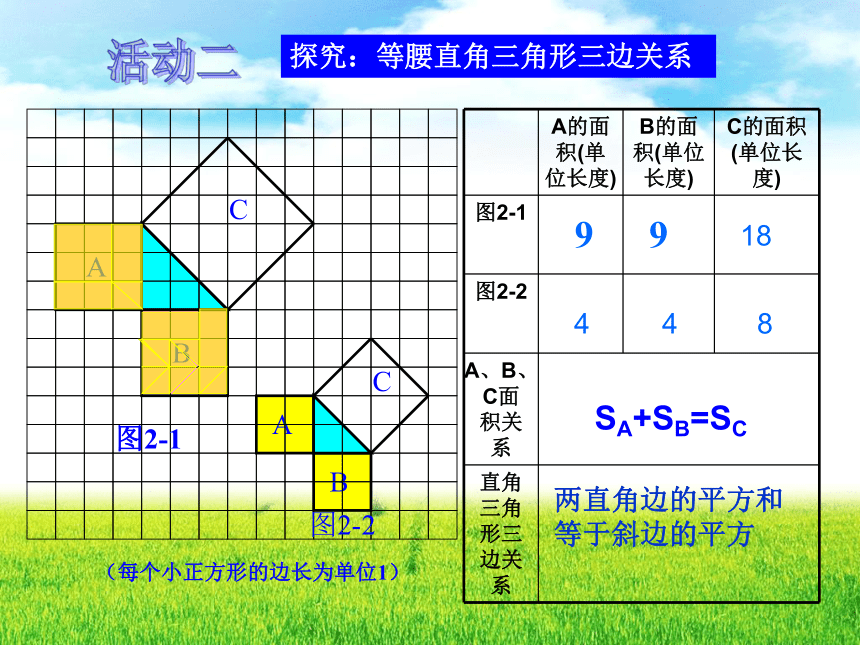
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2-1
图2-2
A、B、C面积关系 直角三角形三边关系
探究:等腰直角三角形三边关系
活动二
9
9
18
4
4
两直角边的平方和
等于斜边的平方
SA+SB=SC
8
C
A
B
a
b
c
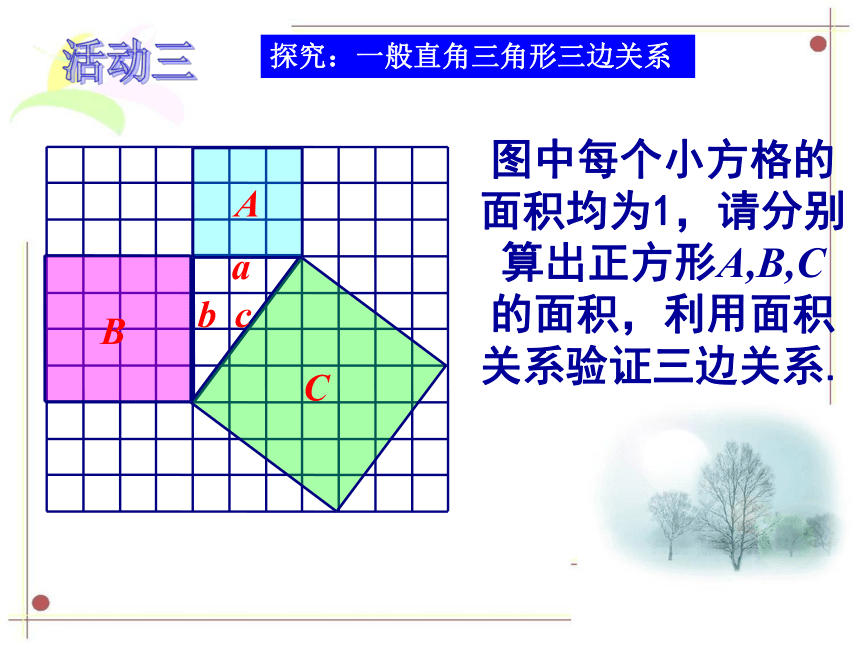
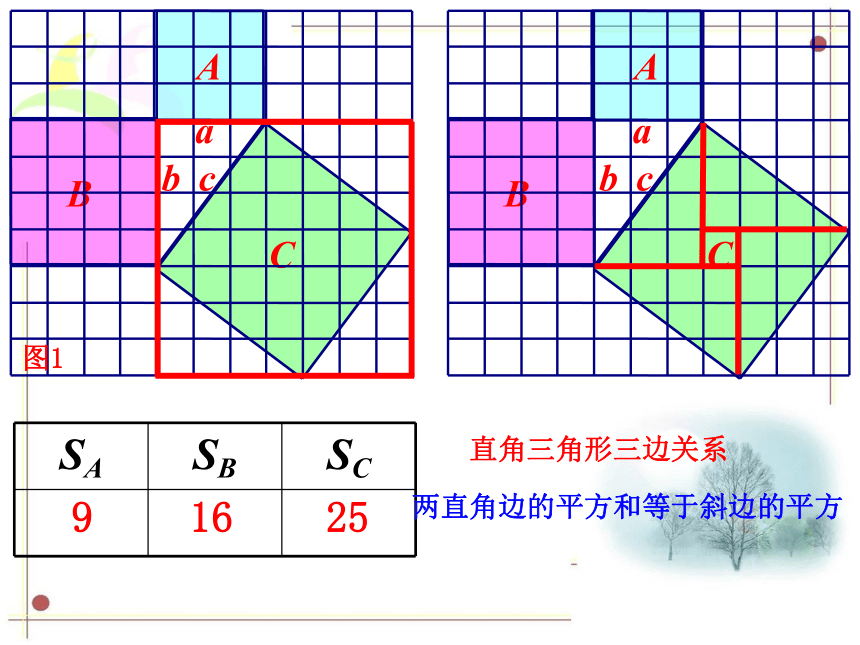
图中每个小方格的面积均为1,请分别算出正方形A,B,C 的面积,利用面积关系验证三边关系.
活动三
探究:一般直角三角形三边关系
A
B
SA SB SC
9
16
25
a
b
c
C
A
B
a
b
c
C
图1
直角三角形三边关系
两直角边的平方和等于斜边的平方
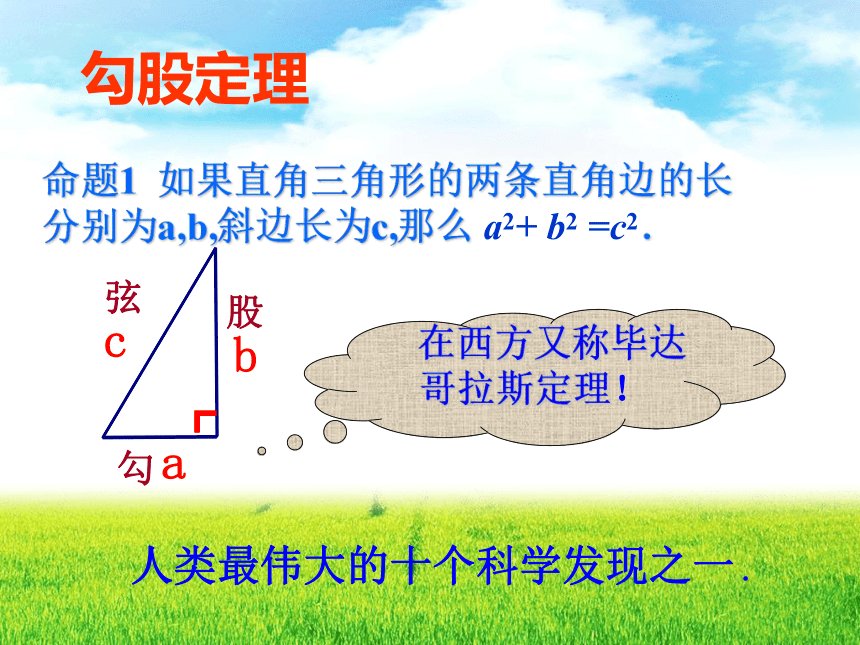
a
┏
c
b
勾
股
弦
人类最伟大的十个科学发现之一 .
勾股定理
在西方又称毕达哥拉斯定理!
命题1 如果直角三角形的两条直角边的长分别为a,b,斜边长为c,那么 a2+ b2 =c2.
赵爽弦图
c
a
b
c
a
b
c
a
b
c
a
b
该图2002年8月在北京召开的国际
数学家大会的会标,取材于我国古代
数学著作《勾股圆方图》。
证明1:
1、拿出准备好的四个全等的直角三角板,你能拼成一个中空的正方形吗?有几种拼法?
2、你能用你拼出的图形说明a2+b2=c2?
用图形面积不变和对图形面积不同的算法说明
(设直角边分别为a,b,斜边c)
c
a
b
画板拼图
证明结论
大正方形的面积可以表示为 ;
也可以表示为
c2
化简得: c2 =a2+ b2
a
b
a
c
c
c
c
a
a
b
b
b
思考:拼法一是用什么方法验证了c2 =a2+ b2?
拼法一
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
(a+b)2
=
a
c
c
c
c
a
a
b
a
b
b
b
拼法二
c
a
b
c
c
a
a
b
b
a
c
b
这就是有名的总统证法,他是用什么图形围成了一个直角梯形?梯形的面积怎样表示?
a2 + b2 = c2
化简得:
拼法三
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
勾股链接
勾
股
勾
股
弦
现有两个边长分别为a和b的正方形,通过分割、拼凑怎样拼成一个正方形?
b
a
观察与欣赏
赵爽弦图
a
b
a2 + b2
c2
c
这两个正方形还能怎样分割,拼成正方形?
=
青朱出入图
1.算一算:
17
8
x
12
x
5
(1)
(2)
基础练习
x=13
x=15
若直角三角形的两条边长为6cm,8cm,则第三边长一定为10cm.( )
×
小结:注意使用勾股定理和分类讨论的思想。
2.判断正误:
6
8
图一
6
8
图二
3.求下列图中字母所代表的正方形的面积:
①
81
144
②
144
169
A
B
225
25
美丽的勾股树
一种思想
数形结合
一份自豪
身为中国人
勾股定理
一个定理
特殊到一般
一次探索
收获
共享
颗粒归仓
我学到了什么知识;
我经历了怎样的过程;
我用到了哪些方法;
我用到哪些数学思想……
勾股定理
拼图法
面积法
割补法
方程
分类讨论
特殊一般
思想
方法
经历
发现
运用
验证
作业:
1.必做题:
课本习题17.1第1、2两题.
2.选做题:
试作一株美丽的勾股树。
其实数学在我们的生活中无处不在, 只要你是个有心人,就一定会发现在我们的身边,我们的眼前, 还有很多象 “勾股定理”那样的知识等待我们去探索,等待我们去发现……
教师寄语
17.1探究勾股定理
茫茫宇宙,浩瀚太空,如果有一天,我们真的和外星人相遇了,该用什么语言与他交流呢?曾经有科学家认为,用两个图形作为与外星人交谈的媒介,其中一个就是“数形关系”(勾股定理)。因为这种自然图形所具备的“数形关系”在整个宇宙中是普遍存在的。
学习目标
1.了解勾股定理的内容,并掌握直角三角形三边之间的数量关系。(重点)
2.能够运用勾股定理进行简单的计算。
(难点)
2500年前,古希腊著名数学家毕达哥拉斯非常善于观察和思考,经常能从平淡的生活现象中发现数学问题.
看一看
相传两千多年前,毕达哥拉斯去朋友家作客,发现朋友家的地面反映直角三角形三边的某种数量关系,我们快来观察下面的图案,看看你能发现什么?
⑴正方形A、B、C的面积是多少?面积之间有什么关系?
⑵直角三角形三边有什么关系?
SA+SB=SC
两直角边的平方和等于斜边的平方
探究:最简单的等腰直角三角形三边关系
活动一
A
B
C
(每个小正方形的边长为单位1)
a
c
b
A
B
C
A
B
C
(每个小正方形的边长为单位1)
图2-1
图2-2
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2-1
图2-2
A、B、C面积关系 直角三角形三边关系
探究:等腰直角三角形三边关系
活动二
9
9
18
4
4
两直角边的平方和
等于斜边的平方
SA+SB=SC
8
C
A
B
a
b
c
图中每个小方格的面积均为1,请分别算出正方形A,B,C 的面积,利用面积关系验证三边关系.
活动三
探究:一般直角三角形三边关系
A
B
SA SB SC
9
16
25
a
b
c
C
A
B
a
b
c
C
图1
直角三角形三边关系
两直角边的平方和等于斜边的平方
a
┏
c
b
勾
股
弦
人类最伟大的十个科学发现之一 .
勾股定理
在西方又称毕达哥拉斯定理!
命题1 如果直角三角形的两条直角边的长分别为a,b,斜边长为c,那么 a2+ b2 =c2.
赵爽弦图
c
a
b
c
a
b
c
a
b
c
a
b
该图2002年8月在北京召开的国际
数学家大会的会标,取材于我国古代
数学著作《勾股圆方图》。
证明1:
1、拿出准备好的四个全等的直角三角板,你能拼成一个中空的正方形吗?有几种拼法?
2、你能用你拼出的图形说明a2+b2=c2?
用图形面积不变和对图形面积不同的算法说明
(设直角边分别为a,b,斜边c)
c
a
b
画板拼图
证明结论
大正方形的面积可以表示为 ;
也可以表示为
c2
化简得: c2 =a2+ b2
a
b
a
c
c
c
c
a
a
b
b
b
思考:拼法一是用什么方法验证了c2 =a2+ b2?
拼法一
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
(a+b)2
=
a
c
c
c
c
a
a
b
a
b
b
b
拼法二
c
a
b
c
c
a
a
b
b
a
c
b
这就是有名的总统证法,他是用什么图形围成了一个直角梯形?梯形的面积怎样表示?
a2 + b2 = c2
化简得:
拼法三
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
勾股链接
勾
股
勾
股
弦
现有两个边长分别为a和b的正方形,通过分割、拼凑怎样拼成一个正方形?
b
a
观察与欣赏
赵爽弦图
a
b
a2 + b2
c2
c
这两个正方形还能怎样分割,拼成正方形?
=
青朱出入图
1.算一算:
17
8
x
12
x
5
(1)
(2)
基础练习
x=13
x=15
若直角三角形的两条边长为6cm,8cm,则第三边长一定为10cm.( )
×
小结:注意使用勾股定理和分类讨论的思想。
2.判断正误:
6
8
图一
6
8
图二
3.求下列图中字母所代表的正方形的面积:
①
81
144
②
144
169
A
B
225
25
美丽的勾股树
一种思想
数形结合
一份自豪
身为中国人
勾股定理
一个定理
特殊到一般
一次探索
收获
共享
颗粒归仓
我学到了什么知识;
我经历了怎样的过程;
我用到了哪些方法;
我用到哪些数学思想……
勾股定理
拼图法
面积法
割补法
方程
分类讨论
特殊一般
思想
方法
经历
发现
运用
验证
作业:
1.必做题:
课本习题17.1第1、2两题.
2.选做题:
试作一株美丽的勾股树。
其实数学在我们的生活中无处不在, 只要你是个有心人,就一定会发现在我们的身边,我们的眼前, 还有很多象 “勾股定理”那样的知识等待我们去探索,等待我们去发现……
教师寄语
