4.4 探索三角形相似的条件(第二课时) 课件(18张PPT)
文档属性
| 名称 | 4.4 探索三角形相似的条件(第二课时) 课件(18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-20 16:23:41 | ||
图片预览



文档简介
(共18张PPT)
4.4 探索三角形相似的条件
第四章 图形的相似
第二课时
学习目标
1)初步掌握“两边成比例且夹角相等的两个三角形相似”的判定方法.
2)经历两个三角形相似的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程;通过画图、度量等操作,培养学生获得数学猜想的经验,激发学生探索知识的兴趣,体验数学活动充满着探索性和创造性.
3)能够运用三角形相似的条件解决简单的问题.
重点
掌握判定方法,会运用判定方法判定两个三角形相似.
难点
能够运用三角形相似的条件解决简单的问题.
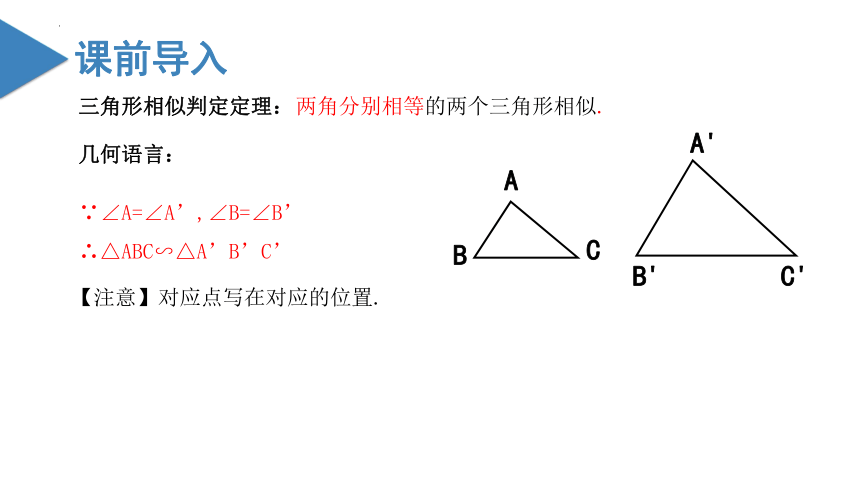
三角形相似判定定理:
几何语言:
∵∠A=∠A’,∠B=∠B’
∴△ABC∽△A’B’C’
两角分别相等的两个三角形相似.
【注意】对应点写在对应的位置.
A
C
B
C'
B'
A'
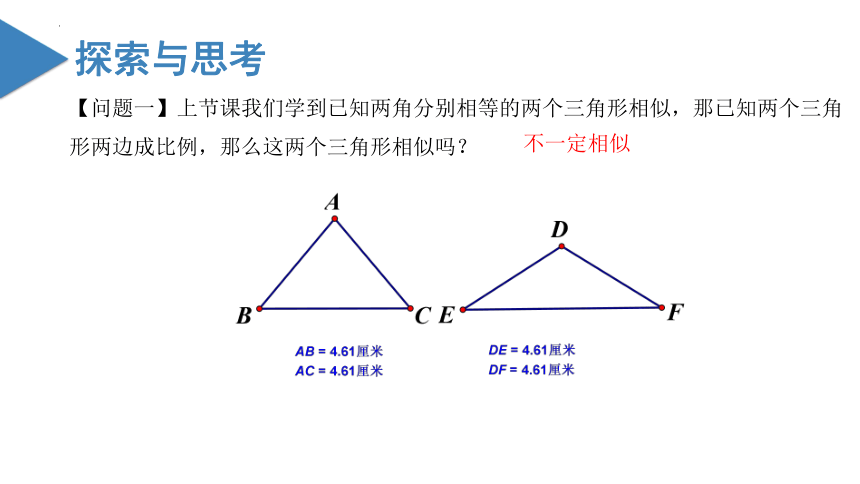
【问题一】上节课我们学到已知两角分别相等的两个三角形相似,那已知两个三角形两边成比例,那么这两个三角形相似吗?
不一定相似
【问题二】类比三角形全等的判定方法(SAS),已知两个三角形两边成比例,如果再增加一个条件,你能说出有哪几种可能出现的结果?
其中一边的对角
两边的夹角
增加一个角相等
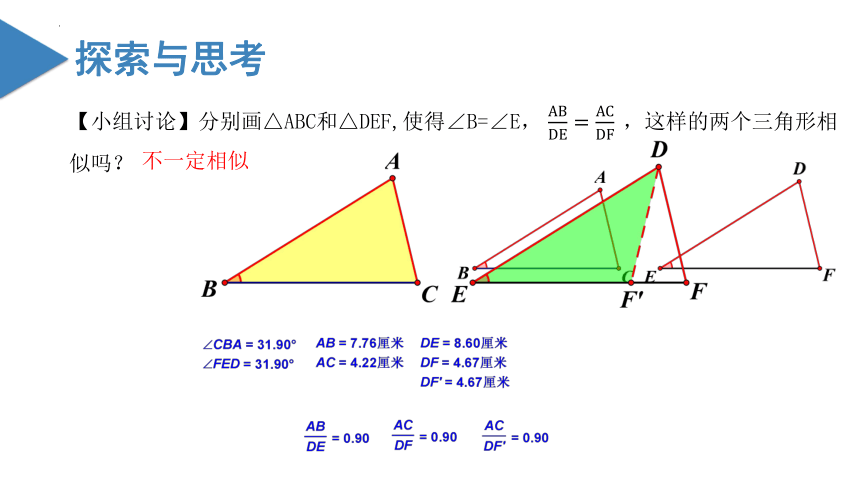
【小组讨论】分别画△ABC和△DEF,使得∠B=∠E, ,这样的两个三角形相似吗?
不一定相似
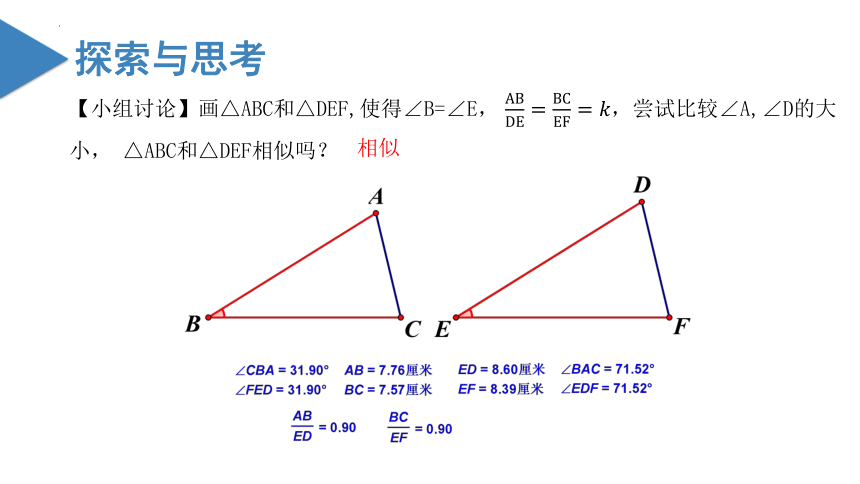
【小组讨论】画△ABC和△DEF,使得∠B=∠E, ,尝试比较∠A,∠D的大小, △ABC和△DEF相似吗?
相似
【问题三】改变k的大小,以上结论还成立吗?你发现了什么?
三角形相似判定定理2:
几何语言:
∵∠A=∠A’,
∴△ABC∽△A’B’C’
两边成比例且夹角相等的两个三角形相似.
A
C
B
C'
B'
A'
例1 如图,D,E分别是△ABC的边AC,AB上的点,AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
E
D
B
解:∵AE=1.5,AC=2,
∴ 而 ∴
又∵∠EAD=∠CAB,∴△ADE∽△ABC∴ =
∵ BC=3∴DE=BC= 3=
1. 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A. B. C. D.
【详解】∵∠BAC=∠D,,∴△ABC∽△ADE.故选C.
2. 如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )
A.AC:BC=AD:BD B.AC:BC=AB:AD
C.AB2=CD BC D.AB2=BD BC
【详解】∵∠B=∠B,∴当时,即AB2=BD BC时,△ABC∽△DBA,故选D.
3.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC C. D.
【详解】解:A.当∠ABP=∠C时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
B.当∠APB=∠ABC时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
C.当时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
D.无法得到△ABP∽△ACB,故此选项正确.故选:D.
4.如图,已知与,下列条件一定能推得它们相似的是( )
A. B.
C. D.
5.如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与相似的是( )
【详解】解:因为中有一个角是135°,而选项中有135°角的三角形只有B,且满足两边成比例夹角相等,故选B.
6.在和中,,,BC=4,,,判定这两个三角形是否相似 .(填“相似”或“不相似”)
7.如图,已知=,若使△ABC∽△ADE成立 (只添一种即可).
不相似
∠DAE=∠BAC
8.如图,在△ABC中,点D是AB上一点,且AD=1,AB=3,.
求证:△ACD∽△ABC.
证明:AD=1,AB=3,AC=
, 又
∽
9. 如图,AB AE=AD AC,且∠1=∠2,求证:△ABC∽△ADE.
证明:∵AB AE=AD AC,∴.
又∵∠1=∠2,∴∠2+∠BAE=∠1+∠BAE,
即∠BAC=∠DAE,
∴△ABC∽△AED.
4.4 探索三角形相似的条件
第四章 图形的相似
第二课时
学习目标
1)初步掌握“两边成比例且夹角相等的两个三角形相似”的判定方法.
2)经历两个三角形相似的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程;通过画图、度量等操作,培养学生获得数学猜想的经验,激发学生探索知识的兴趣,体验数学活动充满着探索性和创造性.
3)能够运用三角形相似的条件解决简单的问题.
重点
掌握判定方法,会运用判定方法判定两个三角形相似.
难点
能够运用三角形相似的条件解决简单的问题.
三角形相似判定定理:
几何语言:
∵∠A=∠A’,∠B=∠B’
∴△ABC∽△A’B’C’
两角分别相等的两个三角形相似.
【注意】对应点写在对应的位置.
A
C
B
C'
B'
A'
【问题一】上节课我们学到已知两角分别相等的两个三角形相似,那已知两个三角形两边成比例,那么这两个三角形相似吗?
不一定相似
【问题二】类比三角形全等的判定方法(SAS),已知两个三角形两边成比例,如果再增加一个条件,你能说出有哪几种可能出现的结果?
其中一边的对角
两边的夹角
增加一个角相等
【小组讨论】分别画△ABC和△DEF,使得∠B=∠E, ,这样的两个三角形相似吗?
不一定相似
【小组讨论】画△ABC和△DEF,使得∠B=∠E, ,尝试比较∠A,∠D的大小, △ABC和△DEF相似吗?
相似
【问题三】改变k的大小,以上结论还成立吗?你发现了什么?
三角形相似判定定理2:
几何语言:
∵∠A=∠A’,
∴△ABC∽△A’B’C’
两边成比例且夹角相等的两个三角形相似.
A
C
B
C'
B'
A'
例1 如图,D,E分别是△ABC的边AC,AB上的点,AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
E
D
B
解:∵AE=1.5,AC=2,
∴ 而 ∴
又∵∠EAD=∠CAB,∴△ADE∽△ABC∴ =
∵ BC=3∴DE=BC= 3=
1. 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A. B. C. D.
【详解】∵∠BAC=∠D,,∴△ABC∽△ADE.故选C.
2. 如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )
A.AC:BC=AD:BD B.AC:BC=AB:AD
C.AB2=CD BC D.AB2=BD BC
【详解】∵∠B=∠B,∴当时,即AB2=BD BC时,△ABC∽△DBA,故选D.
3.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC C. D.
【详解】解:A.当∠ABP=∠C时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
B.当∠APB=∠ABC时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
C.当时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
D.无法得到△ABP∽△ACB,故此选项正确.故选:D.
4.如图,已知与,下列条件一定能推得它们相似的是( )
A. B.
C. D.
5.如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与相似的是( )
【详解】解:因为中有一个角是135°,而选项中有135°角的三角形只有B,且满足两边成比例夹角相等,故选B.
6.在和中,,,BC=4,,,判定这两个三角形是否相似 .(填“相似”或“不相似”)
7.如图,已知=,若使△ABC∽△ADE成立 (只添一种即可).
不相似
∠DAE=∠BAC
8.如图,在△ABC中,点D是AB上一点,且AD=1,AB=3,.
求证:△ACD∽△ABC.
证明:AD=1,AB=3,AC=
, 又
∽
9. 如图,AB AE=AD AC,且∠1=∠2,求证:△ABC∽△ADE.
证明:∵AB AE=AD AC,∴.
又∵∠1=∠2,∴∠2+∠BAE=∠1+∠BAE,
即∠BAC=∠DAE,
∴△ABC∽△AED.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
