13.3.2等边三角形(第1课时) 课件(25张PPT)
文档属性
| 名称 | 13.3.2等边三角形(第1课时) 课件(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 746.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-20 15:55:31 | ||
图片预览




文档简介
(共25张PPT)
第13.3.2等边三角形
(第1课时)
人教版数学八年级上册
1.探索并掌握等边三角形性质的过程,并用以解决实际问题.
2.了解等边三角形的判定方法.
3.探索并掌握等边三角形判定的过程,并用以解决实际问题.
学习目标
1.等腰三角形有哪些特殊的性质呢?
从边的角度:两腰相等;
从角的角度:两个底角相等;
从对称性的角度:是轴对称图形、三线合一.
情境引入
思考:满足什么条件的三角形是等边三角形?
三条边都相等的三角形是等边三角形.
A
B
C
情境引入
探究1:如果把等腰三角形的性质用于等边三角形,你能得到什么结论?
结论:等边三角形的三条边都相等,是一种特殊的等腰三角形.所以等边三角形具有等腰三角形的所有性质.
互动新授
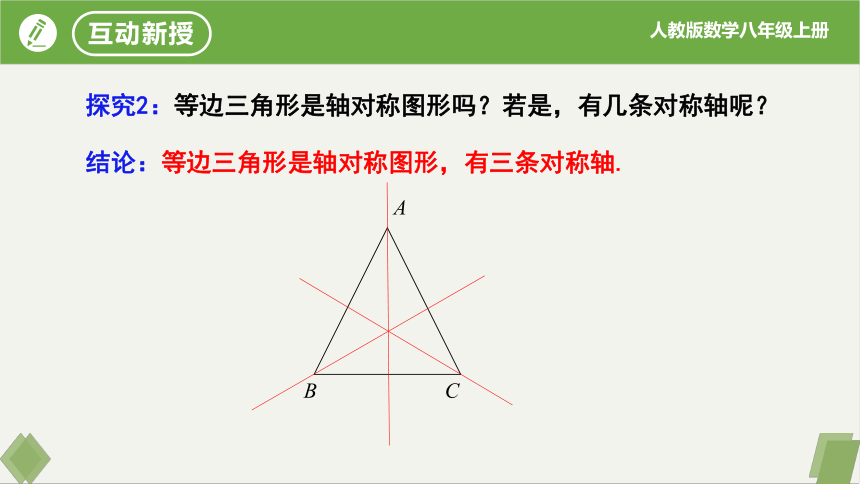
探究2:等边三角形是轴对称图形吗?若是,有几条对称轴呢?
结论:等边三角形是轴对称图形,有三条对称轴.
A
B
C
互动新授
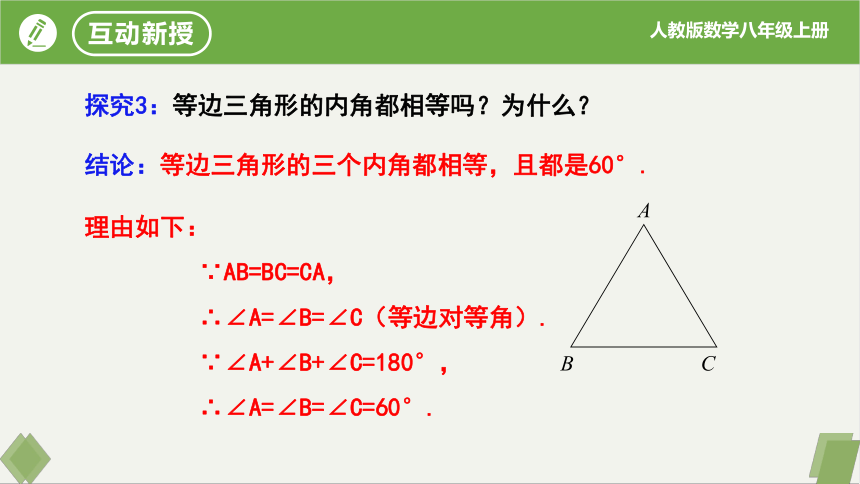
探究3:等边三角形的内角都相等吗?为什么?
结论:等边三角形的三个内角都相等,且都是60°.
理由如下:
∵AB=BC=CA,
∴∠A=∠B=∠C(等边对等角).
∵∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°.
A
B
C
互动新授
等边三角形的三个内角都相等,并且每一个角都等于60°.
符号语言表示:∵AB=BC=AC,
∴∠A=∠B=∠C=60°.
A
B
C
A
B
C
等边三角形的性质:
反之,三个角相等的三角形是等边三角形吗?
互动新授
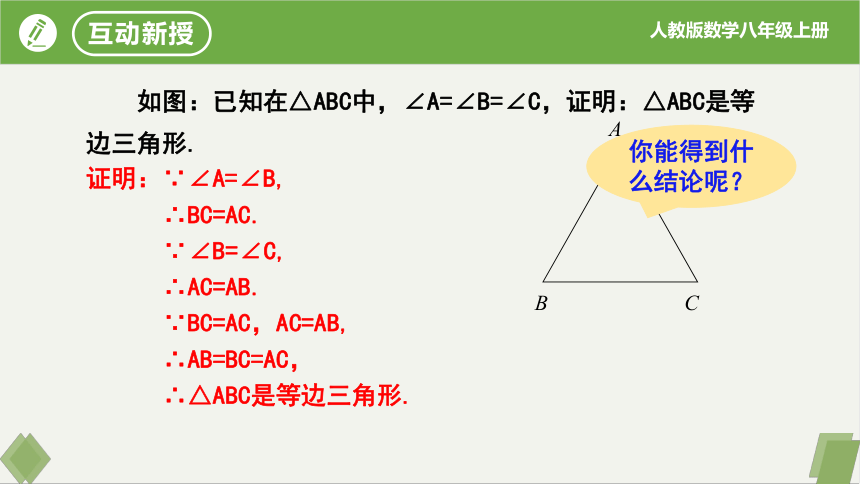
如图:已知在△ABC中,∠A=∠B=∠C,证明:△ABC是等边三角形.
证明:∵∠A=∠B,
∴BC=AC.
∵∠B=∠C,
∴AC=AB.
∵BC=AC,AC=AB,
∴AB=BC=AC,
∴△ABC是等边三角形.
A
B
C
你能得到什么结论呢?
互动新授
判定方法1:
三个角都相等的三角形是等边三角形.
符号语言表示: ∵∠A=∠B=∠C,
∴△ABC是等边三角形.
A
B
C
还有其他方法能判定三角形是等边三角形吗?
互动新授
探究4:等腰三角形有两边相等,能否添加什么条件使得等腰三角形成为等边三角形呢?
A
B
C
60°
有一个角是60°的等腰三角形
你能说明理由吗?
互动新授
如图:已知在△ABC中,AB=AC,∠A=60°.证明:△ABC是等边三角形.
证明:∵AB=AC,
∴∠C=∠B .
∵∠A=60°,
∴∠B+∠C=180°-∠A=120°,
∴∠A=∠B=∠C=60°.
∴△ABC是等边三角形.
A
B
C
60°
如果60°的角不是顶角,而是底角呢?
互动新授
证明:∵AB=AC,∠B=60° ,
∴∠C=∠B=60° .
∴∠A=180°-(∠B+∠C)=60° ,
∴∠A=∠B=∠C.
∴△ABC是等边三角形.
如图:已知在△ABC中,AB=AC,∠B=60°,证明:△ABC是等边三角形.
A
B
C
60°
互动新授
判定方法2:
有一个角是60°的等腰三角形是等边三角形.
A
B
C
60°
符号语言表示: ∵AB=AC,∠B=60°,
∴△ABC是等边三角形.
在等腰三角形中,只要有一个角是60°,无论这个角是顶角还是底角,这个三角形就是等边三角形.
注意:
互动新授
例4 如图,△ABC是等边三角形,DE//BC,分别交AB,AC于点D,E.求证:△ADE是等边三角形.
证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C.
∵DE//BC,
∴∠ADE=∠B,∠AED=∠C.
∴∠A=∠ADE=∠AED.
∴△ADE是等边三角形.
A
B
C
D
E
典例精析
1.下面给出的几种三角形:
A.4个 B.3个 C.2个 D.1个
①有两个角是60°的三角形;
②三个外角都相等的三角形;
③一边上的高也是这边上的中线的三角形;
④有一个外角120°的等腰三角形
其中一定是等边三角形的有( )
B
小试牛刀
2.下列推理中,错误的是( )
A.因为∠A=∠B=∠C,所以△ABC是等边三角形
B.因为AB=AC且∠B=∠C,所以△ABC是等边三角形
C.因为∠A=60°,∠B=60°,所以△ABC是等边三角形
D.因为AB=AC,∠B=60°,所以△ABC是等边三角形
B
小试牛刀
课堂检测
1.如图,△ABC是等边三角形,点D在AC边上,∠DBC=35°,则∠ADB的度数为( )
A.25° B.60°
C.85° D.95°
2.如图,△ABC为等边三角形,AD⊥BC,AE=AD则∠ADE的度数为( )
A.30° B.60°
C.45 D.75°
D
D
3.如图,△ABC的边BC上有D、E两点,且BD=DE=EC=AD=AE,则∠BAC=_____.
120°
4.如图,在△ABC中,∠BAC=120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC的长为( )
A.9 B.8 C.6 D.7
B
第3题图 第4题图
课堂检测
解:∵DE⊥AC,
∴∠DFA=∠EFA=90°.
∵AD=AE,∠DAE=80°,
∴∠ADE=∠E=50°.
∴∠DAF=∠EAF=40°.
∵△ABC是等边三角形,
∴∠BAC=60°.
∴∠BAD=∠BAC-∠DAF=20°.
∵∠B+∠BAD=∠ADC=∠ADE+∠EDC,
∴∠EDC=60°+20°-50°=30°.
1.如图,△ABC是等边三角形,△ADE是等腰三角形,AD=AE,∠DAE=80°,当DE⊥AC时,求∠BAD和∠EDC的度数.
A
B
C
F
E
D
拓展训练
拓展训练
2.如图,△ABC是等边三角形,∠ABC、∠ACB的平分线交于点O,OM∥AB,ON∥AC.求证:BM=MN=CN.
证明:∵△ABC是等边三角形
∴∠ABC=60°
∵OB平分∠ABC
∴∠1=∠2=30°
∵OM//AB
∴∠1=∠3
∴∠2=∠3=30°
∴BM=OM,∠OMN=60°同理CN=ON,∠ONM=60°
∴∠OMN=∠ONM=∠MON=60°
∴OM=ON=MN
∴BM=MN=CN
等边三角形的判定
性质
判定方法2
三边相等的三角形是
等边三角形.
有一个角是60°的等腰三角形是等边三角形.
判定方法1
三个角都相等的三角形是
等边三角形.
课堂小结
1.如图,已知△ABC是等边三角形,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=( )
A.15° B.20° C.25° D.30°
解:∵△ABC是等边三角形,
∴∠ACB=60°.
∵CG=CD,
∴∠CGD =∠CDG.
∴∠ACB =∠CGD+∠CDG=2∠CDG.
同理可得∠CDG=2∠E,
∴∠ACB =4∠E=60°.
∴∠E=15°.
A
课后作业
课后作业
2.如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.求证:BD=DE.
证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°,∠DBC=30°.
∵CE=CD,
∴∠CDE=∠CED.
∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边).
谢谢聆听
第13.3.2等边三角形
(第1课时)
人教版数学八年级上册
1.探索并掌握等边三角形性质的过程,并用以解决实际问题.
2.了解等边三角形的判定方法.
3.探索并掌握等边三角形判定的过程,并用以解决实际问题.
学习目标
1.等腰三角形有哪些特殊的性质呢?
从边的角度:两腰相等;
从角的角度:两个底角相等;
从对称性的角度:是轴对称图形、三线合一.
情境引入
思考:满足什么条件的三角形是等边三角形?
三条边都相等的三角形是等边三角形.
A
B
C
情境引入
探究1:如果把等腰三角形的性质用于等边三角形,你能得到什么结论?
结论:等边三角形的三条边都相等,是一种特殊的等腰三角形.所以等边三角形具有等腰三角形的所有性质.
互动新授
探究2:等边三角形是轴对称图形吗?若是,有几条对称轴呢?
结论:等边三角形是轴对称图形,有三条对称轴.
A
B
C
互动新授
探究3:等边三角形的内角都相等吗?为什么?
结论:等边三角形的三个内角都相等,且都是60°.
理由如下:
∵AB=BC=CA,
∴∠A=∠B=∠C(等边对等角).
∵∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°.
A
B
C
互动新授
等边三角形的三个内角都相等,并且每一个角都等于60°.
符号语言表示:∵AB=BC=AC,
∴∠A=∠B=∠C=60°.
A
B
C
A
B
C
等边三角形的性质:
反之,三个角相等的三角形是等边三角形吗?
互动新授
如图:已知在△ABC中,∠A=∠B=∠C,证明:△ABC是等边三角形.
证明:∵∠A=∠B,
∴BC=AC.
∵∠B=∠C,
∴AC=AB.
∵BC=AC,AC=AB,
∴AB=BC=AC,
∴△ABC是等边三角形.
A
B
C
你能得到什么结论呢?
互动新授
判定方法1:
三个角都相等的三角形是等边三角形.
符号语言表示: ∵∠A=∠B=∠C,
∴△ABC是等边三角形.
A
B
C
还有其他方法能判定三角形是等边三角形吗?
互动新授
探究4:等腰三角形有两边相等,能否添加什么条件使得等腰三角形成为等边三角形呢?
A
B
C
60°
有一个角是60°的等腰三角形
你能说明理由吗?
互动新授
如图:已知在△ABC中,AB=AC,∠A=60°.证明:△ABC是等边三角形.
证明:∵AB=AC,
∴∠C=∠B .
∵∠A=60°,
∴∠B+∠C=180°-∠A=120°,
∴∠A=∠B=∠C=60°.
∴△ABC是等边三角形.
A
B
C
60°
如果60°的角不是顶角,而是底角呢?
互动新授
证明:∵AB=AC,∠B=60° ,
∴∠C=∠B=60° .
∴∠A=180°-(∠B+∠C)=60° ,
∴∠A=∠B=∠C.
∴△ABC是等边三角形.
如图:已知在△ABC中,AB=AC,∠B=60°,证明:△ABC是等边三角形.
A
B
C
60°
互动新授
判定方法2:
有一个角是60°的等腰三角形是等边三角形.
A
B
C
60°
符号语言表示: ∵AB=AC,∠B=60°,
∴△ABC是等边三角形.
在等腰三角形中,只要有一个角是60°,无论这个角是顶角还是底角,这个三角形就是等边三角形.
注意:
互动新授
例4 如图,△ABC是等边三角形,DE//BC,分别交AB,AC于点D,E.求证:△ADE是等边三角形.
证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C.
∵DE//BC,
∴∠ADE=∠B,∠AED=∠C.
∴∠A=∠ADE=∠AED.
∴△ADE是等边三角形.
A
B
C
D
E
典例精析
1.下面给出的几种三角形:
A.4个 B.3个 C.2个 D.1个
①有两个角是60°的三角形;
②三个外角都相等的三角形;
③一边上的高也是这边上的中线的三角形;
④有一个外角120°的等腰三角形
其中一定是等边三角形的有( )
B
小试牛刀
2.下列推理中,错误的是( )
A.因为∠A=∠B=∠C,所以△ABC是等边三角形
B.因为AB=AC且∠B=∠C,所以△ABC是等边三角形
C.因为∠A=60°,∠B=60°,所以△ABC是等边三角形
D.因为AB=AC,∠B=60°,所以△ABC是等边三角形
B
小试牛刀
课堂检测
1.如图,△ABC是等边三角形,点D在AC边上,∠DBC=35°,则∠ADB的度数为( )
A.25° B.60°
C.85° D.95°
2.如图,△ABC为等边三角形,AD⊥BC,AE=AD则∠ADE的度数为( )
A.30° B.60°
C.45 D.75°
D
D
3.如图,△ABC的边BC上有D、E两点,且BD=DE=EC=AD=AE,则∠BAC=_____.
120°
4.如图,在△ABC中,∠BAC=120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC的长为( )
A.9 B.8 C.6 D.7
B
第3题图 第4题图
课堂检测
解:∵DE⊥AC,
∴∠DFA=∠EFA=90°.
∵AD=AE,∠DAE=80°,
∴∠ADE=∠E=50°.
∴∠DAF=∠EAF=40°.
∵△ABC是等边三角形,
∴∠BAC=60°.
∴∠BAD=∠BAC-∠DAF=20°.
∵∠B+∠BAD=∠ADC=∠ADE+∠EDC,
∴∠EDC=60°+20°-50°=30°.
1.如图,△ABC是等边三角形,△ADE是等腰三角形,AD=AE,∠DAE=80°,当DE⊥AC时,求∠BAD和∠EDC的度数.
A
B
C
F
E
D
拓展训练
拓展训练
2.如图,△ABC是等边三角形,∠ABC、∠ACB的平分线交于点O,OM∥AB,ON∥AC.求证:BM=MN=CN.
证明:∵△ABC是等边三角形
∴∠ABC=60°
∵OB平分∠ABC
∴∠1=∠2=30°
∵OM//AB
∴∠1=∠3
∴∠2=∠3=30°
∴BM=OM,∠OMN=60°同理CN=ON,∠ONM=60°
∴∠OMN=∠ONM=∠MON=60°
∴OM=ON=MN
∴BM=MN=CN
等边三角形的判定
性质
判定方法2
三边相等的三角形是
等边三角形.
有一个角是60°的等腰三角形是等边三角形.
判定方法1
三个角都相等的三角形是
等边三角形.
课堂小结
1.如图,已知△ABC是等边三角形,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=( )
A.15° B.20° C.25° D.30°
解:∵△ABC是等边三角形,
∴∠ACB=60°.
∵CG=CD,
∴∠CGD =∠CDG.
∴∠ACB =∠CGD+∠CDG=2∠CDG.
同理可得∠CDG=2∠E,
∴∠ACB =4∠E=60°.
∴∠E=15°.
A
课后作业
课后作业
2.如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.求证:BD=DE.
证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°,∠DBC=30°.
∵CE=CD,
∴∠CDE=∠CED.
∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边).
谢谢聆听
