25.4 解直角三角形的应用 课件(41张PPT)
文档属性
| 名称 | 25.4 解直角三角形的应用 课件(41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 40.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-20 16:01:29 | ||
图片预览








文档简介
(共41张PPT)
25.4解直角三角形的应用
第25章 锐角的三角比
教师
xxx
沪教版 九年级第一学期
与方位角有关的问题
利用坡度和坡角解决问题
仰角和俯角问题
01
03
02
CONTANTS
目 录
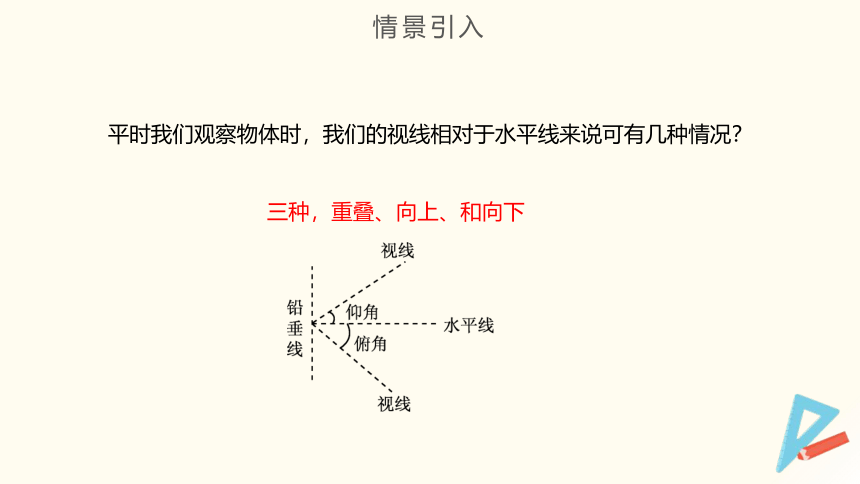
平时我们观察物体时,我们的视线相对于水平线来说可有几种情况?
三种,重叠、向上、和向下
情景引入
与方位角有关的问题
01
与方位角有关的实际问题
方向角:
如图,指北或指南的方向线与目标方向线所成的小于90°的角叫做方向角.
30°
45°
B
O
A
东
西
北
南
探究新知
东
北
A
B
C
25°
例1:如图,海中有一个小岛A,该岛四周10海里内有暗礁.
一货轮由西向东航行,开始在A岛南偏西55 的B处,往东行驶20海里后到达该岛的南偏西25 的C处.之后,货轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?
55°
探究新知
A
B
55°
C
25°
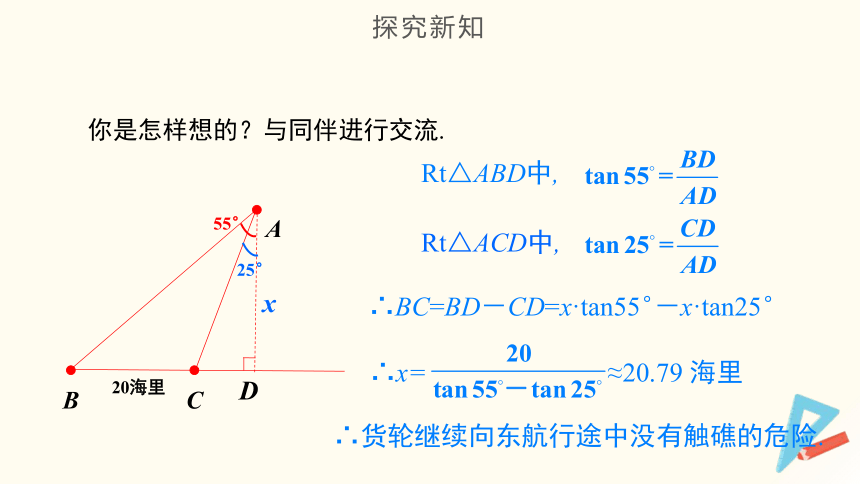
你是怎样想的?与同伴进行交流.
20海里
D
x
Rt△ABD中,
Rt△ACD中,
∴BC=BD-CD=x·tan55°-x·tan25°
∴x= ≈20.79 海里
∴货轮继续向东航行途中没有触礁的危险.
探究新知
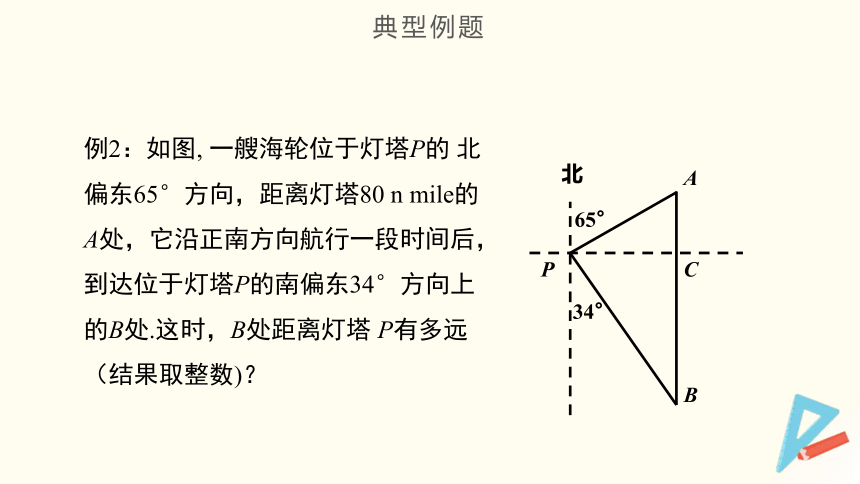
例2:如图, 一艘海轮位于灯塔P的 北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处.这时,B处距离灯塔 P有多远(结果取整数)?
A
P
C
B
北
65°
34°
典型例题
A
P
C
B
北
65°
34°
解:如图,在Rt△APC中,
PC =PA cos(90°-65°)
=80 × cos 25°
≈72. 505.
在 Rt△BPC 中, ∠B = 34°,
因此,当海轮到达位于灯塔P的南偏东34°方向
时,它距离灯塔P大约 130 n mile.
典型例题
归纳总结
利用解直角三角形解决简单问题的一般解题步骤:
1. 将实际问题抽象为数学问题;
2. 根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3. 得到数学问题的答案;
4. 得到实际问题的答案.
探究新知
仰角和俯角问题
02
仰角和俯角问题
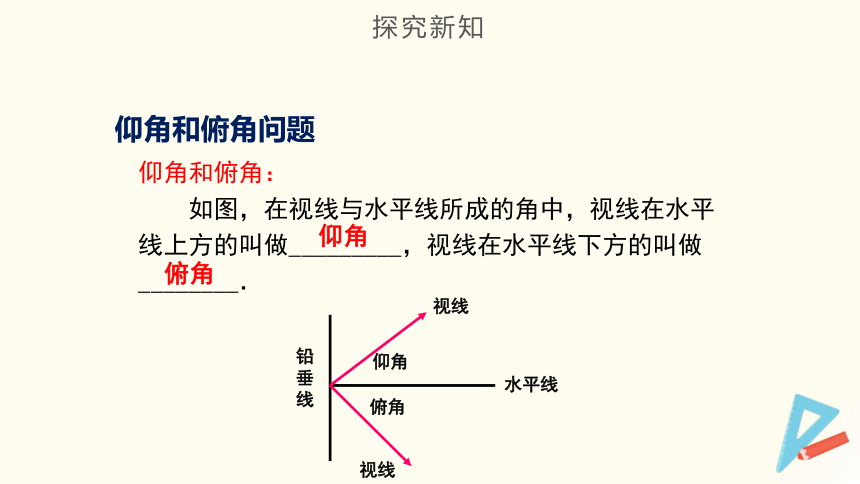
仰角和俯角:
如图,在视线与水平线所成的角中,视线在水平线上方的叫做_________,视线在水平线下方的叫做________.
仰角
俯角
视线
铅垂线
水平线
视线
仰角
俯角
探究新知
例3 如图,某班学生利用周末到白塔山去参观“晏阳初博物馆”.下面是两位同学的一段对话:
甲:我站在N 处看塔顶,仰角为60°.
乙:我站在M 处看塔顶,仰角为30°.
甲:我们的身高都是1.5 m.
乙:我们和塔在一条直线上,且我们相距20 m.请你根据两位同学的对话,计算白塔的高度.(结果精确到1 m).
典型例题
由题意知∠CAB=30°,∠CBD=60°,AB=20 m,
AM=BN=DP=1.5 m.
在△ABC中,∠CBD=∠ACB+∠CAB,
∴∠ACB=60°-30°=30°.
∴∠ACB=∠CAB. ∴BC=AB=20 m.
在Rt△CBD 中,BC=20 m,∠CBD=60°,
sin ∠CBD=
∴CD=BC·sin ∠CBD=20sin 60°=20× (m).
∴CP=CD+DP=10 +1.5≈19(m).
答:白塔的高度约为19 m.
解:
典型例题
例4 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.Rt△ABD中,
α=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
A
B
C
D
α
β
仰角
水平线
俯角
典型例题
解:如图,α = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
A
B
C
D
α
β
典型例题
总 结
从不同位置看同一点测高度时,往往用高度来表示这两个不同位置到被测物底部的距离.然后利用两次测量的不同位置之间的距离来解决问题.
探究新知
如图,某飞机在空中A 处探测到它的正 下方地平面上目标C,此时飞行高度AC=1 200 m,从飞机上看地平面指挥台B 的俯角α=30°,则飞机A与指挥台B 的距离为( )
A.1 200 m
B.1 200 m
C.1 200 m
D.2 400 m
D
针对练习
2 如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30 m的B 处,测得树顶A 的仰角∠ABO 为α,则树OA的高度为( )
A. m
B.30sin α m
C.30tan α m
D.30cos α m
C
针对练习
3 湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB 底部50 m的C 处,测得桥塔顶部A的仰角为41.5°(如图).已知测量仪器CD 的高度为1 m,则桥塔AB 的高度约为( )(参考数据:sin 41.5°≈0.663,
cos 41.5°≈0.749,
tan 41.5°≈0.885)
A.34 m B.38 m
C.45 m D.50 m
C
针对练习
利用坡度和坡角解决问题
03
利用坡角解决实际问题
坡度和坡角:
如图,通常把坡面的铅直高度h和水平宽度l之比叫_______,用字母i表示,把坡面与水平面的夹角叫做_______,记做α,于是i=____=tanα,显然,坡度越大,α角越大,坡面就越陡.
坡角
坡度
l
h
α
α为坡角
坡度和坡角有什么区别?
探究新知
例5 一个长方体木箱沿斜面下滑,当木箱滑至如图所示的位置时,AB=3 m,已知木箱高BE= m,斜面坡角为30°,求木箱端点E距地面AC的高度EF.
连接AE,在Rt△ABE 中求出AE,且根据∠EAB 的正
切值求出∠EAB 的度数,
进而得到∠EAF 的度数,
最后在Rt△EAF 中解出
EF 即可.
导引:
典型例题
连接AE,如图所示.
在Rt△ABE中,AB=3,BE=
则AE=
∵tan ∠EAB=
∴∠EAB=30°.
在Rt△AEF中,
∠EAF=∠EAB+∠BAC=30°+30°=60°,
∴EF=AE×sin ∠EAF=
答:木箱端点E距地面AC的高度EF为3 m.
解:
典型例题
如图,将一个Rt△ABC 形状的楔子从木桩的底端点P沿水平方向打入木桩底下,使木桩向上运动.已知楔子斜面的倾斜角为15°,若楔子沿水平方向前进6 cm(如箭头所示),则木桩上升了( )
A.6sin 15° cm B.6cos 15° cm
C.6tan 15° cm D. cm
C
针对练习
如图,长4 m的楼梯AB 的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD 为45°,则调整后的楼梯AC 的长为( )
A. m
B. m
C.(2 -2)m
D.(2 -2)m
B
针对练习
例6 小明沿着坡比为1∶2的山坡向上走了1 000 m,则
他升高了( )
A.200 m B.500 m
C.500 m D.1 000 m
如图,设他升高了h m,
∵i= BC=h m,
∴AC=2h m.由BC 2+AC 2=AB 2,
得h 2+(2h)2=1 0002,
∴h 2=2×105,即h=200
A
导引:
坡比的应用
典型例题
如图,斜面AC 的坡度(CD 与AD 的比)为1:2,AC=3 米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC 的高度为( )
A.5米
B.6米
C.8米
D.(3+ )米
A
针对练习
如图,某办公大楼正前方有一根高度是15 m的旗杆ED,从办公楼顶端A测得旗杆顶端E 的俯角α 是45°,旗杆底端D到大楼前梯坎底边的距离DC 是20 m,梯坎坡长BC 是12 m,梯坎坡度i=
1∶ ,则大楼AB 的高度约为(精确到0.1米,参
考数据: ≈1.41, ≈1.73, ≈2.45)( )
A.30.6 m
B.32.1 m
C.37.9 m
D.39.4 m
D
针对练习
1.从一艘船上测得海岸_上高为42米的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )
A.42米 B.14米 C.21米 D.42米.
2.身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
A.甲 B.乙 C.丙 D.丁
A
D
课堂练习
3.如图,某航天飞船在地球表面点P的正上方A处,从A处观测到地球表面的最远点Q,若∠QAP=a,地球半径为R,则航天飞船距离地球表面的最近距离AP以及P,Q两点间的地面距离分别是( )
A. B.
C. D.
B
课堂练习
4.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BC0=x,则点A到OC的距离等于( )
A. a·sinx+b·sinx
B. a·cosx+b·cosx
C. a·sinx+b·cosx
D. a·cosx+b·sinx
D
课堂练习
5.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为
_________m.(结果保留根号)
6.如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影子约为10米,则大树的高约为______米. (结果保留根号)
5+5
1
课堂练习
7.某公共场所准备改善原有楼梯的安全性能,把倾角由45°减至30°,楼梯高度不变.已知楼梯原长4m,那么调整的楼梯.会增加多长 楼梯多占了多长一段地面
解:在Rt△ABC中,AB=4,∠ABC=45°
∴BC=AC=AB·sin45°=2m
在Rt△ADC中,AC=2,∠ADC=30°
∴AD= m,DC= m
∴AD-AB=(4-4)m,DC-BC=(2-2)m
答:调整后楼梯会增加(4-4)m,占地会加长(2-2)m.
课堂练习
8.如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m)
解:在Rt△ACD中,∠A=30°
∴tan30 °= ∴AC=CD
在Rt△BCD中,∠CBD=60°
∴tan60°= ,∴BC=CD
∵AC-BC=50,∴CD-CD=50 解得,CD≈43
答:该塔约为43m高.
课堂练习
9.为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE=10m,其坡度为i1=1:,将步梯DE改造为斜坡AF,其坡度为i2=1:4,求斜坡AF的长度(结果精确到0.01m,参考数据: ≈1.732, ≈4.123).
课堂练习
解:∵DE=10m,其坡度为i1=1:
∴CE=CD
由勾股定理得 ,解得CD=5m
∵四边形ABCD为矩形,∴AB=CD=5m
∵斜坡AF的坡度为i2=1:4
∴
∴BF=4AB=20m
在Rt△ABF中,
故斜坡AF的长度约为20.62m.
课堂练习
10.八仙阁是八仙山公园里的一个主景区,八仙阁也是晋江的一个标志性建筑.在阁楼上可以看到整个八仙山公园全景,甚至周围景观都能尽收眼底.小明想知道它的高度.于是走到点C处,测得此时塔尖A的仰角是37,向前走了15.5米至点F处,测得此时塔尖A的仰角是,已知小明的眼睛离地面高度是1.5米,请聪明的你帮他求出八仙阁AB的高度.(参考数据:,,)
课堂练习
9.八仙阁是八仙山公园里的一个主景区,八仙阁也是晋江的一个标志性建筑.在阁楼上可以看到整个八仙山公园全景,甚至周围景观都能尽收眼底.小明想知道它的高度.于是走到点C处,测得此时塔尖A的仰角是37,向前走了15.5米至点F处,测得此时塔尖A的仰角是,已知小明的眼睛离地面高度是1.5米,请聪明的你帮他求出八仙阁AB的高度.(参考数据:,,)
解:由题意得,,
则四边形均为矩形.
所以米,米,
在中,,则.设米,
课堂练习
9.八仙阁是八仙山公园里的一个主景区,八仙阁也是晋江的一个标志性建筑.在阁楼上可以看到整个八仙山公园全景,甚至周围景观都能尽收眼底.小明想知道它的高度.于是走到点C处,测得此时塔尖A的仰角是37,向前走了15.5米至点F处,测得此时塔尖A的仰角是,已知小明的眼睛离地面高度是1.5米,请聪明的你帮他求出八仙阁AB的高度.(参考数据:,,)
在中,,
则,即,
解得:,
所以米,
则(米).
答:八仙阁AB的高度为48米.
课堂练习
感谢观看
25.4解直角三角形的应用
第25章 锐角的三角比
教师
xxx
沪教版 九年级第一学期
与方位角有关的问题
利用坡度和坡角解决问题
仰角和俯角问题
01
03
02
CONTANTS
目 录
平时我们观察物体时,我们的视线相对于水平线来说可有几种情况?
三种,重叠、向上、和向下
情景引入
与方位角有关的问题
01
与方位角有关的实际问题
方向角:
如图,指北或指南的方向线与目标方向线所成的小于90°的角叫做方向角.
30°
45°
B
O
A
东
西
北
南
探究新知
东
北
A
B
C
25°
例1:如图,海中有一个小岛A,该岛四周10海里内有暗礁.
一货轮由西向东航行,开始在A岛南偏西55 的B处,往东行驶20海里后到达该岛的南偏西25 的C处.之后,货轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?
55°
探究新知
A
B
55°
C
25°
你是怎样想的?与同伴进行交流.
20海里
D
x
Rt△ABD中,
Rt△ACD中,
∴BC=BD-CD=x·tan55°-x·tan25°
∴x= ≈20.79 海里
∴货轮继续向东航行途中没有触礁的危险.
探究新知
例2:如图, 一艘海轮位于灯塔P的 北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处.这时,B处距离灯塔 P有多远(结果取整数)?
A
P
C
B
北
65°
34°
典型例题
A
P
C
B
北
65°
34°
解:如图,在Rt△APC中,
PC =PA cos(90°-65°)
=80 × cos 25°
≈72. 505.
在 Rt△BPC 中, ∠B = 34°,
因此,当海轮到达位于灯塔P的南偏东34°方向
时,它距离灯塔P大约 130 n mile.
典型例题
归纳总结
利用解直角三角形解决简单问题的一般解题步骤:
1. 将实际问题抽象为数学问题;
2. 根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3. 得到数学问题的答案;
4. 得到实际问题的答案.
探究新知
仰角和俯角问题
02
仰角和俯角问题
仰角和俯角:
如图,在视线与水平线所成的角中,视线在水平线上方的叫做_________,视线在水平线下方的叫做________.
仰角
俯角
视线
铅垂线
水平线
视线
仰角
俯角
探究新知
例3 如图,某班学生利用周末到白塔山去参观“晏阳初博物馆”.下面是两位同学的一段对话:
甲:我站在N 处看塔顶,仰角为60°.
乙:我站在M 处看塔顶,仰角为30°.
甲:我们的身高都是1.5 m.
乙:我们和塔在一条直线上,且我们相距20 m.请你根据两位同学的对话,计算白塔的高度.(结果精确到1 m).
典型例题
由题意知∠CAB=30°,∠CBD=60°,AB=20 m,
AM=BN=DP=1.5 m.
在△ABC中,∠CBD=∠ACB+∠CAB,
∴∠ACB=60°-30°=30°.
∴∠ACB=∠CAB. ∴BC=AB=20 m.
在Rt△CBD 中,BC=20 m,∠CBD=60°,
sin ∠CBD=
∴CD=BC·sin ∠CBD=20sin 60°=20× (m).
∴CP=CD+DP=10 +1.5≈19(m).
答:白塔的高度约为19 m.
解:
典型例题
例4 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.Rt△ABD中,
α=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
A
B
C
D
α
β
仰角
水平线
俯角
典型例题
解:如图,α = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
A
B
C
D
α
β
典型例题
总 结
从不同位置看同一点测高度时,往往用高度来表示这两个不同位置到被测物底部的距离.然后利用两次测量的不同位置之间的距离来解决问题.
探究新知
如图,某飞机在空中A 处探测到它的正 下方地平面上目标C,此时飞行高度AC=1 200 m,从飞机上看地平面指挥台B 的俯角α=30°,则飞机A与指挥台B 的距离为( )
A.1 200 m
B.1 200 m
C.1 200 m
D.2 400 m
D
针对练习
2 如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30 m的B 处,测得树顶A 的仰角∠ABO 为α,则树OA的高度为( )
A. m
B.30sin α m
C.30tan α m
D.30cos α m
C
针对练习
3 湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB 底部50 m的C 处,测得桥塔顶部A的仰角为41.5°(如图).已知测量仪器CD 的高度为1 m,则桥塔AB 的高度约为( )(参考数据:sin 41.5°≈0.663,
cos 41.5°≈0.749,
tan 41.5°≈0.885)
A.34 m B.38 m
C.45 m D.50 m
C
针对练习
利用坡度和坡角解决问题
03
利用坡角解决实际问题
坡度和坡角:
如图,通常把坡面的铅直高度h和水平宽度l之比叫_______,用字母i表示,把坡面与水平面的夹角叫做_______,记做α,于是i=____=tanα,显然,坡度越大,α角越大,坡面就越陡.
坡角
坡度
l
h
α
α为坡角
坡度和坡角有什么区别?
探究新知
例5 一个长方体木箱沿斜面下滑,当木箱滑至如图所示的位置时,AB=3 m,已知木箱高BE= m,斜面坡角为30°,求木箱端点E距地面AC的高度EF.
连接AE,在Rt△ABE 中求出AE,且根据∠EAB 的正
切值求出∠EAB 的度数,
进而得到∠EAF 的度数,
最后在Rt△EAF 中解出
EF 即可.
导引:
典型例题
连接AE,如图所示.
在Rt△ABE中,AB=3,BE=
则AE=
∵tan ∠EAB=
∴∠EAB=30°.
在Rt△AEF中,
∠EAF=∠EAB+∠BAC=30°+30°=60°,
∴EF=AE×sin ∠EAF=
答:木箱端点E距地面AC的高度EF为3 m.
解:
典型例题
如图,将一个Rt△ABC 形状的楔子从木桩的底端点P沿水平方向打入木桩底下,使木桩向上运动.已知楔子斜面的倾斜角为15°,若楔子沿水平方向前进6 cm(如箭头所示),则木桩上升了( )
A.6sin 15° cm B.6cos 15° cm
C.6tan 15° cm D. cm
C
针对练习
如图,长4 m的楼梯AB 的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD 为45°,则调整后的楼梯AC 的长为( )
A. m
B. m
C.(2 -2)m
D.(2 -2)m
B
针对练习
例6 小明沿着坡比为1∶2的山坡向上走了1 000 m,则
他升高了( )
A.200 m B.500 m
C.500 m D.1 000 m
如图,设他升高了h m,
∵i= BC=h m,
∴AC=2h m.由BC 2+AC 2=AB 2,
得h 2+(2h)2=1 0002,
∴h 2=2×105,即h=200
A
导引:
坡比的应用
典型例题
如图,斜面AC 的坡度(CD 与AD 的比)为1:2,AC=3 米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC 的高度为( )
A.5米
B.6米
C.8米
D.(3+ )米
A
针对练习
如图,某办公大楼正前方有一根高度是15 m的旗杆ED,从办公楼顶端A测得旗杆顶端E 的俯角α 是45°,旗杆底端D到大楼前梯坎底边的距离DC 是20 m,梯坎坡长BC 是12 m,梯坎坡度i=
1∶ ,则大楼AB 的高度约为(精确到0.1米,参
考数据: ≈1.41, ≈1.73, ≈2.45)( )
A.30.6 m
B.32.1 m
C.37.9 m
D.39.4 m
D
针对练习
1.从一艘船上测得海岸_上高为42米的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )
A.42米 B.14米 C.21米 D.42米.
2.身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
A.甲 B.乙 C.丙 D.丁
A
D
课堂练习
3.如图,某航天飞船在地球表面点P的正上方A处,从A处观测到地球表面的最远点Q,若∠QAP=a,地球半径为R,则航天飞船距离地球表面的最近距离AP以及P,Q两点间的地面距离分别是( )
A. B.
C. D.
B
课堂练习
4.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BC0=x,则点A到OC的距离等于( )
A. a·sinx+b·sinx
B. a·cosx+b·cosx
C. a·sinx+b·cosx
D. a·cosx+b·sinx
D
课堂练习
5.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为
_________m.(结果保留根号)
6.如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影子约为10米,则大树的高约为______米. (结果保留根号)
5+5
1
课堂练习
7.某公共场所准备改善原有楼梯的安全性能,把倾角由45°减至30°,楼梯高度不变.已知楼梯原长4m,那么调整的楼梯.会增加多长 楼梯多占了多长一段地面
解:在Rt△ABC中,AB=4,∠ABC=45°
∴BC=AC=AB·sin45°=2m
在Rt△ADC中,AC=2,∠ADC=30°
∴AD= m,DC= m
∴AD-AB=(4-4)m,DC-BC=(2-2)m
答:调整后楼梯会增加(4-4)m,占地会加长(2-2)m.
课堂练习
8.如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m)
解:在Rt△ACD中,∠A=30°
∴tan30 °= ∴AC=CD
在Rt△BCD中,∠CBD=60°
∴tan60°= ,∴BC=CD
∵AC-BC=50,∴CD-CD=50 解得,CD≈43
答:该塔约为43m高.
课堂练习
9.为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE=10m,其坡度为i1=1:,将步梯DE改造为斜坡AF,其坡度为i2=1:4,求斜坡AF的长度(结果精确到0.01m,参考数据: ≈1.732, ≈4.123).
课堂练习
解:∵DE=10m,其坡度为i1=1:
∴CE=CD
由勾股定理得 ,解得CD=5m
∵四边形ABCD为矩形,∴AB=CD=5m
∵斜坡AF的坡度为i2=1:4
∴
∴BF=4AB=20m
在Rt△ABF中,
故斜坡AF的长度约为20.62m.
课堂练习
10.八仙阁是八仙山公园里的一个主景区,八仙阁也是晋江的一个标志性建筑.在阁楼上可以看到整个八仙山公园全景,甚至周围景观都能尽收眼底.小明想知道它的高度.于是走到点C处,测得此时塔尖A的仰角是37,向前走了15.5米至点F处,测得此时塔尖A的仰角是,已知小明的眼睛离地面高度是1.5米,请聪明的你帮他求出八仙阁AB的高度.(参考数据:,,)
课堂练习
9.八仙阁是八仙山公园里的一个主景区,八仙阁也是晋江的一个标志性建筑.在阁楼上可以看到整个八仙山公园全景,甚至周围景观都能尽收眼底.小明想知道它的高度.于是走到点C处,测得此时塔尖A的仰角是37,向前走了15.5米至点F处,测得此时塔尖A的仰角是,已知小明的眼睛离地面高度是1.5米,请聪明的你帮他求出八仙阁AB的高度.(参考数据:,,)
解:由题意得,,
则四边形均为矩形.
所以米,米,
在中,,则.设米,
课堂练习
9.八仙阁是八仙山公园里的一个主景区,八仙阁也是晋江的一个标志性建筑.在阁楼上可以看到整个八仙山公园全景,甚至周围景观都能尽收眼底.小明想知道它的高度.于是走到点C处,测得此时塔尖A的仰角是37,向前走了15.5米至点F处,测得此时塔尖A的仰角是,已知小明的眼睛离地面高度是1.5米,请聪明的你帮他求出八仙阁AB的高度.(参考数据:,,)
在中,,
则,即,
解得:,
所以米,
则(米).
答:八仙阁AB的高度为48米.
课堂练习
感谢观看
