第七章三角形导学案
图片预览
文档简介
第七章《三角形》复习导学案
学习目标:
1、能说出三角形三边之间的关系和一个三角形的高、中线、角平分线及其定义,对于任意一个三角形,会画出它的中线,角平分线和高线;
2、记住三角形的内角和定理及其推论;知道三角形的外角的概念及外角和;会用多边形的内角和公式及外角和计算。
一、知识梳理,形成框架
学生看书完成以下知识梳理
1、三角形的高、中线、角平分线
(1)三角形的高、中线、角平分线都是 (选填‘线段、射线和直线’)
(2)交点情况
a.三条高所在的直线交于一点:锐角三角形时交点位于三角形的 ;直角三角形时,交点位于直角三角形的 ;钝角三角形的交点位于三角形的 。
b. 三角形的三条中线交于一点,交点位于三角形的内 ,是三角形的重心。每条中线都把三角形分成 相等的两个三角形。
c.三角形的三条角平分线交于一点,交点位于三角形的 ,是三角形的内心。
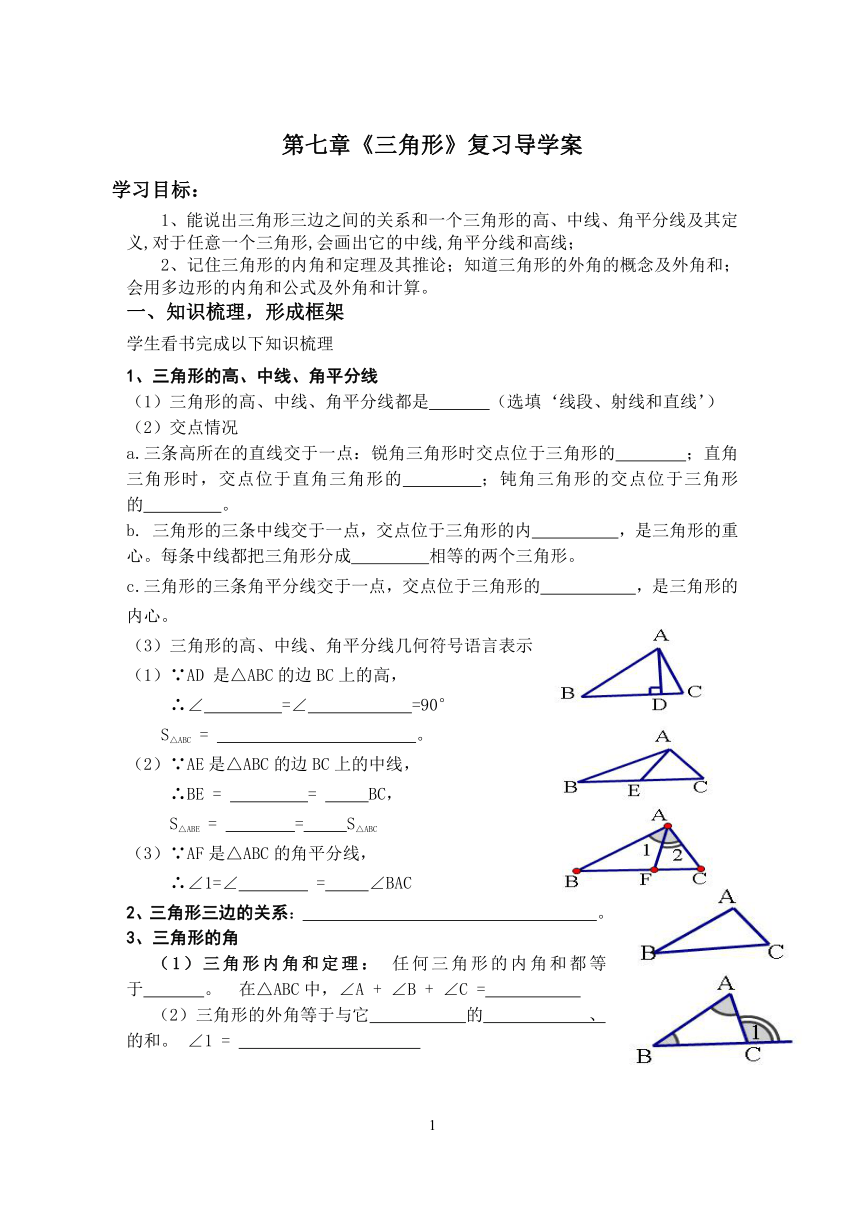
(3)三角形的高、中线、角平分线几何符号语言表示
(1)∵AD 是△ABC的边BC上的高,
∴∠ =∠ =90°
S△ABC = 。
(2)∵AE是△ABC的边BC上的中线,
∴BE = = BC,
S△ABE = = S△ABC
(3)∵AF是△ABC的角平分线,
∴∠1=∠ = ∠BAC
2、三角形三边的关系: 。
3、三角形的角
(1)三角形内角和定理: 任何三角形的内角和都等于 。 在△ABC中,∠A + ∠B + ∠C =
(2)三角形的外角等于与它 的 、 的和。 ∠1 =
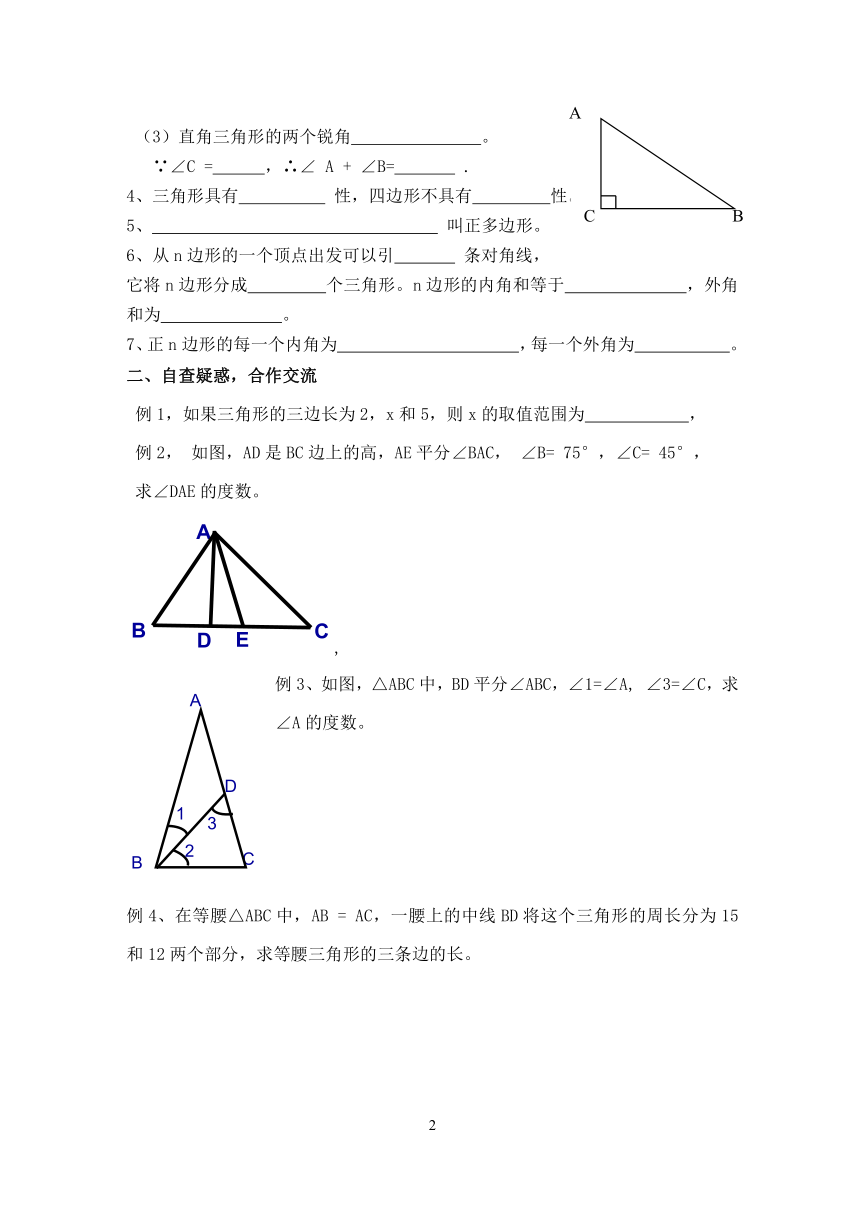
(3)直角三角形的两个锐角 。
∵∠C = ,∴∠ A + ∠B= .
4、三角形具有 性,四边形不具有 性。
5、 叫正多边形。
6、从n边形的一个顶点出发可以引 条对角线,
它将n边形分成 个三角形。n边形的内角和等于 ,外角和为 。
7、正n边形的每一个内角为 ,每一个外角为 。
二、自查疑惑,合作交流
例1,如果三角形的三边长为2,x和5,则x的取值范围为 ,
例2, 如图,AD是BC边上的高,AE平分∠BAC, ∠B= 75°,∠C= 45°,
求∠DAE的度数。
,
例3、如图,△ABC中,BD平分∠ABC,∠1=∠A, ∠3=∠C,求∠A的度数。
例4、在等腰△ABC中,AB = AC,一腰上的中线BD将这个三角形的周长分为15和12两个部分,求等腰三角形的三条边的长。
三、重点题型,集中再现
1、如果三角形的两边长为6和2,且第三边为偶数,则第三边的长是 .
2、(1)等腰三角形两边是1和5,则周长是
(2)等腰三角形两边是3和5,则周长是
3、已知等腰三角形的两边长为a、b,且满足∣a-3∣+=0,则这个等腰三角形的周长是
4、一个多边形的内角和是1980°,则它的边数是____,共有条对角线____,它的外角和是____。
5、如图,在△ABC中,AD⊥BC,CE是△ABC的角平分线,AD、CE交于F点.当
∠BAC=80°,∠B=40°时,求∠ACB、∠AEC、∠AFE的度数.
6、一个正多边形,若它的一个外角与相邻的内角的度数比为1:4,求这个多边形的内角和。
四、当堂训练,分层达标
1.下列长度的三条线段能组成三角形的是 ( )
A.1cm 2cm 3cm B.6cm 2cm 3cm
C 4cm 6cm 8cm D.5cm 12cm 6cm
2.已知:如图,Rt△ABC中,∠ACB=900,DE过点C,且DE//AB,若∠ACD=550,则∠B的度数为 ( )
A.350 B.450
C.300 D.550
3.如图所示:AB//CD,∠A=450,∠C=290,则∠E=_____
第3题 第4题 第7题
4.如图,将一个长方形纸片按如图方法折叠,BC、BD为折痕,则∠CBD=____
5.一个多边形的每个内角都等于1500,则这个多边形是_____边形.
6.如果一个三角形的两边长分别是2cm和7cm,且第三边为奇数,则三角形的周长是 cm.
7.如右图,∠A=600,∠B=800,则.∠2+∠1=_____.
8.如图,在△ABC中:(1)画出BC边上的高AD和中线AE;
(2)若∠B=300,∠ACB=1300, 求∠BAD和∠CAD的度数。
C
B
A
A
B
D
E
C
3
1
2
B
A
C
D
PAGE
4
学习目标:
1、能说出三角形三边之间的关系和一个三角形的高、中线、角平分线及其定义,对于任意一个三角形,会画出它的中线,角平分线和高线;
2、记住三角形的内角和定理及其推论;知道三角形的外角的概念及外角和;会用多边形的内角和公式及外角和计算。
一、知识梳理,形成框架
学生看书完成以下知识梳理
1、三角形的高、中线、角平分线
(1)三角形的高、中线、角平分线都是 (选填‘线段、射线和直线’)
(2)交点情况
a.三条高所在的直线交于一点:锐角三角形时交点位于三角形的 ;直角三角形时,交点位于直角三角形的 ;钝角三角形的交点位于三角形的 。
b. 三角形的三条中线交于一点,交点位于三角形的内 ,是三角形的重心。每条中线都把三角形分成 相等的两个三角形。
c.三角形的三条角平分线交于一点,交点位于三角形的 ,是三角形的内心。
(3)三角形的高、中线、角平分线几何符号语言表示
(1)∵AD 是△ABC的边BC上的高,
∴∠ =∠ =90°
S△ABC = 。
(2)∵AE是△ABC的边BC上的中线,
∴BE = = BC,
S△ABE = = S△ABC
(3)∵AF是△ABC的角平分线,
∴∠1=∠ = ∠BAC
2、三角形三边的关系: 。
3、三角形的角
(1)三角形内角和定理: 任何三角形的内角和都等于 。 在△ABC中,∠A + ∠B + ∠C =
(2)三角形的外角等于与它 的 、 的和。 ∠1 =
(3)直角三角形的两个锐角 。
∵∠C = ,∴∠ A + ∠B= .
4、三角形具有 性,四边形不具有 性。
5、 叫正多边形。
6、从n边形的一个顶点出发可以引 条对角线,
它将n边形分成 个三角形。n边形的内角和等于 ,外角和为 。
7、正n边形的每一个内角为 ,每一个外角为 。
二、自查疑惑,合作交流
例1,如果三角形的三边长为2,x和5,则x的取值范围为 ,
例2, 如图,AD是BC边上的高,AE平分∠BAC, ∠B= 75°,∠C= 45°,
求∠DAE的度数。
,
例3、如图,△ABC中,BD平分∠ABC,∠1=∠A, ∠3=∠C,求∠A的度数。
例4、在等腰△ABC中,AB = AC,一腰上的中线BD将这个三角形的周长分为15和12两个部分,求等腰三角形的三条边的长。
三、重点题型,集中再现
1、如果三角形的两边长为6和2,且第三边为偶数,则第三边的长是 .
2、(1)等腰三角形两边是1和5,则周长是
(2)等腰三角形两边是3和5,则周长是
3、已知等腰三角形的两边长为a、b,且满足∣a-3∣+=0,则这个等腰三角形的周长是
4、一个多边形的内角和是1980°,则它的边数是____,共有条对角线____,它的外角和是____。
5、如图,在△ABC中,AD⊥BC,CE是△ABC的角平分线,AD、CE交于F点.当
∠BAC=80°,∠B=40°时,求∠ACB、∠AEC、∠AFE的度数.
6、一个正多边形,若它的一个外角与相邻的内角的度数比为1:4,求这个多边形的内角和。
四、当堂训练,分层达标
1.下列长度的三条线段能组成三角形的是 ( )
A.1cm 2cm 3cm B.6cm 2cm 3cm
C 4cm 6cm 8cm D.5cm 12cm 6cm
2.已知:如图,Rt△ABC中,∠ACB=900,DE过点C,且DE//AB,若∠ACD=550,则∠B的度数为 ( )
A.350 B.450
C.300 D.550
3.如图所示:AB//CD,∠A=450,∠C=290,则∠E=_____
第3题 第4题 第7题
4.如图,将一个长方形纸片按如图方法折叠,BC、BD为折痕,则∠CBD=____
5.一个多边形的每个内角都等于1500,则这个多边形是_____边形.
6.如果一个三角形的两边长分别是2cm和7cm,且第三边为奇数,则三角形的周长是 cm.
7.如右图,∠A=600,∠B=800,则.∠2+∠1=_____.
8.如图,在△ABC中:(1)画出BC边上的高AD和中线AE;
(2)若∠B=300,∠ACB=1300, 求∠BAD和∠CAD的度数。
C
B
A
A
B
D
E
C
3
1
2
B
A
C
D
PAGE
4
