变量的相关关系(浙江省嘉兴市)
文档属性
| 名称 | 变量的相关关系(浙江省嘉兴市) |

|
|
| 格式 | rar | ||
| 文件大小 | 129.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-27 09:25:00 | ||
图片预览




文档简介
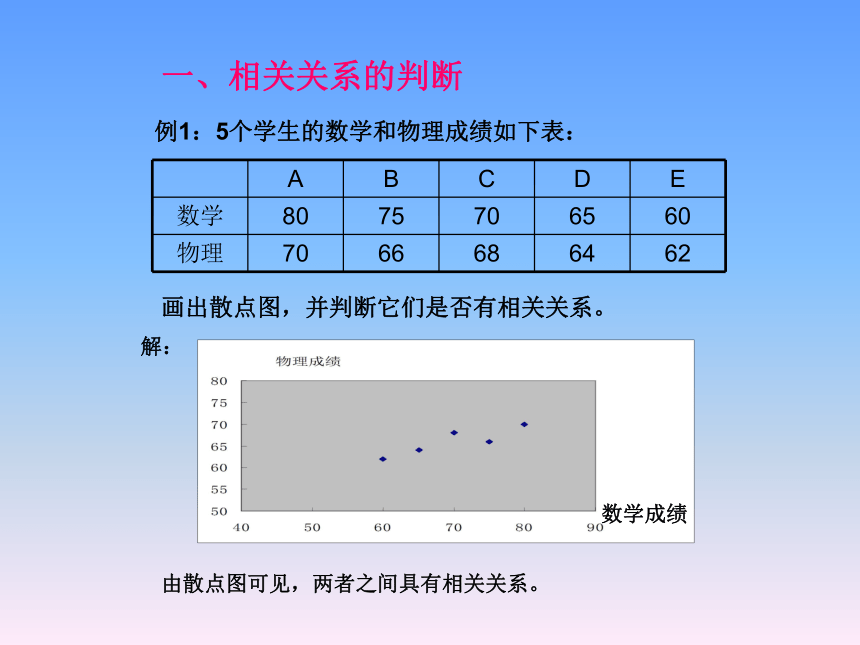
课件21张PPT。变量间的相关关系2007 10 12桐乡二中“如果你的数学成绩好,那么你的物理学习就不会有什么大问题”你如何认识学生的数学成绩与物理成绩之间存在的关系?不能通过一个人的数学成绩来确定他的物理成绩,两个变量之间是一种不确定关系。数学成绩物理成绩学习兴趣学习时间其他因素两个变量的相关关系:(1)定义:当自变量取值一定,因变量的取值带有一定的随机性时,两个变量之间 的关系称为相关关系。相关关系是一种非确定性关系。(2)相关关系与函数关系的异同点:不同点:①函数关系是一种确定性关系;相关关系是一种非确定性关系。②函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系。如:在校儿童脚的大小与阅读能力有很强的相关关系,但不是因果关系。联系:两者均是指两个变量的关系;在一定条件下可以相互转化。一、相关关系的判断例1:5个学生的数学和物理成绩如下表:画出散点图,并判断它们是否有相关关系。解:数学成绩由散点图可见,两者之间具有相关关系。例1:下列各关系中具有相关关系的是( )
(A)正方体的体积与边长;(B)匀速行驶的车辆的行驶距离与时间;
(C)人的身高与体重; (D)人的身高与视力C例2:下列各关系中,不属于相关关系的是( )
(A)名师出高徒;(B)球的表面积与体积;(C)家庭的支出与收入
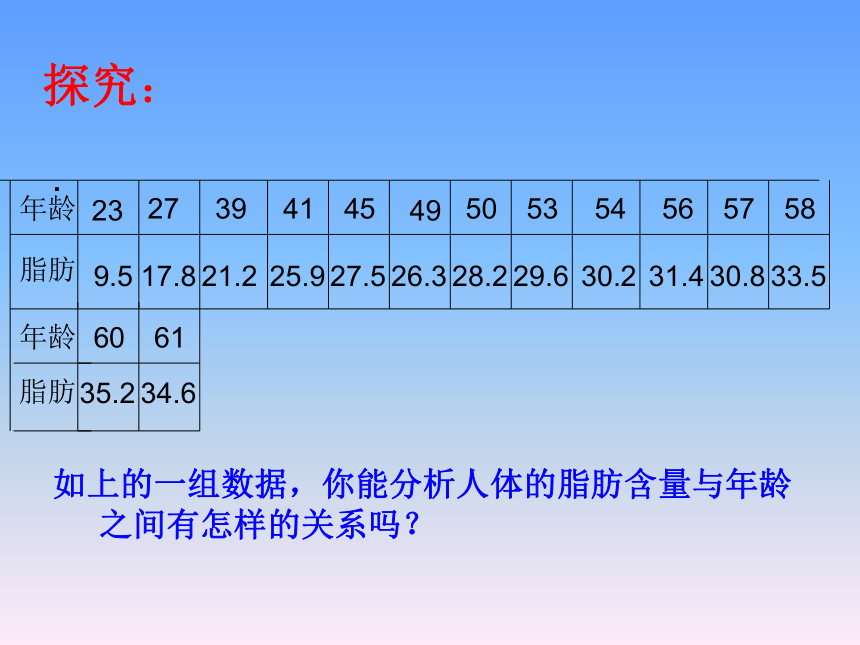
(D)人的年龄与体重B(3)相关关系的分析方向由于相关关系的不确定性,在寻找变量相关关系的过程中,统计具有非常重要的作用。我们可以通过收集大量的数据,在对数据进行统计分析的基础上,发现其中的规律,对他们的关系作出判断。探究:.年龄脂肪239.52717.83921.24125.9454927.526.35028.25329.65430.25631.45730.8年龄脂肪5833.56035.26134.6如上的一组数据,你能分析人体的脂肪含量与年龄
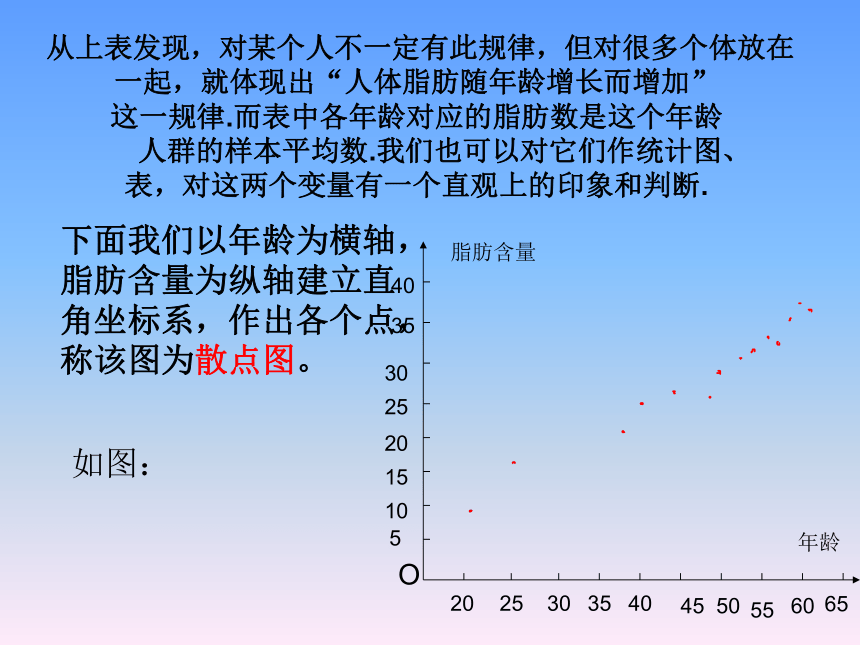
之间有怎样的关系吗? 从上表发现,对某个人不一定有此规律,但对很多个体放在一起,就体现出“人体脂肪随年龄增长而增加” 这一规律.而表中各年龄对应的脂肪数是这个年龄 人群的样本平均数.我们也可以对它们作统计图、 表,对这两个变量有一个直观上的印象和判断. 下面我们以年龄为横轴,
脂肪含量为纵轴建立直
角坐标系,作出各个点,
称该图为散点图。如图:O20253035404550556065年龄脂肪含量510152025303540从刚才的散点图发现:年龄越大,体内脂肪含量越高,点的位置散布在从左下角到右上角的区域。称它们成正相关。 但有的两个变量的相关,如下图所示:如高原含氧量与海拔高度
的相关关系,海平面以上,
海拔高度越高,含氧量越
少。
作出散点图发现,它们散
布在从左上角到右下角的区
域内。又如汽车的载重和汽
车每消耗1升汽油所行使的
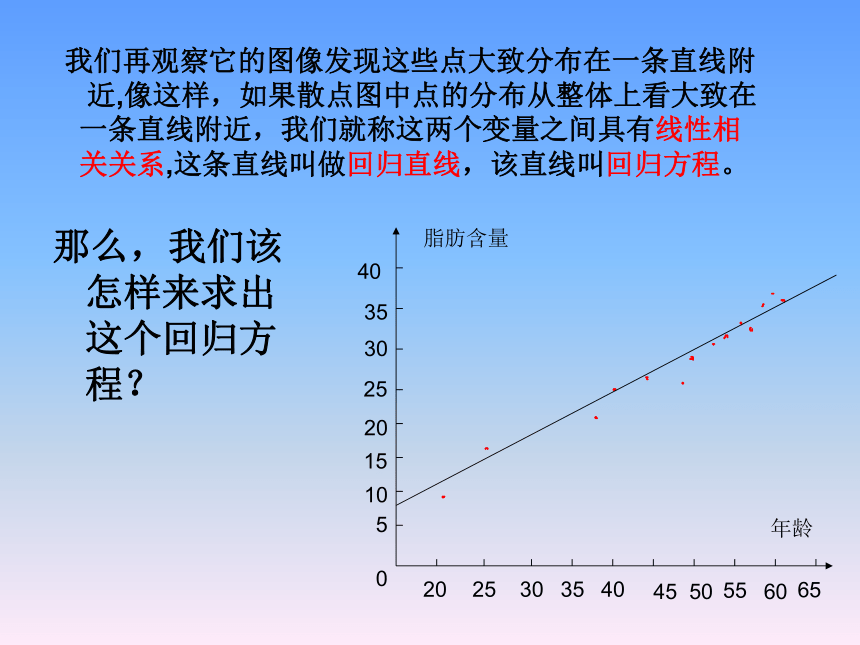
平均路程,称它们成负相关.注:可考虑让学生思考书P86的思考.O我们再观察它的图像发现这些点大致分布在一条直线附 近,像这样,如果散点图中点的分布从整体上看大致在 一条直线附近,我们就称这两个变量之间具有线性相 关关系,这条直线叫做回归直线,该直线叫回归方程。那么,我们该怎样来求出这个回归方程?20253035404550556065年龄脂肪含量0510152025303540注意!(1)若所有样本点都落在某函数曲线上,则两变量之间是一种确定性关系,用函数关系表示。(2)若所有样本点都落在某一函数曲线附近,则变量之间具有相关关系。(3)若所有样本点都落在某一直线附近,变量之间就具有线性相关关系。该直线称为回归直线。线性回归方程思考?你认为回归直线具有怎样的特征?应当如何求回归直线的方程呢?(1)特征:假设样本点为(2)如何求出这个回归方程?对于单变量样本数据而言,平均数是样本数据的中心,类似地,对双变量样本点而言,回归直线是样本点的中心。探究回归直线一定过这一点:由探究可知,求回归方程的关键是如何用数学的方法刻画“从整体上看,各点与此直线的距离最小”?设已经得到具有线性相关关系的变量的一组数据:设所求回归方程是:1.以上公式的推导较复杂,故不作推导,但它的原理较为简单:即各点到该直线的距离的平方和最小,这一方法叫最小二乘法。(参看如书P89)2.其中,b是回归方程的斜率,表示x每增加一个单位, 增加b个单位;a是截距,表示方程中不受x影响的部分。二、求线性回归方程例2:观察两相关变量得如下表:求两变量间的回归方程解1:列表:计算得:小结:求线性回归直线方程的步骤:
第一步:列表 ;
第二步:计算 ;
第三步:代入公式计算b,a的值;
第四步:写出直线方程。例:有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:摄氏温度 -5 0 4 7 12 15 19 23 27 31 36热饮杯数 156 150 132 128 130 116 104 89 93 76 54 (1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一
般规律;
(3)求回归方程;
(4)如果某天的气温是 C,预测这天卖出的热饮杯数。三、利用线性回归方程对总体进行估计解: (1)散点图(2)气温与热饮杯数成负相关,即气温越高, 卖出去的热饮杯数越少。(3)从散点图可以看出,这些点大致分布在一条直线附近。小结:
(1)判断变量之间有无相关关系,简便方法就是画散点图。
(2)当数字少时,可用人工或计算器,求回归方程;当数字多时,用Excel求回归方程。
(3)利用回归方程,可以进行预测。练习1、某种产品的广告费支出x与销售额y(单位:百万元)之间有如下的对应数据:(1)画出散点图;(2)求线性回归方程;(3)预测当广告费支出7(百万元)时的销售额。作业:1.《导与练》第59~62页
2.课本 第94~95页
(A)正方体的体积与边长;(B)匀速行驶的车辆的行驶距离与时间;
(C)人的身高与体重; (D)人的身高与视力C例2:下列各关系中,不属于相关关系的是( )
(A)名师出高徒;(B)球的表面积与体积;(C)家庭的支出与收入
(D)人的年龄与体重B(3)相关关系的分析方向由于相关关系的不确定性,在寻找变量相关关系的过程中,统计具有非常重要的作用。我们可以通过收集大量的数据,在对数据进行统计分析的基础上,发现其中的规律,对他们的关系作出判断。探究:.年龄脂肪239.52717.83921.24125.9454927.526.35028.25329.65430.25631.45730.8年龄脂肪5833.56035.26134.6如上的一组数据,你能分析人体的脂肪含量与年龄
之间有怎样的关系吗? 从上表发现,对某个人不一定有此规律,但对很多个体放在一起,就体现出“人体脂肪随年龄增长而增加” 这一规律.而表中各年龄对应的脂肪数是这个年龄 人群的样本平均数.我们也可以对它们作统计图、 表,对这两个变量有一个直观上的印象和判断. 下面我们以年龄为横轴,
脂肪含量为纵轴建立直
角坐标系,作出各个点,
称该图为散点图。如图:O20253035404550556065年龄脂肪含量510152025303540从刚才的散点图发现:年龄越大,体内脂肪含量越高,点的位置散布在从左下角到右上角的区域。称它们成正相关。 但有的两个变量的相关,如下图所示:如高原含氧量与海拔高度
的相关关系,海平面以上,
海拔高度越高,含氧量越
少。
作出散点图发现,它们散
布在从左上角到右下角的区
域内。又如汽车的载重和汽
车每消耗1升汽油所行使的
平均路程,称它们成负相关.注:可考虑让学生思考书P86的思考.O我们再观察它的图像发现这些点大致分布在一条直线附 近,像这样,如果散点图中点的分布从整体上看大致在 一条直线附近,我们就称这两个变量之间具有线性相 关关系,这条直线叫做回归直线,该直线叫回归方程。那么,我们该怎样来求出这个回归方程?20253035404550556065年龄脂肪含量0510152025303540注意!(1)若所有样本点都落在某函数曲线上,则两变量之间是一种确定性关系,用函数关系表示。(2)若所有样本点都落在某一函数曲线附近,则变量之间具有相关关系。(3)若所有样本点都落在某一直线附近,变量之间就具有线性相关关系。该直线称为回归直线。线性回归方程思考?你认为回归直线具有怎样的特征?应当如何求回归直线的方程呢?(1)特征:假设样本点为(2)如何求出这个回归方程?对于单变量样本数据而言,平均数是样本数据的中心,类似地,对双变量样本点而言,回归直线是样本点的中心。探究回归直线一定过这一点:由探究可知,求回归方程的关键是如何用数学的方法刻画“从整体上看,各点与此直线的距离最小”?设已经得到具有线性相关关系的变量的一组数据:设所求回归方程是:1.以上公式的推导较复杂,故不作推导,但它的原理较为简单:即各点到该直线的距离的平方和最小,这一方法叫最小二乘法。(参看如书P89)2.其中,b是回归方程的斜率,表示x每增加一个单位, 增加b个单位;a是截距,表示方程中不受x影响的部分。二、求线性回归方程例2:观察两相关变量得如下表:求两变量间的回归方程解1:列表:计算得:小结:求线性回归直线方程的步骤:
第一步:列表 ;
第二步:计算 ;
第三步:代入公式计算b,a的值;
第四步:写出直线方程。例:有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:摄氏温度 -5 0 4 7 12 15 19 23 27 31 36热饮杯数 156 150 132 128 130 116 104 89 93 76 54 (1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一
般规律;
(3)求回归方程;
(4)如果某天的气温是 C,预测这天卖出的热饮杯数。三、利用线性回归方程对总体进行估计解: (1)散点图(2)气温与热饮杯数成负相关,即气温越高, 卖出去的热饮杯数越少。(3)从散点图可以看出,这些点大致分布在一条直线附近。小结:
(1)判断变量之间有无相关关系,简便方法就是画散点图。
(2)当数字少时,可用人工或计算器,求回归方程;当数字多时,用Excel求回归方程。
(3)利用回归方程,可以进行预测。练习1、某种产品的广告费支出x与销售额y(单位:百万元)之间有如下的对应数据:(1)画出散点图;(2)求线性回归方程;(3)预测当广告费支出7(百万元)时的销售额。作业:1.《导与练》第59~62页
2.课本 第94~95页
