2014-2015学年度第一学期期末质量检测初四数学模拟试题
文档属性
| 名称 | 2014-2015学年度第一学期期末质量检测初四数学模拟试题 | 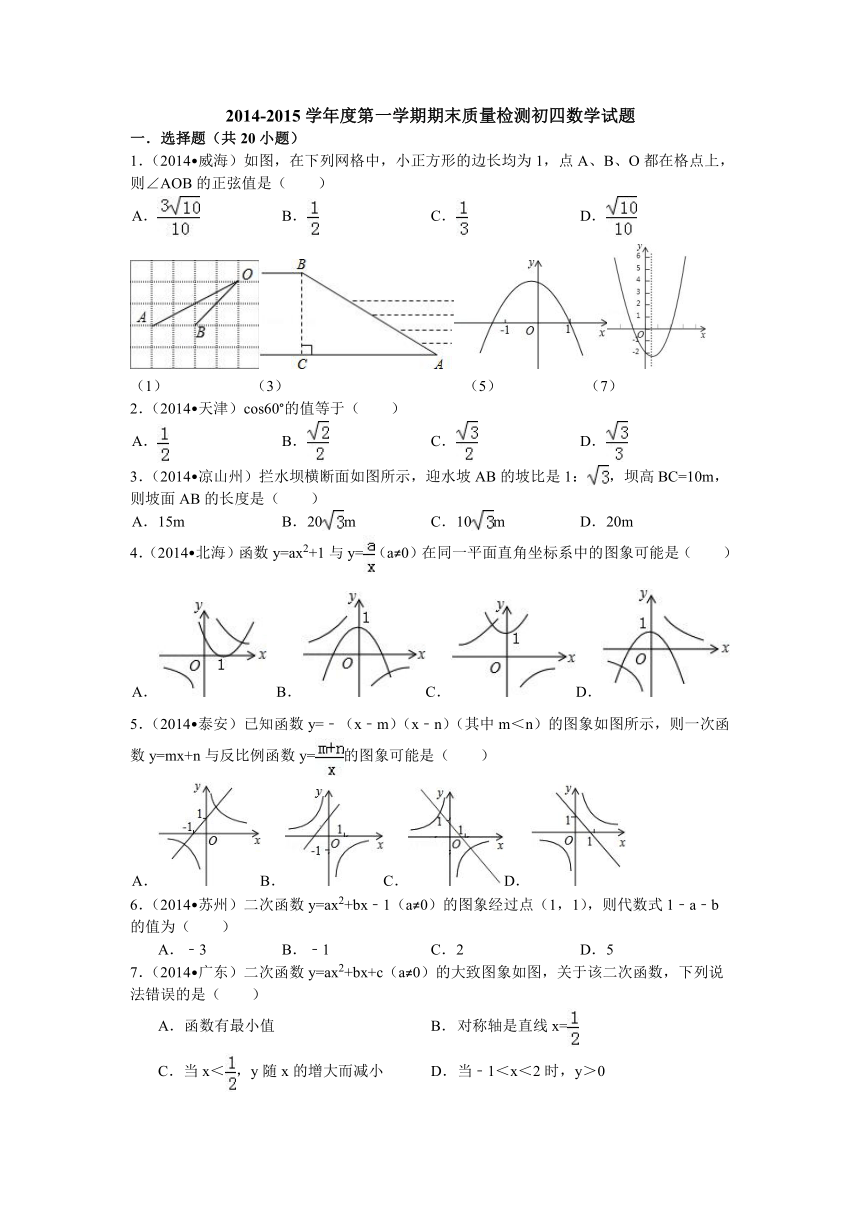 | |
| 格式 | zip | ||
| 文件大小 | 222.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-04 16:36:17 | ||
图片预览


文档简介
2014-2015学年度第一学期期末质量检测初四数学试题
一.选择题(共20小题)
1.(2014 威海)如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A. B. C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (3) (5) (7)
2.(2014 天津)cos60°的值等于( )
A. B. C. D.
3.(2014 凉山州)拦水坝横断面如图所示,迎水坡AB的坡比是1:,坝高BC=10m,则坡面AB的长度是( )
A.15m B. 20m C. 10m D. 20m
4.(2014 北海)函数y=ax2+1与y=(a≠0)在同一平面直角坐标系中的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
5.(2014 泰安)已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com )D. ( http: / / www.21cnjy.com )
6.(2014 苏州)二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则代数式1﹣a﹣b的值为( )
A.﹣3 B. ﹣1 C. 2 D. 5
7.(2014 广东)二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
A.函数有最小值 B. 对称轴是直线x=
C.当x<,y随x的增大而减小 D. 当﹣1<x<2时,y>0
8.(2014 哈尔滨)将抛物线y=﹣2x2+1向右平移1个单位,再向上平移2个单位后所得到的抛物线为( )
A.y=﹣2(x+1)2﹣1 B.y=﹣2(x+1)2+3 C.y=﹣2(x﹣1)2+1 D. y=﹣2(x﹣1)2+3
9.(2014 路南区三模)用配方法求抛物线y=x2﹣4x+1的顶点坐标,配方后的结果是( )
A. y=(x﹣2)2﹣3 B. y=(x+2)2﹣3 C. y=(x﹣2)2﹣5 D. y=(x+2)2﹣5
10.(2014 锦州)二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象如图,ax2+bx+c=m有实数根的条件是( )
A. m≥﹣2 B. m≥5 C. m≥0 D. m>4
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(10) (13) (14) (15)
11.(2014 凉山州)下列图形中阴影部分的面积相等的是( )
( http: / / www.21cnjy.com )
A. ②③ B. ③④ C. ①② D. ①④
12.(2014 台州)从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是( )
A.B.C.D.
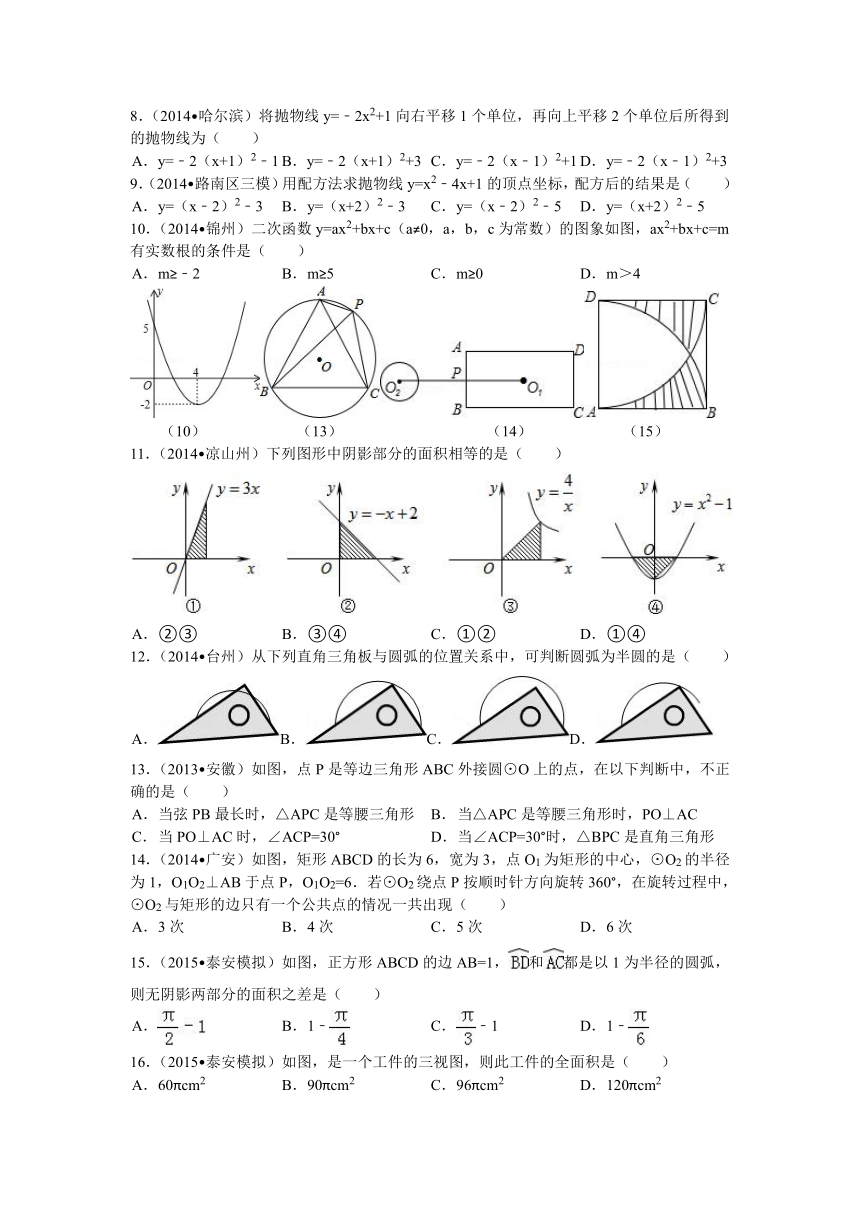
13.(2013 安徽)如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是( )
A. 当弦PB最长时,△APC是等腰三角形 B. 当△APC是等腰三角形时,PO⊥AC
C. 当PO⊥AC时,∠ACP=30° D. 当∠ACP=30°时,△BPC是直角三角形
14.(2014 广安)如图,矩形ABC ( http: / / www.21cnjy.com )D的长为6,宽为3,点O1为矩形的中心,⊙O2的半径为1,O1O2⊥AB于点P,O1O2=6.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边只有一个公共点的情况一共出现( )
A. 3次 B. 4次 C. 5次 D. 6次
15.(2015 泰安模拟)如图,正方形ABCD的边AB=1,和都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
A. B. 1﹣ C. ﹣1 D. 1﹣
16.(2015 泰安模拟)如图,是一个工件的三视图,则此工件的全面积是( )
A. 60πcm2 B. 90πcm2 C. 96πcm2 D. 120πcm2
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(16) (19) (20)
17.(2014 石家庄一模)如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是( )
A. ①②③④ B. ④①③② C. ④②③① D. ④③②①
18.(2014 路南区三模)向上发射一枚 ( http: / / www.21cnjy.com )炮弹,经x秒后的高度为y公尺,且时间与高度关系为y=ax2+bx.若此炮弹在第7秒与第14秒时的高度相等,则在下列哪一个时间的高度是最高的( )
A. 第9.5秒 B. 第10秒 C. 第10.5秒 D. 第11秒
19.(2014 哈尔滨)如图,AB是⊙O ( http: / / www.21cnjy.com )的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是( )
A. 30° B. 25° C. 20° D. 15°
20.(2014 义乌市) ( http: / / www.21cnjy.com )一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A. 5:4 B. 5:2 C. :2 D. :
二.填空题(共5小题)
21.(2014 包头)如图,AB是⊙O的直径,BC是弦,点E是的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为 _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(21) (22)
22.画出几何体的俯视图、左视图.
23.(2014 攀枝花)在△ABC中,如果∠A、∠B满足|tanA﹣1|+(cosB﹣)2=0,那么∠C= .
24.(2014 牡丹江)抛物线y=ax2+bx+c经过点A(﹣3,0),对称轴是直线x=﹣1,则a+b+c= .
25.(2014 扬州)如图,抛物线y ( http: / / www.21cnjy.com )=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a﹣2b+c的值为 _________ .
三.解答题(共5小题)
26.(2014 丹东)在2014 ( http: / / www.21cnjy.com )年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x(x≥60)元,销售量为y套.
(1)求出y与x的函数关系式.
(2)当销售单价为多少元时,月销售额为14000元;
(3)当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少?
27.(2015 泰安模拟)甲、乙 ( http: / / www.21cnjy.com )两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.
( http: / / www.21cnjy.com )
28.(2014 泰安)二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
29.(2014 长沙)如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O的切线交AC于点E.
(1)求证:DE⊥AC;
(2)若AB=3DE,求tan∠ACB的值.
( http: / / www.21cnjy.com )
30.(2014 白银)如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
( http: / / www.21cnjy.com )
参考答案
一.选择题(共20小题)
1.D.2.A.3.D.4.B.5.C.6.B.7.D.8.D.9.A.10.A.
11.A.12.B.13.C.14.B.15.A.16.C.17.B.18.C.19.B.20.A.
填空题(共5小题)
8 .22. ( http: / / www.21cnjy.com )
23.75° .24. 0 25. 0 .
三.解答题(共5小题)
26.解:(1),∴y=﹣4x+480;
(2)根据题意可得,x(﹣4x+480)=14000,解得,x1=70,x2=50(不合题意舍去),
∴当销售价为70元时,月销售额为14000元.
(3)设一个月内获得的利润为w元,根据题意,得w=(x﹣40)(﹣4x+480),
=﹣4x2+640x﹣19200,=﹣4(x﹣80)2+6400,
当x=80时,w的最大值为6400
∴当销售单价为80元时,才能在一个月内获得最大利润,最大利润是6400元.
27.解:(1)作BD⊥AC于点D,如图所示:
由题意可知:AB=30×1=30海里,∠BAC=30°,∠BCA=45°,
在Rt△ABD中,
∵AB=30海里,∠BAC=30°,∴BD=15海里,AD=ABcos30°=15海里,
在Rt△BCD中,
∵BD=15海里,∠BCD=45°,∴CD=15海里,BC=15海里,
∴AC=AD+CD=15+15海里,
即A、C间的距离为(15+15)海里.
(2)∵AC=15+15(海里),轮船乙从A到C的时间为=+1,
由B到C的时间为+1﹣1=,
∵BC=15海里,∴轮船甲从B到C的速度为=5(海里/小时).
28.解:(1)由直线y=﹣x+1可知A(0,1),B(﹣3,),又点(﹣1,4)经过二次函数,
根据题意得: ( http: / / www.21cnjy.com ),解得:,则二次函数的解析式是:y=﹣﹣x+1;
(2)设N(x,﹣x2﹣x+1),则M(x,﹣x+1),P(x,0).∴MN=PN﹣PM
=﹣x2﹣x+1﹣(﹣x+1)=﹣x2﹣x=﹣(x+)2+,
则当x=﹣时,MN的最大值为;
(3)连接MN、BN、BM与NC互相垂直平分,即四边形BCMN是菱形,
由于BC∥MN,即MN=BC,且BC=MC,即﹣x2﹣x=,
且(﹣x+1)2+(x+3)2=,
解得:x=﹣1或x=﹣2(不合题意舍去),
故当N(﹣1,4)时,BM和NC互相垂直平分.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(27) (28) (29) (30)
29.(1)证明:连接OD,
∵D是BC的中点,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,
∵DE是⊙O的切线,∴OD⊥DE,∴DE⊥AC;
(2)解:连接AD,∵AB是⊙O的直径,∴∠ADB=90°,
∵DE⊥AC,∴∠ADC=∠DEC=∠AED=90°,∴∠ADE=∠DCE
在△ADE和△CDE中,∴△CDE∽△DAE,∴,
设tan∠ACB=x,CE=a,则DE=ax,AC=3ax,AE=3ax﹣a,
∴,整理得:x2﹣3x+1=0,解得:x=,∴tan∠ACB=.
30.(1)证明:连接OD,OE,∵AB为圆O的直径,∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,∴DE=BE,
在△OBE和△ODE中,,∴△OBE≌△ODE(SSS),∴∠ODE=∠ABC=90°,
则DE为圆O的切线;
(2)在Rt△ABC中,∠BAC=30°,∴BC=AC,∵BC=2DE=4,∴AC=8,
又∵∠C=60°,DE=CE,
∴△DEC为等边三角形,即DC=DE=2,则AD=AC﹣DC=6.
一.选择题(共20小题)
1.(2014 威海)如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A. B. C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (3) (5) (7)
2.(2014 天津)cos60°的值等于( )
A. B. C. D.
3.(2014 凉山州)拦水坝横断面如图所示,迎水坡AB的坡比是1:,坝高BC=10m,则坡面AB的长度是( )
A.15m B. 20m C. 10m D. 20m
4.(2014 北海)函数y=ax2+1与y=(a≠0)在同一平面直角坐标系中的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
5.(2014 泰安)已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com )D. ( http: / / www.21cnjy.com )
6.(2014 苏州)二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则代数式1﹣a﹣b的值为( )
A.﹣3 B. ﹣1 C. 2 D. 5
7.(2014 广东)二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
A.函数有最小值 B. 对称轴是直线x=
C.当x<,y随x的增大而减小 D. 当﹣1<x<2时,y>0
8.(2014 哈尔滨)将抛物线y=﹣2x2+1向右平移1个单位,再向上平移2个单位后所得到的抛物线为( )
A.y=﹣2(x+1)2﹣1 B.y=﹣2(x+1)2+3 C.y=﹣2(x﹣1)2+1 D. y=﹣2(x﹣1)2+3
9.(2014 路南区三模)用配方法求抛物线y=x2﹣4x+1的顶点坐标,配方后的结果是( )
A. y=(x﹣2)2﹣3 B. y=(x+2)2﹣3 C. y=(x﹣2)2﹣5 D. y=(x+2)2﹣5
10.(2014 锦州)二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象如图,ax2+bx+c=m有实数根的条件是( )
A. m≥﹣2 B. m≥5 C. m≥0 D. m>4
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(10) (13) (14) (15)
11.(2014 凉山州)下列图形中阴影部分的面积相等的是( )
( http: / / www.21cnjy.com )
A. ②③ B. ③④ C. ①② D. ①④
12.(2014 台州)从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是( )
A.B.C.D.
13.(2013 安徽)如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是( )
A. 当弦PB最长时,△APC是等腰三角形 B. 当△APC是等腰三角形时,PO⊥AC
C. 当PO⊥AC时,∠ACP=30° D. 当∠ACP=30°时,△BPC是直角三角形
14.(2014 广安)如图,矩形ABC ( http: / / www.21cnjy.com )D的长为6,宽为3,点O1为矩形的中心,⊙O2的半径为1,O1O2⊥AB于点P,O1O2=6.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边只有一个公共点的情况一共出现( )
A. 3次 B. 4次 C. 5次 D. 6次
15.(2015 泰安模拟)如图,正方形ABCD的边AB=1,和都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
A. B. 1﹣ C. ﹣1 D. 1﹣
16.(2015 泰安模拟)如图,是一个工件的三视图,则此工件的全面积是( )
A. 60πcm2 B. 90πcm2 C. 96πcm2 D. 120πcm2
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(16) (19) (20)
17.(2014 石家庄一模)如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是( )
A. ①②③④ B. ④①③② C. ④②③① D. ④③②①
18.(2014 路南区三模)向上发射一枚 ( http: / / www.21cnjy.com )炮弹,经x秒后的高度为y公尺,且时间与高度关系为y=ax2+bx.若此炮弹在第7秒与第14秒时的高度相等,则在下列哪一个时间的高度是最高的( )
A. 第9.5秒 B. 第10秒 C. 第10.5秒 D. 第11秒
19.(2014 哈尔滨)如图,AB是⊙O ( http: / / www.21cnjy.com )的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是( )
A. 30° B. 25° C. 20° D. 15°
20.(2014 义乌市) ( http: / / www.21cnjy.com )一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A. 5:4 B. 5:2 C. :2 D. :
二.填空题(共5小题)
21.(2014 包头)如图,AB是⊙O的直径,BC是弦,点E是的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为 _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(21) (22)
22.画出几何体的俯视图、左视图.
23.(2014 攀枝花)在△ABC中,如果∠A、∠B满足|tanA﹣1|+(cosB﹣)2=0,那么∠C= .
24.(2014 牡丹江)抛物线y=ax2+bx+c经过点A(﹣3,0),对称轴是直线x=﹣1,则a+b+c= .
25.(2014 扬州)如图,抛物线y ( http: / / www.21cnjy.com )=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a﹣2b+c的值为 _________ .
三.解答题(共5小题)
26.(2014 丹东)在2014 ( http: / / www.21cnjy.com )年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x(x≥60)元,销售量为y套.
(1)求出y与x的函数关系式.
(2)当销售单价为多少元时,月销售额为14000元;
(3)当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少?
27.(2015 泰安模拟)甲、乙 ( http: / / www.21cnjy.com )两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.
( http: / / www.21cnjy.com )
28.(2014 泰安)二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
29.(2014 长沙)如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O的切线交AC于点E.
(1)求证:DE⊥AC;
(2)若AB=3DE,求tan∠ACB的值.
( http: / / www.21cnjy.com )
30.(2014 白银)如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
( http: / / www.21cnjy.com )
参考答案
一.选择题(共20小题)
1.D.2.A.3.D.4.B.5.C.6.B.7.D.8.D.9.A.10.A.
11.A.12.B.13.C.14.B.15.A.16.C.17.B.18.C.19.B.20.A.
填空题(共5小题)
8 .22. ( http: / / www.21cnjy.com )
23.75° .24. 0 25. 0 .
三.解答题(共5小题)
26.解:(1),∴y=﹣4x+480;
(2)根据题意可得,x(﹣4x+480)=14000,解得,x1=70,x2=50(不合题意舍去),
∴当销售价为70元时,月销售额为14000元.
(3)设一个月内获得的利润为w元,根据题意,得w=(x﹣40)(﹣4x+480),
=﹣4x2+640x﹣19200,=﹣4(x﹣80)2+6400,
当x=80时,w的最大值为6400
∴当销售单价为80元时,才能在一个月内获得最大利润,最大利润是6400元.
27.解:(1)作BD⊥AC于点D,如图所示:
由题意可知:AB=30×1=30海里,∠BAC=30°,∠BCA=45°,
在Rt△ABD中,
∵AB=30海里,∠BAC=30°,∴BD=15海里,AD=ABcos30°=15海里,
在Rt△BCD中,
∵BD=15海里,∠BCD=45°,∴CD=15海里,BC=15海里,
∴AC=AD+CD=15+15海里,
即A、C间的距离为(15+15)海里.
(2)∵AC=15+15(海里),轮船乙从A到C的时间为=+1,
由B到C的时间为+1﹣1=,
∵BC=15海里,∴轮船甲从B到C的速度为=5(海里/小时).
28.解:(1)由直线y=﹣x+1可知A(0,1),B(﹣3,),又点(﹣1,4)经过二次函数,
根据题意得: ( http: / / www.21cnjy.com ),解得:,则二次函数的解析式是:y=﹣﹣x+1;
(2)设N(x,﹣x2﹣x+1),则M(x,﹣x+1),P(x,0).∴MN=PN﹣PM
=﹣x2﹣x+1﹣(﹣x+1)=﹣x2﹣x=﹣(x+)2+,
则当x=﹣时,MN的最大值为;
(3)连接MN、BN、BM与NC互相垂直平分,即四边形BCMN是菱形,
由于BC∥MN,即MN=BC,且BC=MC,即﹣x2﹣x=,
且(﹣x+1)2+(x+3)2=,
解得:x=﹣1或x=﹣2(不合题意舍去),
故当N(﹣1,4)时,BM和NC互相垂直平分.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(27) (28) (29) (30)
29.(1)证明:连接OD,
∵D是BC的中点,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,
∵DE是⊙O的切线,∴OD⊥DE,∴DE⊥AC;
(2)解:连接AD,∵AB是⊙O的直径,∴∠ADB=90°,
∵DE⊥AC,∴∠ADC=∠DEC=∠AED=90°,∴∠ADE=∠DCE
在△ADE和△CDE中,∴△CDE∽△DAE,∴,
设tan∠ACB=x,CE=a,则DE=ax,AC=3ax,AE=3ax﹣a,
∴,整理得:x2﹣3x+1=0,解得:x=,∴tan∠ACB=.
30.(1)证明:连接OD,OE,∵AB为圆O的直径,∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,∴DE=BE,
在△OBE和△ODE中,,∴△OBE≌△ODE(SSS),∴∠ODE=∠ABC=90°,
则DE为圆O的切线;
(2)在Rt△ABC中,∠BAC=30°,∴BC=AC,∵BC=2DE=4,∴AC=8,
又∵∠C=60°,DE=CE,
∴△DEC为等边三角形,即DC=DE=2,则AD=AC﹣DC=6.
同课章节目录
