1.3 集合的基本运算(第一课时) 课件(15张PPT)
文档属性
| 名称 | 1.3 集合的基本运算(第一课时) 课件(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-21 09:03:11 | ||
图片预览






文档简介
(共15张PPT)
1.3 集合的基本运算
第一课时
人教A版2019必修第一册
学习目标
1. 理解交集与并集的概念,掌握交集与并集的区别与联系;
2. 会求两个已知集合的交集和并集,并能正确应用它们解决一些简单问题;
3. 能使用Venn图表达集合的运算,体会直观图示对理解抽象概念的作用.
问题1: 如何研究两个集合间的基本关系?
类比
实数
集合
问题2:实数可以进行加减乘除等运算,那么集合是否有类似的运算呢?
问题引入
新知讲解
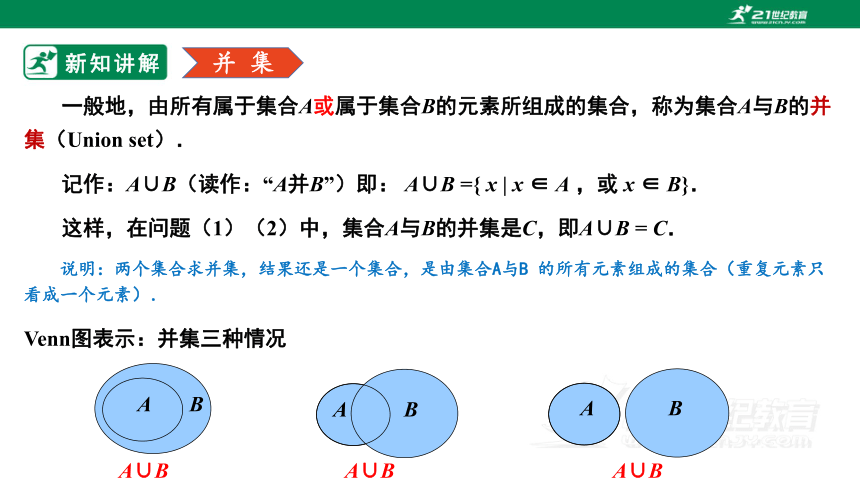
一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集(Union set).
记作:A∪B(读作:“A并B”)即: A∪B ={ x | x ∈ A ,或 x ∈ B}.
Venn图表示:并集三种情况
这样,在问题(1)(2)中,集合A与B的并集是C,即A∪B = C.
说明:两个集合求并集,结果还是一个集合,是由集合A与B 的所有元素组成的集合(重复元素只看成一个元素).
A∪B
A
B
A∪B
A
B
A∪B
A
B
并 集
典例分析
【例1】 设A={4,5,6,8},B={3,5,7,8},求A∪B.
【解析】A∪B={4,5,6,8} ∪ {3,5,7,8} ={3,4,5,6,7,8}.
A
4,6
B
3,7
5,8
求两个集合的并集时,它们的公共元素在并集中只能出现一次.
并 集
【例2】 设集合A={x|-1【解析】A∪B={x|-11
0
2
-1
3
A
B
注重数轴与韦恩图在解题中的应用:
①若给定的集合是不等式的解集,用数轴求解;
②若给定的集合是点集,用数形结合法求解;
③若给定的集合是抽象集合,用Venn图求解.
并 集
典例分析
思考探究
并集的性质
【性质①】A∪A=A 任何集合与其本身的并集都等于自身
【拓展】A,B,A∪B这三者的关系有如下5种情况:
【性质②】A∪ =A 任何集合与空集的并集都等于这个集合本身
A
B
A
B
B
B
A
A
A(B)
①A和B没有公共元素
②A和B有公共元素,
AA∪B,B A∪B
③B A,则
A∪B=A
④A B,则
A∪B=B
④A=B,则
A∪B=A=B
【注意】
(1)并集满足交换律和结合律
①A∪B=B∪A
②(A∪B)∪C=A∪(B∪C)
(2)常用结论:
①A(A∪B),B(A∪B)
②ABA∪B=B
一般地,由所有属于集合A且属于集合B的元素组成的集合,称为集合A与B的交集(intersection set).
记作:A∩B(读作:“A交B”) 即: A∩B ={ x | x ∈ A ,且 x ∈ B}.
这样,在上述问题(1)(2)中,集合A与B的交集是C,即A∩B = C.
A
B
A∩B=
A∩B=A
A
B
A
B
A∩B=C
C
Venn图表示:交集三种情况
交 集
新知讲解
典例分析
【例3】(1)已知集合A={x|-1≤x≤2},集合B={x|0≤x≤4},求A∩B.
(2)已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},求集合A∩B中元素的个数。
解:(1)在数轴上表示出集合A与B,如图:
则由交集的定义得,A∩B={x|0≤x≤2}.
交 集
(2)集合A中元素要满足x=3n+2,n∈N,即被3除余2,
而集合B中满足这一要求的元素
只有8和14,
所以集合A∩B中元素的个数为2.
思考探究
交集的性质
【拓展】A,B,A∩B这三者的关系有如下5种情况:
【性质②】A∩ = 任何集合与空集的交集都等于空集
A
B
A
B
B
B
A
A
A(B)
①A和B没有公共元素,
则A∩B=空
②A和B有公共元素,
AA,A∩B B
③B A,则
A∩B=B
④A B,则
A∩B=A
④A=B,则
A∩B=A=B
【注意】
(1)交集满足交换律和结合律
①A∩B=B∩A
②(A∩B)∩C=A∩(B∩C)
(2)常用结论:
①AA,A∩B B
②ABA∩B=A
【性质①】A∩A=A 任何集合与其本身的交集都等于自身
当堂检测
1、已知A={(x,y)|x+y= 3},B={(x,y)|x-y=1},则A∩B等于( )
(A){2,1} (B){x=2,y=1}
(C){(2,1)} (D)(2,1)
2、若集合A={x|-1答案:(1)C
解析:(2)借助数轴可知,
A∪B=R,A∩B={x|-1答案:(2)R {x|-13、A={x∈N|1≤x≤10},B={x∈R|x2+x-6=0},则图中阴影表示的集合为( )
(A){2} (B){3}
(C){-3,2} (D){-2,3}
4、设集合A={a,a2,0},B={2,4},若A∩B={2},则实数a的值为( )
(A)2 (B)±2
(C) (D)±
解析:(1)A={1,2,3,4,5,6,7,8,9,10},
B={-3,2},
又题图中阴影表示的集合是A∩B,
所以为{2}.故选A.
当堂检测
能力拓展
设集合M={x|-2为 .
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.3 集合的基本运算
第一课时
人教A版2019必修第一册
学习目标
1. 理解交集与并集的概念,掌握交集与并集的区别与联系;
2. 会求两个已知集合的交集和并集,并能正确应用它们解决一些简单问题;
3. 能使用Venn图表达集合的运算,体会直观图示对理解抽象概念的作用.
问题1: 如何研究两个集合间的基本关系?
类比
实数
集合
问题2:实数可以进行加减乘除等运算,那么集合是否有类似的运算呢?
问题引入
新知讲解
一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集(Union set).
记作:A∪B(读作:“A并B”)即: A∪B ={ x | x ∈ A ,或 x ∈ B}.
Venn图表示:并集三种情况
这样,在问题(1)(2)中,集合A与B的并集是C,即A∪B = C.
说明:两个集合求并集,结果还是一个集合,是由集合A与B 的所有元素组成的集合(重复元素只看成一个元素).
A∪B
A
B
A∪B
A
B
A∪B
A
B
并 集
典例分析
【例1】 设A={4,5,6,8},B={3,5,7,8},求A∪B.
【解析】A∪B={4,5,6,8} ∪ {3,5,7,8} ={3,4,5,6,7,8}.
A
4,6
B
3,7
5,8
求两个集合的并集时,它们的公共元素在并集中只能出现一次.
并 集
【例2】 设集合A={x|-1
0
2
-1
3
A
B
注重数轴与韦恩图在解题中的应用:
①若给定的集合是不等式的解集,用数轴求解;
②若给定的集合是点集,用数形结合法求解;
③若给定的集合是抽象集合,用Venn图求解.
并 集
典例分析
思考探究
并集的性质
【性质①】A∪A=A 任何集合与其本身的并集都等于自身
【拓展】A,B,A∪B这三者的关系有如下5种情况:
【性质②】A∪ =A 任何集合与空集的并集都等于这个集合本身
A
B
A
B
B
B
A
A
A(B)
①A和B没有公共元素
②A和B有公共元素,
AA∪B,B A∪B
③B A,则
A∪B=A
④A B,则
A∪B=B
④A=B,则
A∪B=A=B
【注意】
(1)并集满足交换律和结合律
①A∪B=B∪A
②(A∪B)∪C=A∪(B∪C)
(2)常用结论:
①A(A∪B),B(A∪B)
②ABA∪B=B
一般地,由所有属于集合A且属于集合B的元素组成的集合,称为集合A与B的交集(intersection set).
记作:A∩B(读作:“A交B”) 即: A∩B ={ x | x ∈ A ,且 x ∈ B}.
这样,在上述问题(1)(2)中,集合A与B的交集是C,即A∩B = C.
A
B
A∩B=
A∩B=A
A
B
A
B
A∩B=C
C
Venn图表示:交集三种情况
交 集
新知讲解
典例分析
【例3】(1)已知集合A={x|-1≤x≤2},集合B={x|0≤x≤4},求A∩B.
(2)已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},求集合A∩B中元素的个数。
解:(1)在数轴上表示出集合A与B,如图:
则由交集的定义得,A∩B={x|0≤x≤2}.
交 集
(2)集合A中元素要满足x=3n+2,n∈N,即被3除余2,
而集合B中满足这一要求的元素
只有8和14,
所以集合A∩B中元素的个数为2.
思考探究
交集的性质
【拓展】A,B,A∩B这三者的关系有如下5种情况:
【性质②】A∩ = 任何集合与空集的交集都等于空集
A
B
A
B
B
B
A
A
A(B)
①A和B没有公共元素,
则A∩B=空
②A和B有公共元素,
AA,A∩B B
③B A,则
A∩B=B
④A B,则
A∩B=A
④A=B,则
A∩B=A=B
【注意】
(1)交集满足交换律和结合律
①A∩B=B∩A
②(A∩B)∩C=A∩(B∩C)
(2)常用结论:
①AA,A∩B B
②ABA∩B=A
【性质①】A∩A=A 任何集合与其本身的交集都等于自身
当堂检测
1、已知A={(x,y)|x+y= 3},B={(x,y)|x-y=1},则A∩B等于( )
(A){2,1} (B){x=2,y=1}
(C){(2,1)} (D)(2,1)
2、若集合A={x|-1
解析:(2)借助数轴可知,
A∪B=R,A∩B={x|-1
(A){2} (B){3}
(C){-3,2} (D){-2,3}
4、设集合A={a,a2,0},B={2,4},若A∩B={2},则实数a的值为( )
(A)2 (B)±2
(C) (D)±
解析:(1)A={1,2,3,4,5,6,7,8,9,10},
B={-3,2},
又题图中阴影表示的集合是A∩B,
所以为{2}.故选A.
当堂检测
能力拓展
设集合M={x|-2
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
