1.4 充分条件与必要条件 课件(28张PPT)
文档属性
| 名称 | 1.4 充分条件与必要条件 课件(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-21 09:05:47 | ||
图片预览







文档简介
(共28张PPT)
1.4 充分条件与必要条件
人教A版2019必修第一册
学习目标
1、理解充分条件,必要条件的概念
2、通过对典型数学命题的梳理,理解充分条件与判定定理,必要条件与性质定理的关系
3、逻辑推理——能通过充分性、必要性解决简单的问题.
情境导入
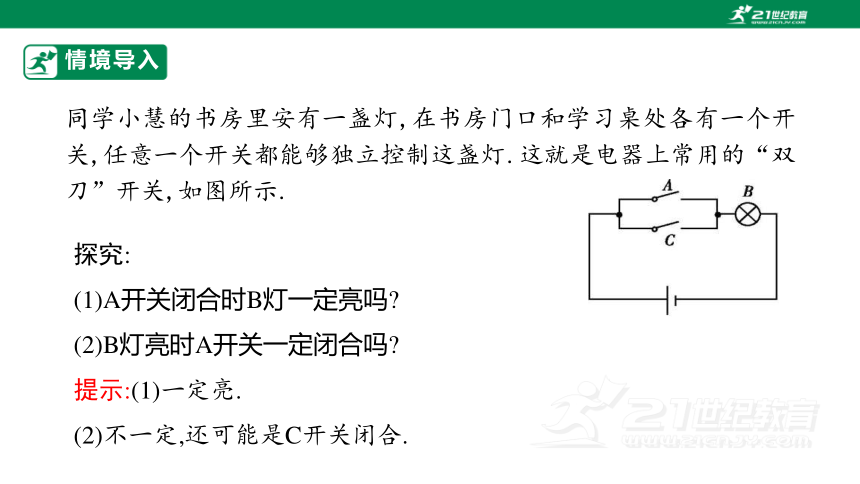
同学小慧的书房里安有一盏灯,在书房门口和学习桌处各有一个开关,任意一个开关都能够独立控制这盏灯.这就是电器上常用的“双刀”开关,如图所示.
探究:
(1)A开关闭合时B灯一定亮吗
(2)B灯亮时A开关一定闭合吗
提示:(1)一定亮.
(2)不一定,还可能是C开关闭合.
知识探究
判断下列命题的真假,并说明条件和结论具有怎样的逻辑关系
(1)若x>2,则x>1.
(2)若ab=0,则a=0.
(3)若平行四边形的对角线相等,则这个平行四边形是矩形.
提示:(1)为真命题,即条件“x>2”能够推出结论“x>1”.(2)为假命题,即条件“ab=0”推不出结论“a=0”.(3)为真命题,即条件“平行四边形的对角线相等”能够推出结论“这个平行四边形是矩形”.
新知讲解
一般地“若p,则q”为真命题,是指由p通过推理可以得出q.
这时,我们就说,由p可以推出q,记作 ,并且说,p是q的充分条件,q是p的必要条件.
如果“若p,则q”为假命题,那么由条件p不能推出结论q,记作p q.
此时,我们就说p不是q的充分条件,q不是p的必要条件.
/
上述命题(1) 、(4)中的p是q的充分条件,q是p的必要条件;命题(2) 、(3)中的p不是q的充分条件,q不是p的必要条件.
新知讲解
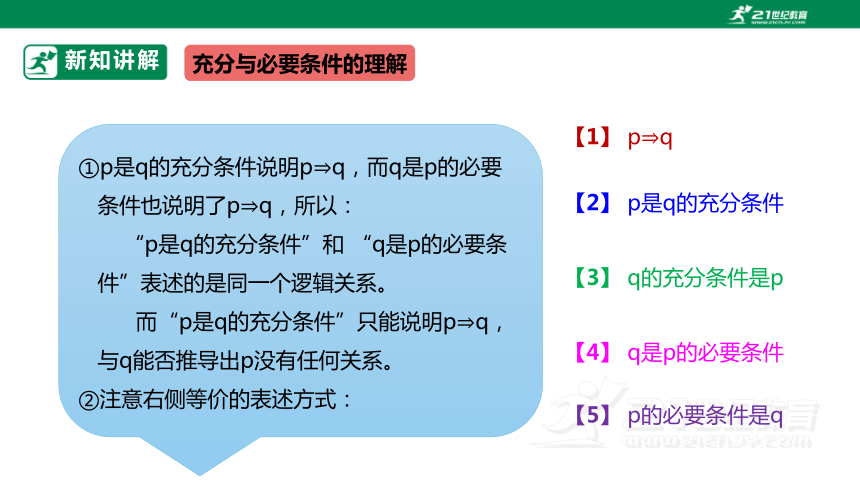
充分与必要条件的理解
①p是q的充分条件说明pq,而q是p的必要
条件也说明了pq,所以:
“p是q的充分条件”和 “q是p的必要条
件”表述的是同一个逻辑关系。
而“p是q的充分条件”只能说明pq,
与q能否推导出p没有任何关系。
②注意右侧等价的表述方式:
【1】 pq
【2】 p是q的充分条件
【3】 q的充分条件是p
【4】 q是p的必要条件
【5】 p的必要条件是q
典例分析
【例1】下列各组命题中,哪组命题中的p是q的充分条件(同时q是p的必要条件)
(-1)2 =1,显然-1≠1.
x=y= 时,显然xy=2,是有理数.
(1) p:四边形的两组对角分别相等;q:四边形是平行四边形;
(2) p:两个三角形的三边成比例;q:两个三角形相似;
(3) p:四边形为菱形;q:四边形的对角线互相垂直;
(4) p:x2 =1;q:x=1;
(5) p:a=b;q:ac=bc;
(6) p:x,y为无理数;q:xy为无理数.
×
√
√
√
×
√
典例分析
【例2】下列各组命题中,哪组命题中的p是q的必要条件(同时q是p的充分条件)?
√
(1) p:四边形的两组对角分别相等;q:四边形是平行四边形;
(2) p:两个三角形的三边成比例;q:两个三角形相似;
(3) p:四边形为菱形;q:四边形的对角线互相垂直;
(4) p:x2 =1;q:x=1;
(5) p:a=b;q:ac=bc;
(6) p:x,y为无理数;q:xy为无理数.
√
√
×
×
×
新知讲解
【逆命题】将命题“若p,则q”中的条件和结论互换,就得到一个新的命题:
“若q,则p”,这个就是原命题的逆命题。
【充要条件】
一般地,如果p可以推导出q,并且q也可以推导出p,即pq,且有
q p,则相当于pq或者q p,称作q是p的充分必要条件,q也是p的
充分必要条件,简称充要条件
【注意】充要条件是相互的,同时存在的, pq即p和q互为充要条件.
新知讲解
【注意】p是q的充要条件也可以说成:
pq,且qp
pq,且qp
pq,且qp
pq,且qp
p是q的充分不必要条件
p是q的必要不充分条件
p是q的充要条件
p是q的既不充分也不必要条件
①p和q是等价的
②p成立当且仅当q成立
③q成立当且仅当p成立
典例分析
【例3】判断下列各组命题中,那么p是q的什么条件?
①充分不必要条件 ②必要不充分条件 ③充要条件
(1)p:四边形是正方形,q:四边形的对角线互相垂直且平分;
(2)p:两个三角形相似,q:两个三角形三边成比例;
(3)p:xy>0,q:x>0,y>0;
(4)p:x=1是一元二次方程ax +bx+c=0的一个根,q:a+b+c=0(a≠0).
①
②
③
③
典例分析
【例4】已知p,q都是r的充分条件,s是r的必要条件,q是s的必要条件,那么:
①s是q的什么条件? ②r是q的什么条件? ③p是q的什么条件?
【解】利用图示,表示出p,q,s,r之间的关系如下:
①因为qr,rs,所以qs;又有sq,所以s是q的充要条件
②因为rs,sq,所以rq;又有qr,所以r是q的充要条件
③因为pr,rs,sq,所以pq;又有qp,所以p是q的充分不必要条件
新知讲解
“若我是福建人,则我是中国人.” 为真命题.
小范围 推出 大范围
即 p:“我是福建人” q: “我是中国人”
记 “福建人”为集合P, “中国人”为集合Q,则有
注:如果一个命题中的条件和结论是由一个变量的取值范围构成的,我们在判定充分或必要性的时候就可以看作对两个集合关系的判定设p对应集合P,q对应集合Q,若P Q,则p是q的充分条件,同时q是p的必要条件.
新知讲解
集合法判断充分必要性
列出集合A={|p()}和集合B={|q()} ,利用集合的包含关系来判断,如图:
A
B
A
B
B
B
A
A
A(B)
A B
p是q的充分不必要条件
B A
p是q的必要不充分条件
A=B
p是q的充要条件
AB且BA
p是q的既不充分也不必要条件
典例分析
(3)“x2 -x-6≤0”的一个充分不必要条件可以是 ( )
A.-2≤x≤3 B.x≤3 C.x≥-2 D.0≤x≤3
【例5】(1)“x=5”是“x2-4x-5=0”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
(2)设x∈R,则“2-x≥0”是“|x-1|≤1”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
B
A
D
(4)不等式x(x-2)<0成立的一个必要不充分条件是( )
A.x∈(0,2) B.x∈[-1,+∞) C.x∈(0,1) D.x∈(1,3)
B
能力拓展
1、设A={x|-1<x<3},B={x|-1<x<m+1,x∈R},若x∈B成立的一个充分不必要条件是x∈A,求实数m的取值范围.
答案: m>2
解析:因为A={x|-1<x<3},x∈B成立的一个充分不必要条件是x∈A,所以A B,所以m+1>3,即m>2.
能力拓展
2、已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0),若p是q的必要不充分条件,求实数m的取值范围.
【解析】∵p:-2≤x≤10,q:1-m≤x≤1+m(m>0),
记
解得:m≤3,
∴0<m≤3.
又m>0,
由p是q的必要不充分条件可得
B A,
典例分析
【例5】已知ab≠0,求证:a+b=1是a3+b3+ab-a2-b2=0的充要条件.
提示:从充分性、必要性两方面证明.
证明:
①充分性:因为a+b=1,所以b=1-a,
所以a3+b3+ab-a2-b2=a3+(1-a)3+a(1-a)-a2-(1-a)2
=a3+1-3a+3a2-a3+a-a2-a2-1+2a-a2=0,
即a3+b3+ab-a2-b2=0;
②必要性:因为a3+b3+ab-a2-b2=0, (a+b)(a2-ab+b2)-(a2-ab+b2)=0,
所以(a2-ab+b2)(a+b-1)=0,
因为ab≠0, 所以a、b均不为0, 所以a2-ab+b2≠0,
所以a+b-1=0, 即a+b=1.
综上可知,当ab≠0时,a+b=1是a3+b3+ab-a2-b2=0的充要条件
充分必要条件的证明
变式训练
已知x,y都是非零实数,且x>y,求证:的充要条件是xy>0.
当堂检测
解析:当B=90°或C=90°时不能推出AB2+AC2=BC2,因此选A.
1、在△ABC中,AB2+AC2=BC2是△ABC为直角三角形的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
A
当堂检测
2、已知p:x>1, q:x≥2,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:因为{x|x≥2} {x|x>1},所以p是q的必要不充分条件,故选B.
B
当堂检测
解析: a2+b2>0,则a,b不同时为零,且至少有一个不为零;a,b中至少有一个不为零,则a2+b2>0.选D.
3、a,b中至少有一个不为零的充要条件是( )
A.ab=0 B.ab>0
C.a2+b2=0 D.a2+b2>0
D
当堂检测
4、(多选题)对任意实数a,b,c,给出下列命题,其中是真命题的是( )
A.“a=b”是“ac=bc”的充分条件
B.“a+5是无理数”是“a是无理数”的必要条件
C.“a>b”是“a2>b2”的充分条件
D.“a<5”是“a<3”的必要条件
ABD
解析:当“a=b”时,“ac=bc”成立,故A是真命题;当“a是无理数”时,“a+5是无理数”成立,故B是真命题;当“a>b”时,“a2>b2”不一定成立,如当a=1,b=-2时,a2当堂检测
答案:充分 必要
当堂检测
答案:x>2 x>-2(答案不唯一)
当堂检测
7、设p:x>1,q:x>a,若p是q的充分不必要条件,求实数a的取值范围.
【解析】设A={x|x>1}, B={x|x>a}.
所以a<1.
所以A B,
因为p是q的充分不必要条件,
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.4 充分条件与必要条件
人教A版2019必修第一册
学习目标
1、理解充分条件,必要条件的概念
2、通过对典型数学命题的梳理,理解充分条件与判定定理,必要条件与性质定理的关系
3、逻辑推理——能通过充分性、必要性解决简单的问题.
情境导入
同学小慧的书房里安有一盏灯,在书房门口和学习桌处各有一个开关,任意一个开关都能够独立控制这盏灯.这就是电器上常用的“双刀”开关,如图所示.
探究:
(1)A开关闭合时B灯一定亮吗
(2)B灯亮时A开关一定闭合吗
提示:(1)一定亮.
(2)不一定,还可能是C开关闭合.
知识探究
判断下列命题的真假,并说明条件和结论具有怎样的逻辑关系
(1)若x>2,则x>1.
(2)若ab=0,则a=0.
(3)若平行四边形的对角线相等,则这个平行四边形是矩形.
提示:(1)为真命题,即条件“x>2”能够推出结论“x>1”.(2)为假命题,即条件“ab=0”推不出结论“a=0”.(3)为真命题,即条件“平行四边形的对角线相等”能够推出结论“这个平行四边形是矩形”.
新知讲解
一般地“若p,则q”为真命题,是指由p通过推理可以得出q.
这时,我们就说,由p可以推出q,记作 ,并且说,p是q的充分条件,q是p的必要条件.
如果“若p,则q”为假命题,那么由条件p不能推出结论q,记作p q.
此时,我们就说p不是q的充分条件,q不是p的必要条件.
/
上述命题(1) 、(4)中的p是q的充分条件,q是p的必要条件;命题(2) 、(3)中的p不是q的充分条件,q不是p的必要条件.
新知讲解
充分与必要条件的理解
①p是q的充分条件说明pq,而q是p的必要
条件也说明了pq,所以:
“p是q的充分条件”和 “q是p的必要条
件”表述的是同一个逻辑关系。
而“p是q的充分条件”只能说明pq,
与q能否推导出p没有任何关系。
②注意右侧等价的表述方式:
【1】 pq
【2】 p是q的充分条件
【3】 q的充分条件是p
【4】 q是p的必要条件
【5】 p的必要条件是q
典例分析
【例1】下列各组命题中,哪组命题中的p是q的充分条件(同时q是p的必要条件)
(-1)2 =1,显然-1≠1.
x=y= 时,显然xy=2,是有理数.
(1) p:四边形的两组对角分别相等;q:四边形是平行四边形;
(2) p:两个三角形的三边成比例;q:两个三角形相似;
(3) p:四边形为菱形;q:四边形的对角线互相垂直;
(4) p:x2 =1;q:x=1;
(5) p:a=b;q:ac=bc;
(6) p:x,y为无理数;q:xy为无理数.
×
√
√
√
×
√
典例分析
【例2】下列各组命题中,哪组命题中的p是q的必要条件(同时q是p的充分条件)?
√
(1) p:四边形的两组对角分别相等;q:四边形是平行四边形;
(2) p:两个三角形的三边成比例;q:两个三角形相似;
(3) p:四边形为菱形;q:四边形的对角线互相垂直;
(4) p:x2 =1;q:x=1;
(5) p:a=b;q:ac=bc;
(6) p:x,y为无理数;q:xy为无理数.
√
√
×
×
×
新知讲解
【逆命题】将命题“若p,则q”中的条件和结论互换,就得到一个新的命题:
“若q,则p”,这个就是原命题的逆命题。
【充要条件】
一般地,如果p可以推导出q,并且q也可以推导出p,即pq,且有
q p,则相当于pq或者q p,称作q是p的充分必要条件,q也是p的
充分必要条件,简称充要条件
【注意】充要条件是相互的,同时存在的, pq即p和q互为充要条件.
新知讲解
【注意】p是q的充要条件也可以说成:
pq,且qp
pq,且qp
pq,且qp
pq,且qp
p是q的充分不必要条件
p是q的必要不充分条件
p是q的充要条件
p是q的既不充分也不必要条件
①p和q是等价的
②p成立当且仅当q成立
③q成立当且仅当p成立
典例分析
【例3】判断下列各组命题中,那么p是q的什么条件?
①充分不必要条件 ②必要不充分条件 ③充要条件
(1)p:四边形是正方形,q:四边形的对角线互相垂直且平分;
(2)p:两个三角形相似,q:两个三角形三边成比例;
(3)p:xy>0,q:x>0,y>0;
(4)p:x=1是一元二次方程ax +bx+c=0的一个根,q:a+b+c=0(a≠0).
①
②
③
③
典例分析
【例4】已知p,q都是r的充分条件,s是r的必要条件,q是s的必要条件,那么:
①s是q的什么条件? ②r是q的什么条件? ③p是q的什么条件?
【解】利用图示,表示出p,q,s,r之间的关系如下:
①因为qr,rs,所以qs;又有sq,所以s是q的充要条件
②因为rs,sq,所以rq;又有qr,所以r是q的充要条件
③因为pr,rs,sq,所以pq;又有qp,所以p是q的充分不必要条件
新知讲解
“若我是福建人,则我是中国人.” 为真命题.
小范围 推出 大范围
即 p:“我是福建人” q: “我是中国人”
记 “福建人”为集合P, “中国人”为集合Q,则有
注:如果一个命题中的条件和结论是由一个变量的取值范围构成的,我们在判定充分或必要性的时候就可以看作对两个集合关系的判定设p对应集合P,q对应集合Q,若P Q,则p是q的充分条件,同时q是p的必要条件.
新知讲解
集合法判断充分必要性
列出集合A={|p()}和集合B={|q()} ,利用集合的包含关系来判断,如图:
A
B
A
B
B
B
A
A
A(B)
A B
p是q的充分不必要条件
B A
p是q的必要不充分条件
A=B
p是q的充要条件
AB且BA
p是q的既不充分也不必要条件
典例分析
(3)“x2 -x-6≤0”的一个充分不必要条件可以是 ( )
A.-2≤x≤3 B.x≤3 C.x≥-2 D.0≤x≤3
【例5】(1)“x=5”是“x2-4x-5=0”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
(2)设x∈R,则“2-x≥0”是“|x-1|≤1”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
B
A
D
(4)不等式x(x-2)<0成立的一个必要不充分条件是( )
A.x∈(0,2) B.x∈[-1,+∞) C.x∈(0,1) D.x∈(1,3)
B
能力拓展
1、设A={x|-1<x<3},B={x|-1<x<m+1,x∈R},若x∈B成立的一个充分不必要条件是x∈A,求实数m的取值范围.
答案: m>2
解析:因为A={x|-1<x<3},x∈B成立的一个充分不必要条件是x∈A,所以A B,所以m+1>3,即m>2.
能力拓展
2、已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0),若p是q的必要不充分条件,求实数m的取值范围.
【解析】∵p:-2≤x≤10,q:1-m≤x≤1+m(m>0),
记
解得:m≤3,
∴0<m≤3.
又m>0,
由p是q的必要不充分条件可得
B A,
典例分析
【例5】已知ab≠0,求证:a+b=1是a3+b3+ab-a2-b2=0的充要条件.
提示:从充分性、必要性两方面证明.
证明:
①充分性:因为a+b=1,所以b=1-a,
所以a3+b3+ab-a2-b2=a3+(1-a)3+a(1-a)-a2-(1-a)2
=a3+1-3a+3a2-a3+a-a2-a2-1+2a-a2=0,
即a3+b3+ab-a2-b2=0;
②必要性:因为a3+b3+ab-a2-b2=0, (a+b)(a2-ab+b2)-(a2-ab+b2)=0,
所以(a2-ab+b2)(a+b-1)=0,
因为ab≠0, 所以a、b均不为0, 所以a2-ab+b2≠0,
所以a+b-1=0, 即a+b=1.
综上可知,当ab≠0时,a+b=1是a3+b3+ab-a2-b2=0的充要条件
充分必要条件的证明
变式训练
已知x,y都是非零实数,且x>y,求证:的充要条件是xy>0.
当堂检测
解析:当B=90°或C=90°时不能推出AB2+AC2=BC2,因此选A.
1、在△ABC中,AB2+AC2=BC2是△ABC为直角三角形的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
A
当堂检测
2、已知p:x>1, q:x≥2,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:因为{x|x≥2} {x|x>1},所以p是q的必要不充分条件,故选B.
B
当堂检测
解析: a2+b2>0,则a,b不同时为零,且至少有一个不为零;a,b中至少有一个不为零,则a2+b2>0.选D.
3、a,b中至少有一个不为零的充要条件是( )
A.ab=0 B.ab>0
C.a2+b2=0 D.a2+b2>0
D
当堂检测
4、(多选题)对任意实数a,b,c,给出下列命题,其中是真命题的是( )
A.“a=b”是“ac=bc”的充分条件
B.“a+5是无理数”是“a是无理数”的必要条件
C.“a>b”是“a2>b2”的充分条件
D.“a<5”是“a<3”的必要条件
ABD
解析:当“a=b”时,“ac=bc”成立,故A是真命题;当“a是无理数”时,“a+5是无理数”成立,故B是真命题;当“a>b”时,“a2>b2”不一定成立,如当a=1,b=-2时,a2
答案:充分 必要
当堂检测
答案:x>2 x>-2(答案不唯一)
当堂检测
7、设p:x>1,q:x>a,若p是q的充分不必要条件,求实数a的取值范围.
【解析】设A={x|x>1}, B={x|x>a}.
所以a<1.
所以A B,
因为p是q的充分不必要条件,
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
