11.2.1 三角形的内角 学案 2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 11.2.1 三角形的内角 学案 2023—2024学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 47.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-21 12:30:32 | ||
图片预览

文档简介
第十一章 三角形
11.2.1 三角形的内角
第1课时 三角形的内角和 学习任务单
【学习目标】
1.会用平行线的性质与平角的定义证明三角形内角和等于180°.
2.会运用三角形内角和定理进行计算.
【学习任务】
1.三角形的内角和定理的证明;
2.三角形的内角和定理也常常用在实际问题中.
【学习探究】
任务一:三角形的内角和定理的证明
活动1:自学教材P页完成《学习任务单》的活动1、2(3分钟).
三角形三个内角的和等于180°.
已知:△ABC.
求证:∠A+∠B+∠C=180°
证法1: 证法2: 证法3:
思考:多种方法证明三角形内角和等于180°的核心是什么?
归纳小结:
活动2:如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
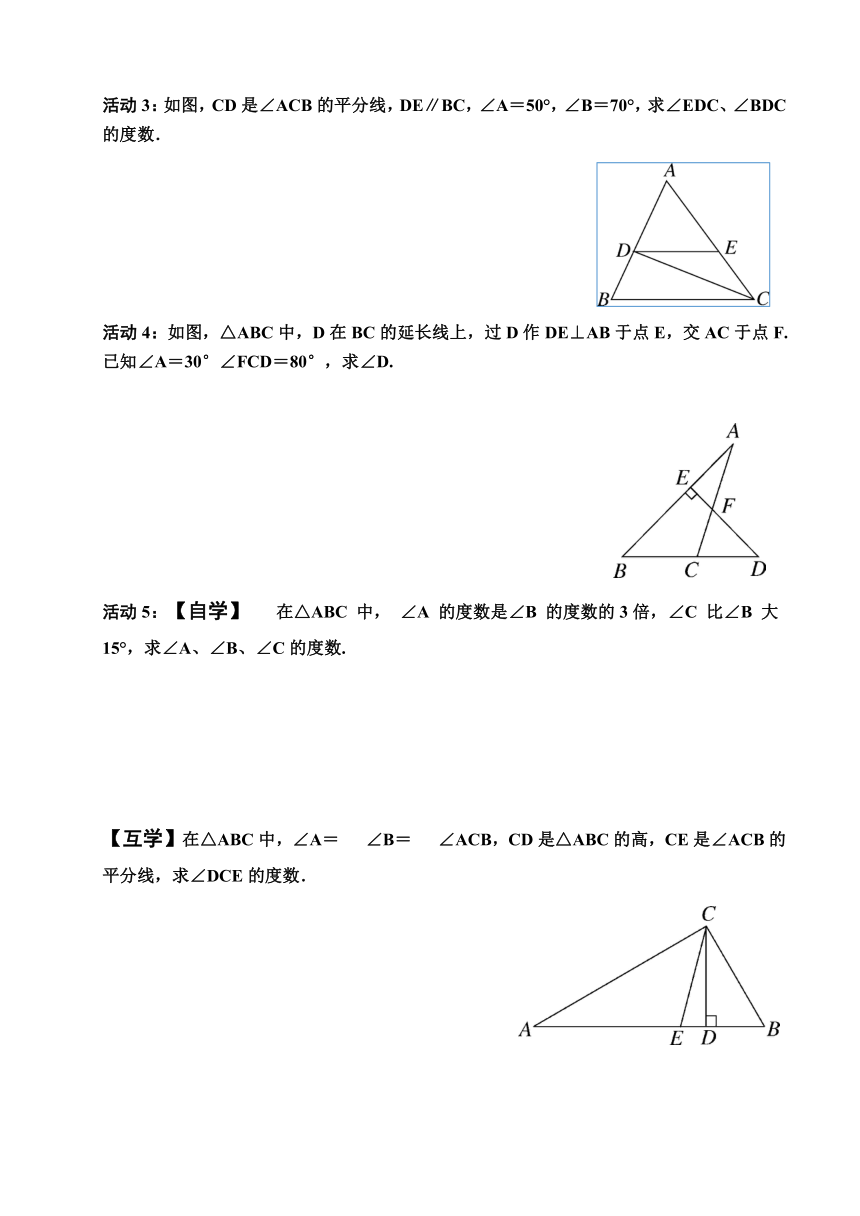
活动3:如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC、∠BDC的度数.
活动4:如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于点E,交AC于点F.已知∠A=30°∠FCD=80°,求∠D.
活动5:【自学】 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A、∠B、∠C的度数.
【互学】在△ABC中,∠A= ∠B= ∠ACB,CD是△ABC的高,CE是∠ACB的平分线,求∠DCE的度数.
任务二:三角形的内角和定理也常常用在实际问题中
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向.从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
【互学】如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A/B两岛的视角∠ACB的度数.
活动6:如图,四边形ABCD中,点E在B上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
【学习反思】
1.我的收获:
;
2.我的疑问:
.
【学习评价】
1.如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,若∠BAC=60°,求∠BPC的度数.
2.如图,AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC平分∠ABP交AM于点C,BD平分∠PBN交AM于点D.
(1)求∠ABN的度数.
(2)求∠CBD的度数.
11.2.1 三角形的内角
第1课时 三角形的内角和 学习任务单
【学习目标】
1.会用平行线的性质与平角的定义证明三角形内角和等于180°.
2.会运用三角形内角和定理进行计算.
【学习任务】
1.三角形的内角和定理的证明;
2.三角形的内角和定理也常常用在实际问题中.
【学习探究】
任务一:三角形的内角和定理的证明
活动1:自学教材P页完成《学习任务单》的活动1、2(3分钟).
三角形三个内角的和等于180°.
已知:△ABC.
求证:∠A+∠B+∠C=180°
证法1: 证法2: 证法3:
思考:多种方法证明三角形内角和等于180°的核心是什么?
归纳小结:
活动2:如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
活动3:如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC、∠BDC的度数.
活动4:如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于点E,交AC于点F.已知∠A=30°∠FCD=80°,求∠D.
活动5:【自学】 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A、∠B、∠C的度数.
【互学】在△ABC中,∠A= ∠B= ∠ACB,CD是△ABC的高,CE是∠ACB的平分线,求∠DCE的度数.
任务二:三角形的内角和定理也常常用在实际问题中
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向.从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
【互学】如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A/B两岛的视角∠ACB的度数.
活动6:如图,四边形ABCD中,点E在B上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
【学习反思】
1.我的收获:
;
2.我的疑问:
.
【学习评价】
1.如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,若∠BAC=60°,求∠BPC的度数.
2.如图,AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC平分∠ABP交AM于点C,BD平分∠PBN交AM于点D.
(1)求∠ABN的度数.
(2)求∠CBD的度数.
