第21章 二次函数与反比例函数 章末测试题(含答案)2023-2024学年沪科版数学九年级上册
文档属性
| 名称 | 第21章 二次函数与反比例函数 章末测试题(含答案)2023-2024学年沪科版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 396.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-21 12:38:34 | ||
图片预览



文档简介
第21章《二次函数与反比例函数》章末测试题
2023-2024学年九年级上册数学沪科版
一、单选题(本大题共12小题,每小题3分,共36分)
1.若二次函数与x轴的一个交点为,则代数式的值为( )
A. B. C. D.
2.为做好校园防疫工作,每日会对教室进行药物喷洒消毒,药物喷洒完成后,消毒药物在教室内空气中的浓度和时间满足关系(),已知测得当时,药物浓度,则的值为( )
A.50 B. C.5 D.15
3.设,,是抛物线上的三点,则,,的大小关系为
A. B.
C. D.
4.如图,点,点都在反比例函数的图象上,过点分别向轴、轴作垂线,垂足分别为点,.连接,,.若四边形的面积记作,的面积记作,则( )
A. B. C. D.
5.点在反比例函数的图像上,当时,y的取值范围是( )
A. B. C. D.
6.已知点与点在反比例函数的图象上,( )
A.若,则 B.若,则
C.若,则 D.若,则
7.如图,一次函数与反比例函数的图象交点A(m,4)和B(-8,-2)两点,若y1>y2,则x的取值范围是( )
A.或
B.或
C.
D.或
8.如图,小聪要在抛物线y =x(2-x)上找一点M(a,b),针对b的不同取值,所找点M的个数,三个同学的说法如下,
小明:若b=-3,则点M的个数为0;
小云:若b = 1,则点M的个数为1;
小朵:若b = 3,则点M的个数为2.
下列判断正确的是( ).
A.小云错,小朵对 B.小明,小云都错 C.小云对,小朵错 D.小明错,小朵对
9.老师给出了二次函数的部分对应值如下表,同学们讨论得出了下列结论,其中不正确的是( )
x … -3 -2 0 1 3 5 …
y … 7 0 -8 -9 -5 7 …
A.抛物线的对称轴为直线
B.是方程的一个根
C.若,是该抛物线上的两点,则
D.当时,
10.在平面直角坐标系xOy中,若函数的函数值y随着自变量x的增大而增大,则函数的图象所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.关于二次函数y=-(x -2)2+3,以下说法正确的是( )
A.当x>-2时,y随x增大而减小 B.当x>-2时,y随x增大而增大
C.当x>2时,y随x增大而减小 D.当x>2时,y随x增大而增大
12.如图,在平面直角坐标系中,为正方形的对称中心,,分别在轴和轴上,双曲线经过、两点,则正方形的边长为( )
A. B.3 C. D.4
二、填空题(本大题共8小题,每小题3分,共24分)
13.已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有 .
14.已知,二次函数,当时,则y的取值范围是 .
15.如图,抛物线与x轴交于A、B两点,P是以点为圆心,1为半径的圆上的动点,Q是线段的中点,连接.则线段的最大值是 .
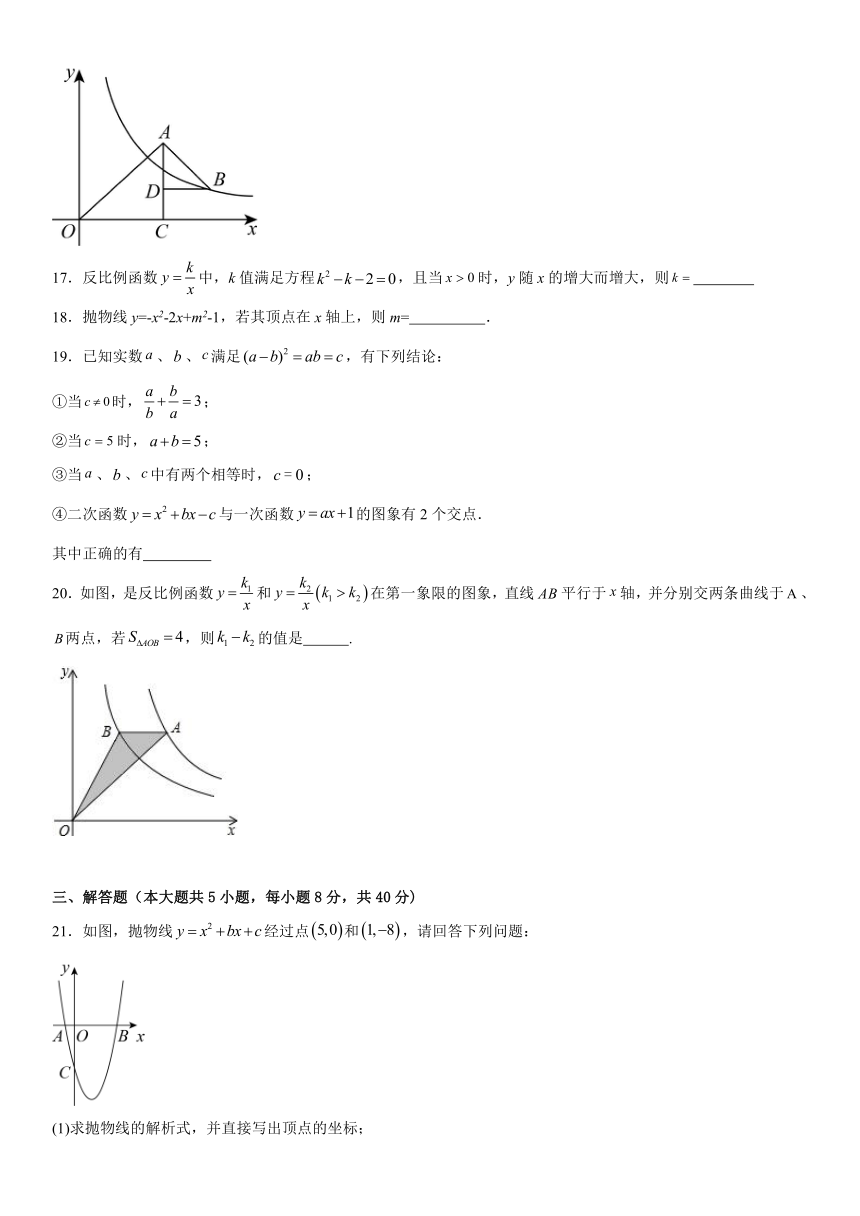
16.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则OA2﹣AB2= .
17.反比例函数中,k值满足方程,且当时,y随x的增大而增大,则
18.抛物线y=-x2-2x+m2-1,若其顶点在x轴上,则m= .
19.已知实数、、满足,有下列结论:
①当时,;
②当时,;
③当、、中有两个相等时,;
④二次函数与一次函数的图象有2个交点.
其中正确的有
20.如图,是反比例函数和在第一象限的图象,直线平行于轴,并分别交两条曲线于、两点,若,则的值是 .
三、解答题(本大题共5小题,每小题8分,共40分)
21.如图,抛物线经过点和,请回答下列问题:
(1)求抛物线的解析式,并直接写出顶点的坐标;
(2)若抛物线与轴交于、两点,与轴交于点,连接、,求的面积;
(3)在抛物线上是否存在一点(点不与点重合)使,若存在,请直接写出点的坐标:若不存在,说明理由.
22.在平面直角坐标系xOy中,O为坐标原点,一次函数的图像与反比例函数的图像交于点A(1,),交x轴于点B.
(1)求k的值;
(2)求△AOB的面积.
23.某超市销售一种饮料, 每瓶进价为元,当每瓶售价元时,日均销售量瓶.经市场调查表明,每瓶售价每增加元,日均销售量减少瓶.
(1)当每瓶售价为元时,日均销售量为 瓶;
(2)当每瓶售价为多少元时,所得日均总利润为元;
(3)当每瓶售价为多少元时,所得日均总利润最大?最大日均总利润为多少元?
24.如图,抛物线过点,,与轴交于点.
(1)求该抛物线的解析式;
(2)如图1,直线的解析式为,抛物线的对称轴与线段交于点,过点作直线的垂线,垂足为点,连接,求的面积;
(3)图1中的直线向下平移4个单位长度得到直线如图2,直线与轴交于点.点是折线上的一点,过点分别作轴、直线的垂线,垂足为点,是否存点,使得以为顶点的三角形是等腰三角形.若存在,直接写出点的坐标;若不存在,请说明理由.
25.媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所
示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?
参考答案:
1.A
2.A
3.A
4.C
5.A
6.D
7.B
8.C
9.C
10.B
11.C
12.C
13.③④
14.
15.3
16.12
17.
18.
19.①④
20.8
21.(1),顶点坐标为
(2)
(3)存在,点P的坐标为或或
22.(1)k =1 (2)
23.(1);(2)元或元;(3)元时利润最大,最大利润元
24.(1);(2)8;(3)存在满足条件的点,点坐标为:、、、.
25.(1)y=(x≥15),(2)从消毒开始,师生至少在75分钟内不能进入教室.
2023-2024学年九年级上册数学沪科版
一、单选题(本大题共12小题,每小题3分,共36分)
1.若二次函数与x轴的一个交点为,则代数式的值为( )
A. B. C. D.
2.为做好校园防疫工作,每日会对教室进行药物喷洒消毒,药物喷洒完成后,消毒药物在教室内空气中的浓度和时间满足关系(),已知测得当时,药物浓度,则的值为( )
A.50 B. C.5 D.15
3.设,,是抛物线上的三点,则,,的大小关系为
A. B.
C. D.
4.如图,点,点都在反比例函数的图象上,过点分别向轴、轴作垂线,垂足分别为点,.连接,,.若四边形的面积记作,的面积记作,则( )
A. B. C. D.
5.点在反比例函数的图像上,当时,y的取值范围是( )
A. B. C. D.
6.已知点与点在反比例函数的图象上,( )
A.若,则 B.若,则
C.若,则 D.若,则
7.如图,一次函数与反比例函数的图象交点A(m,4)和B(-8,-2)两点,若y1>y2,则x的取值范围是( )
A.或
B.或
C.
D.或
8.如图,小聪要在抛物线y =x(2-x)上找一点M(a,b),针对b的不同取值,所找点M的个数,三个同学的说法如下,
小明:若b=-3,则点M的个数为0;
小云:若b = 1,则点M的个数为1;
小朵:若b = 3,则点M的个数为2.
下列判断正确的是( ).
A.小云错,小朵对 B.小明,小云都错 C.小云对,小朵错 D.小明错,小朵对
9.老师给出了二次函数的部分对应值如下表,同学们讨论得出了下列结论,其中不正确的是( )
x … -3 -2 0 1 3 5 …
y … 7 0 -8 -9 -5 7 …
A.抛物线的对称轴为直线
B.是方程的一个根
C.若,是该抛物线上的两点,则
D.当时,
10.在平面直角坐标系xOy中,若函数的函数值y随着自变量x的增大而增大,则函数的图象所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.关于二次函数y=-(x -2)2+3,以下说法正确的是( )
A.当x>-2时,y随x增大而减小 B.当x>-2时,y随x增大而增大
C.当x>2时,y随x增大而减小 D.当x>2时,y随x增大而增大
12.如图,在平面直角坐标系中,为正方形的对称中心,,分别在轴和轴上,双曲线经过、两点,则正方形的边长为( )
A. B.3 C. D.4
二、填空题(本大题共8小题,每小题3分,共24分)
13.已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有 .
14.已知,二次函数,当时,则y的取值范围是 .
15.如图,抛物线与x轴交于A、B两点,P是以点为圆心,1为半径的圆上的动点,Q是线段的中点,连接.则线段的最大值是 .
16.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则OA2﹣AB2= .
17.反比例函数中,k值满足方程,且当时,y随x的增大而增大,则
18.抛物线y=-x2-2x+m2-1,若其顶点在x轴上,则m= .
19.已知实数、、满足,有下列结论:
①当时,;
②当时,;
③当、、中有两个相等时,;
④二次函数与一次函数的图象有2个交点.
其中正确的有
20.如图,是反比例函数和在第一象限的图象,直线平行于轴,并分别交两条曲线于、两点,若,则的值是 .
三、解答题(本大题共5小题,每小题8分,共40分)
21.如图,抛物线经过点和,请回答下列问题:
(1)求抛物线的解析式,并直接写出顶点的坐标;
(2)若抛物线与轴交于、两点,与轴交于点,连接、,求的面积;
(3)在抛物线上是否存在一点(点不与点重合)使,若存在,请直接写出点的坐标:若不存在,说明理由.
22.在平面直角坐标系xOy中,O为坐标原点,一次函数的图像与反比例函数的图像交于点A(1,),交x轴于点B.
(1)求k的值;
(2)求△AOB的面积.
23.某超市销售一种饮料, 每瓶进价为元,当每瓶售价元时,日均销售量瓶.经市场调查表明,每瓶售价每增加元,日均销售量减少瓶.
(1)当每瓶售价为元时,日均销售量为 瓶;
(2)当每瓶售价为多少元时,所得日均总利润为元;
(3)当每瓶售价为多少元时,所得日均总利润最大?最大日均总利润为多少元?
24.如图,抛物线过点,,与轴交于点.
(1)求该抛物线的解析式;
(2)如图1,直线的解析式为,抛物线的对称轴与线段交于点,过点作直线的垂线,垂足为点,连接,求的面积;
(3)图1中的直线向下平移4个单位长度得到直线如图2,直线与轴交于点.点是折线上的一点,过点分别作轴、直线的垂线,垂足为点,是否存点,使得以为顶点的三角形是等腰三角形.若存在,直接写出点的坐标;若不存在,请说明理由.
25.媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所
示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?
参考答案:
1.A
2.A
3.A
4.C
5.A
6.D
7.B
8.C
9.C
10.B
11.C
12.C
13.③④
14.
15.3
16.12
17.
18.
19.①④
20.8
21.(1),顶点坐标为
(2)
(3)存在,点P的坐标为或或
22.(1)k =1 (2)
23.(1);(2)元或元;(3)元时利润最大,最大利润元
24.(1);(2)8;(3)存在满足条件的点,点坐标为:、、、.
25.(1)y=(x≥15),(2)从消毒开始,师生至少在75分钟内不能进入教室.
