21.2.1 配方法的应用同步练习 (含答案)
文档属性
| 名称 | 21.2.1 配方法的应用同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-20 17:23:00 | ||
图片预览



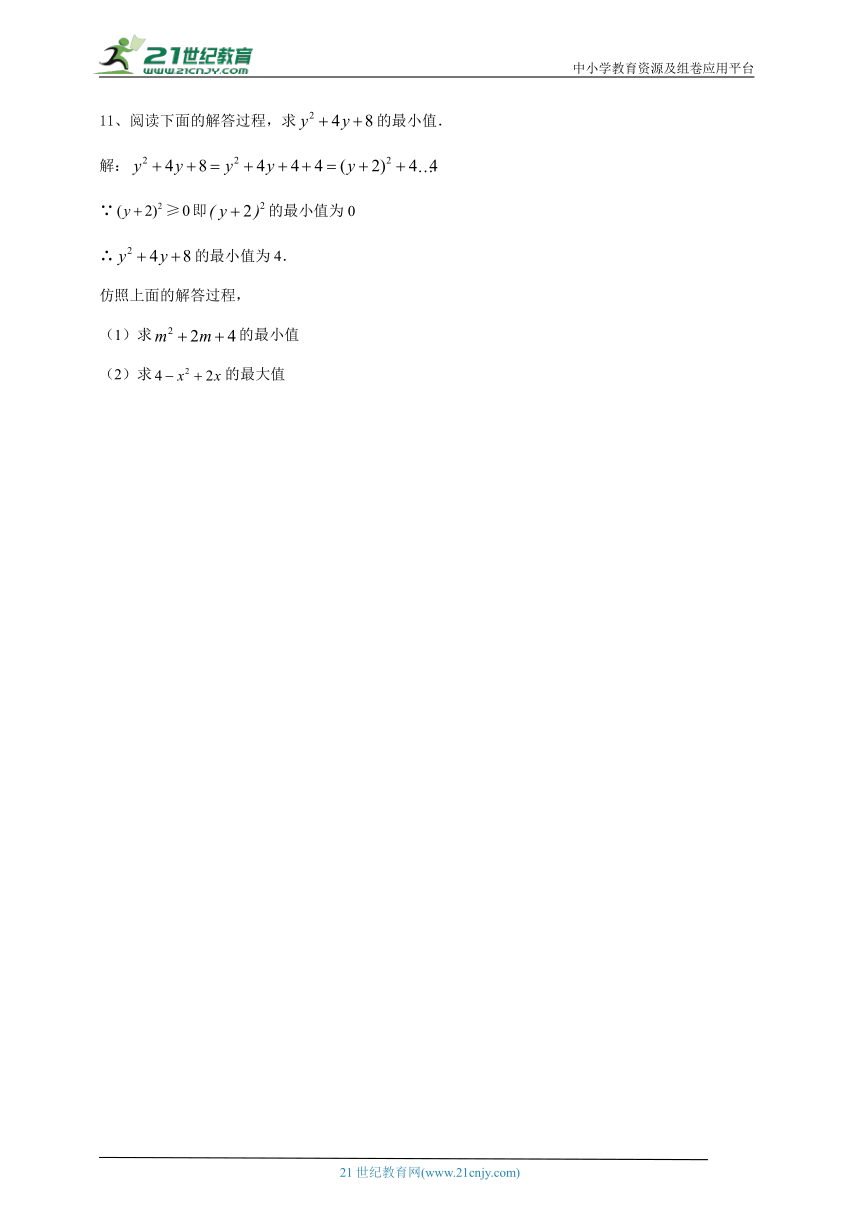

文档简介
中小学教育资源及组卷应用平台
专题3 配方法解一元二次方程配方法的应用
1、用配方法解方程,变形后的结果正确的是( )
A. B. C. D.
2、已知方程x2﹣6x﹣2=0,用配方法化为a(x+b)2=c的形式为_____.
3、若把代数式化为的形式,其中、为常数,则______.
4、已知实数a、b、c,满足a2﹣a+b=0,c=4a2﹣4a+b2﹣,则实数c的取值范围是____.
5、用适当的方法解下列方程.
(1); (2).
6、阅读理解:已知,求m 、n的值.
解:∵
∴
∴
∴
∴.
方法应用:(1)已知,求a 、b 的值;
(2)已知 .
①用含 y 的式子表示 x : ;
②若,求 的值.
7、特值验证:
当,0,1,2,5,…时,计算代数式的值,分别得到5,2,1,2,17,….当x的取值发生变化时,代数式的值却有一个确定的范围,通过多次验证可以发现它的值总大于或等于1,所以1就是它的最小值.
变式求证:我们可以用学过的知识,对进行恒等变形:.(注:这种变形方法可称为“配方”) ,.所以无论x取何值,代数式的值不小于1,即最小值为1.
迁移实证:(1)请你用“配方”的方法,确定的最小值为3;
(2)求的最大值.
8、阅读材料:把形如的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即.例如:是的一种形式的配方;所以,,,是的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).请根据阅读材料解决下列问题:
(1)比照上面的例子,写出三种不同形式的配方;
(2)已知,求的值;
(3)已知,求的值.
9、先阅读下面的内容,再解决问题:
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
∵m2+2mn+2n2﹣6n+9=0∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0∴m+n=0,n﹣3=0∴m=﹣3,n=3
根据你的观察,探究下面的问题:
(1)若x2+4x+4+y2﹣8y+16=0,求的值.
(2)试说明不论x,y取什么有理数时,多项式x2+y2﹣2x+2y+3的值总是正数.
(3)已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c比a、b都大,求c的取值范围.
10、若a,b,c为的三边.
(1)化简:|a﹣b+c|+|c﹣a﹣b|﹣|a+b|;
(2)若a,b,c都是正整数,且a2+b2﹣2a﹣8b+17=0,的周长.
11、阅读下面的解答过程,求的最小值.
解:
∵即的最小值为0
∴的最小值为4.
仿照上面的解答过程,
(1)求的最小值
(2)求的最大值
答案版
1、用配方法解方程,变形后的结果正确的是( )
A. B. C. D.
【解析】,
,
,
所以,
故选D.
2、已知方程x2﹣6x﹣2=0,用配方法化为a(x+b)2=c的形式为_____.
【答案】(x﹣3)2=11
【解析】方程x2﹣6x﹣2=0,
移项得:x2﹣6x=2,
配方得:x2﹣6x+9=11,即(x﹣3)2=11.
故答案为:(x﹣3)2=11.
3、若把代数式化为的形式,其中、为常数,则______.
【答案】-7
【解析】x 4x 5=x 4x+4 4 5
=(x 2) 9,
所以m=2,k= 9,
所以m+k=2 9= 7.
故答案为:-7
4、已知实数a、b、c,满足a2﹣a+b=0,c=4a2﹣4a+b2﹣,则实数c的取值范围是____.
【解析】∵a2﹣a+b=0,
∴a2﹣a=﹣b.
∴c=4a2﹣4a+b2﹣=4(a2﹣a)+b2﹣=﹣2b+b2﹣=(b﹣1)2﹣
∵(b﹣1)2≥0,
∴(b﹣1)2﹣≥﹣,即c≥﹣.
5、用适当的方法解下列方程.
(1);
(2).
【解析】(1),
,
,
,
,
所以;
(2)
二次项系数化为1得, ,
移项,得 ,
配方,得 ,
,
6、阅读理解:已知,求m 、n的值.
解:∵
∴
∴
∴
∴.
方法应用:(1)已知,求a 、b 的值;
(2)已知 .
①用含 y 的式子表示 x : ;
②若,求 的值.
【解析】(1)∵a2+b2-10a+4b+29=0,∴(a2-10a+25)+(b2+4b+4)=0,
∴(a-5)2+(b+2)2=0,
∴(a-5)2=0,(b+2)2=0,∴a=5,b=-2;
(2)①∵x+4y=4,
∴x=4-4y;
②∵xy-z2-6z=10,
∴y(4-4y)-z2-6z=10,
∴4y-4y2-z2-6z=10,
∴4y2-4y+z2+6z+10=0,
∴(2y-1)2+(z+3)2=0,
∴y=,z=-3,∴x=2,
∴yx+z的值=()2 3=2.
7、特值验证:
当,0,1,2,5,…时,计算代数式的值,分别得到5,2,1,2,17,….当x的取值发生变化时,代数式的值却有一个确定的范围,通过多次验证可以发现它的值总大于或等于1,所以1就是它的最小值.
变式求证:我们可以用学过的知识,对进行恒等变形:.(注:这种变形方法可称为“配方”) ,.所以无论x取何值,代数式的值不小于1,即最小值为1.
迁移实证:(1)请你用“配方”的方法,确定的最小值为3;
(2)求的最大值.
【解析】(1)证明:
,.所以得最小值为3.
(2)
, ,所以的最大值为.
8、阅读材料:把形如的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即.例如:是的一种形式的配方;所以,,,是的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).请根据阅读材料解决下列问题:
(1)比照上面的例子,写出三种不同形式的配方;
(2)已知,求的值;
(3)已知,求的值.
【解析】(1)的三种配方分别为:
;
;
(或;
(2)∵x2+y2-6x+10y+34=x2-6x+9+y2+10y+25=(x-3)2+(y+5)2=0,
∴x-3=0,y+5=0,
∴x=3,y=-5,
∴3x-2y=3×3-2×(-5)=19
(3)
∴,,
∴,,,
则
9、先阅读下面的内容,再解决问题:
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
∵m2+2mn+2n2﹣6n+9=0∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0∴m+n=0,n﹣3=0∴m=﹣3,n=3
根据你的观察,探究下面的问题:
(1)若x2+4x+4+y2﹣8y+16=0,求的值.
(2)试说明不论x,y取什么有理数时,多项式x2+y2﹣2x+2y+3的值总是正数.
(3)已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c比a、b都大,求c的取值范围.
【解析】(1)已知等式整理得:(x+2)2+(y﹣4)2=0,
可得x+2=0,y﹣4=0,
解得:x=﹣2,y=4,
则;
(2)∵(x﹣1)2≥0,(y+1)2≥0,
∴原式=(x﹣1)2+(y+1)2+1≥1,
则不论x,y取什么有理数时,多项式x2+y2﹣2x+2y+3的值总是正数;
(3)已知等式整理得:(a﹣5)2+(b﹣4)2=0,
可得a﹣5=0,b﹣4=0,
解得:a=5,b=4,
∵
则c的范围是5<c<9.
10、若a,b,c为的三边.
(1)化简:|a﹣b+c|+|c﹣a﹣b|﹣|a+b|;
(2)若a,b,c都是正整数,且a2+b2﹣2a﹣8b+17=0,的周长.
【解析】(1)∵a,b,c为△ABC的三边,
∴a﹣b+c>0,c﹣a﹣b<0,a+b>0,
∴|a﹣b+c|+|c﹣a﹣b|﹣|a+b|=a﹣b+c﹣c+a+b﹣a﹣b=a﹣b;
(2)∵a2+b2﹣2a﹣8b+17=(a2﹣2a+1)+(b2﹣8b+16)=(a﹣1)2+(b﹣4)2=0,∴a=1,b=4,
∵a,b,c为△ABC的三边,∴4﹣1<c<4+1,∴3<c<5,
∵若a,b,c都是正整数,∴c=4,∴△ABC的周长=1+4+4=9
11、阅读下面的解答过程,求的最小值.
解:
∵即的最小值为0
∴的最小值为4.
仿照上面的解答过程,
(1)求的最小值
(2)求的最大值
【解析】(1)
∵
∴
∴的最小值是3.
(2)
∵
∴
∴的最大值为5
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题3 配方法解一元二次方程配方法的应用
1、用配方法解方程,变形后的结果正确的是( )
A. B. C. D.
2、已知方程x2﹣6x﹣2=0,用配方法化为a(x+b)2=c的形式为_____.
3、若把代数式化为的形式,其中、为常数,则______.
4、已知实数a、b、c,满足a2﹣a+b=0,c=4a2﹣4a+b2﹣,则实数c的取值范围是____.
5、用适当的方法解下列方程.
(1); (2).
6、阅读理解:已知,求m 、n的值.
解:∵
∴
∴
∴
∴.
方法应用:(1)已知,求a 、b 的值;
(2)已知 .
①用含 y 的式子表示 x : ;
②若,求 的值.
7、特值验证:
当,0,1,2,5,…时,计算代数式的值,分别得到5,2,1,2,17,….当x的取值发生变化时,代数式的值却有一个确定的范围,通过多次验证可以发现它的值总大于或等于1,所以1就是它的最小值.
变式求证:我们可以用学过的知识,对进行恒等变形:.(注:这种变形方法可称为“配方”) ,.所以无论x取何值,代数式的值不小于1,即最小值为1.
迁移实证:(1)请你用“配方”的方法,确定的最小值为3;
(2)求的最大值.
8、阅读材料:把形如的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即.例如:是的一种形式的配方;所以,,,是的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).请根据阅读材料解决下列问题:
(1)比照上面的例子,写出三种不同形式的配方;
(2)已知,求的值;
(3)已知,求的值.
9、先阅读下面的内容,再解决问题:
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
∵m2+2mn+2n2﹣6n+9=0∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0∴m+n=0,n﹣3=0∴m=﹣3,n=3
根据你的观察,探究下面的问题:
(1)若x2+4x+4+y2﹣8y+16=0,求的值.
(2)试说明不论x,y取什么有理数时,多项式x2+y2﹣2x+2y+3的值总是正数.
(3)已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c比a、b都大,求c的取值范围.
10、若a,b,c为的三边.
(1)化简:|a﹣b+c|+|c﹣a﹣b|﹣|a+b|;
(2)若a,b,c都是正整数,且a2+b2﹣2a﹣8b+17=0,的周长.
11、阅读下面的解答过程,求的最小值.
解:
∵即的最小值为0
∴的最小值为4.
仿照上面的解答过程,
(1)求的最小值
(2)求的最大值
答案版
1、用配方法解方程,变形后的结果正确的是( )
A. B. C. D.
【解析】,
,
,
所以,
故选D.
2、已知方程x2﹣6x﹣2=0,用配方法化为a(x+b)2=c的形式为_____.
【答案】(x﹣3)2=11
【解析】方程x2﹣6x﹣2=0,
移项得:x2﹣6x=2,
配方得:x2﹣6x+9=11,即(x﹣3)2=11.
故答案为:(x﹣3)2=11.
3、若把代数式化为的形式,其中、为常数,则______.
【答案】-7
【解析】x 4x 5=x 4x+4 4 5
=(x 2) 9,
所以m=2,k= 9,
所以m+k=2 9= 7.
故答案为:-7
4、已知实数a、b、c,满足a2﹣a+b=0,c=4a2﹣4a+b2﹣,则实数c的取值范围是____.
【解析】∵a2﹣a+b=0,
∴a2﹣a=﹣b.
∴c=4a2﹣4a+b2﹣=4(a2﹣a)+b2﹣=﹣2b+b2﹣=(b﹣1)2﹣
∵(b﹣1)2≥0,
∴(b﹣1)2﹣≥﹣,即c≥﹣.
5、用适当的方法解下列方程.
(1);
(2).
【解析】(1),
,
,
,
,
所以;
(2)
二次项系数化为1得, ,
移项,得 ,
配方,得 ,
,
6、阅读理解:已知,求m 、n的值.
解:∵
∴
∴
∴
∴.
方法应用:(1)已知,求a 、b 的值;
(2)已知 .
①用含 y 的式子表示 x : ;
②若,求 的值.
【解析】(1)∵a2+b2-10a+4b+29=0,∴(a2-10a+25)+(b2+4b+4)=0,
∴(a-5)2+(b+2)2=0,
∴(a-5)2=0,(b+2)2=0,∴a=5,b=-2;
(2)①∵x+4y=4,
∴x=4-4y;
②∵xy-z2-6z=10,
∴y(4-4y)-z2-6z=10,
∴4y-4y2-z2-6z=10,
∴4y2-4y+z2+6z+10=0,
∴(2y-1)2+(z+3)2=0,
∴y=,z=-3,∴x=2,
∴yx+z的值=()2 3=2.
7、特值验证:
当,0,1,2,5,…时,计算代数式的值,分别得到5,2,1,2,17,….当x的取值发生变化时,代数式的值却有一个确定的范围,通过多次验证可以发现它的值总大于或等于1,所以1就是它的最小值.
变式求证:我们可以用学过的知识,对进行恒等变形:.(注:这种变形方法可称为“配方”) ,.所以无论x取何值,代数式的值不小于1,即最小值为1.
迁移实证:(1)请你用“配方”的方法,确定的最小值为3;
(2)求的最大值.
【解析】(1)证明:
,.所以得最小值为3.
(2)
, ,所以的最大值为.
8、阅读材料:把形如的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即.例如:是的一种形式的配方;所以,,,是的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).请根据阅读材料解决下列问题:
(1)比照上面的例子,写出三种不同形式的配方;
(2)已知,求的值;
(3)已知,求的值.
【解析】(1)的三种配方分别为:
;
;
(或;
(2)∵x2+y2-6x+10y+34=x2-6x+9+y2+10y+25=(x-3)2+(y+5)2=0,
∴x-3=0,y+5=0,
∴x=3,y=-5,
∴3x-2y=3×3-2×(-5)=19
(3)
∴,,
∴,,,
则
9、先阅读下面的内容,再解决问题:
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
∵m2+2mn+2n2﹣6n+9=0∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0∴m+n=0,n﹣3=0∴m=﹣3,n=3
根据你的观察,探究下面的问题:
(1)若x2+4x+4+y2﹣8y+16=0,求的值.
(2)试说明不论x,y取什么有理数时,多项式x2+y2﹣2x+2y+3的值总是正数.
(3)已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c比a、b都大,求c的取值范围.
【解析】(1)已知等式整理得:(x+2)2+(y﹣4)2=0,
可得x+2=0,y﹣4=0,
解得:x=﹣2,y=4,
则;
(2)∵(x﹣1)2≥0,(y+1)2≥0,
∴原式=(x﹣1)2+(y+1)2+1≥1,
则不论x,y取什么有理数时,多项式x2+y2﹣2x+2y+3的值总是正数;
(3)已知等式整理得:(a﹣5)2+(b﹣4)2=0,
可得a﹣5=0,b﹣4=0,
解得:a=5,b=4,
∵
则c的范围是5<c<9.
10、若a,b,c为的三边.
(1)化简:|a﹣b+c|+|c﹣a﹣b|﹣|a+b|;
(2)若a,b,c都是正整数,且a2+b2﹣2a﹣8b+17=0,的周长.
【解析】(1)∵a,b,c为△ABC的三边,
∴a﹣b+c>0,c﹣a﹣b<0,a+b>0,
∴|a﹣b+c|+|c﹣a﹣b|﹣|a+b|=a﹣b+c﹣c+a+b﹣a﹣b=a﹣b;
(2)∵a2+b2﹣2a﹣8b+17=(a2﹣2a+1)+(b2﹣8b+16)=(a﹣1)2+(b﹣4)2=0,∴a=1,b=4,
∵a,b,c为△ABC的三边,∴4﹣1<c<4+1,∴3<c<5,
∵若a,b,c都是正整数,∴c=4,∴△ABC的周长=1+4+4=9
11、阅读下面的解答过程,求的最小值.
解:
∵即的最小值为0
∴的最小值为4.
仿照上面的解答过程,
(1)求的最小值
(2)求的最大值
【解析】(1)
∵
∴
∴的最小值是3.
(2)
∵
∴
∴的最大值为5
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
