13.4 课题学习 最短路径问题公开课课件
文档属性
| 名称 | 13.4 课题学习 最短路径问题公开课课件 |  | |
| 格式 | zip | ||
| 文件大小 | 398.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-05 08:53:17 | ||
图片预览


文档简介
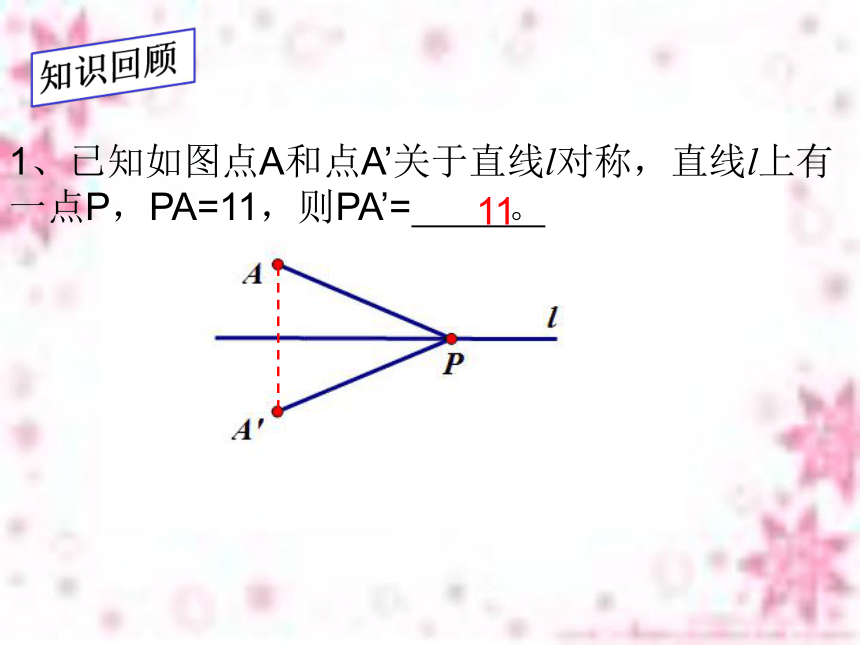
课件19张PPT。13.4 课题学习 最短路径问题知识回顾111、已知如图点A和点A’关于直线l对称,直线l上有一点P,PA=11,则PA’= 。2、如图,在灌溉时需要把河AB中的水引到C处,如何挖渠能使渠道最短?
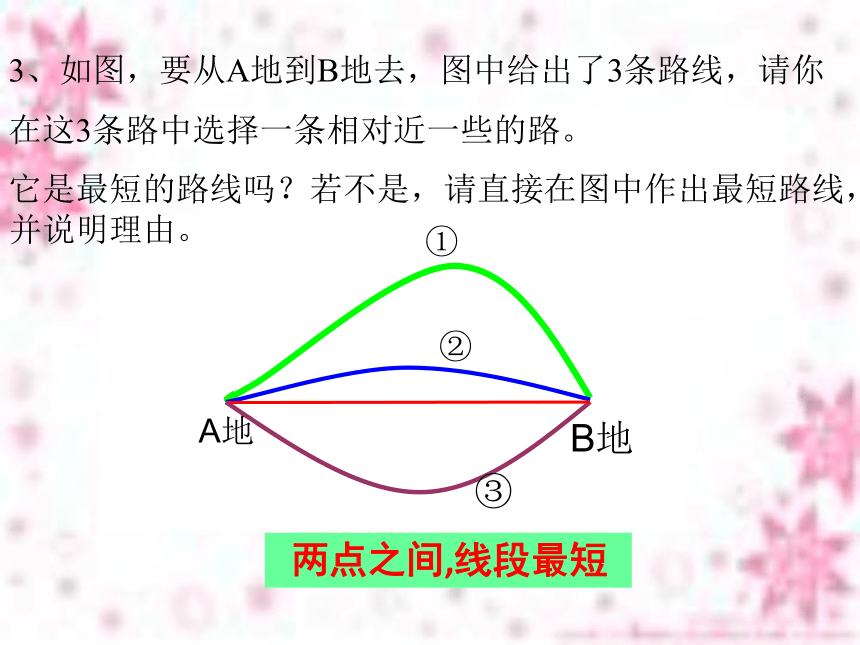
D 垂线段最短3、如图,要从A地到B地去,图中给出了3条路线,请你在这3条路中选择一条相对近一些的路。
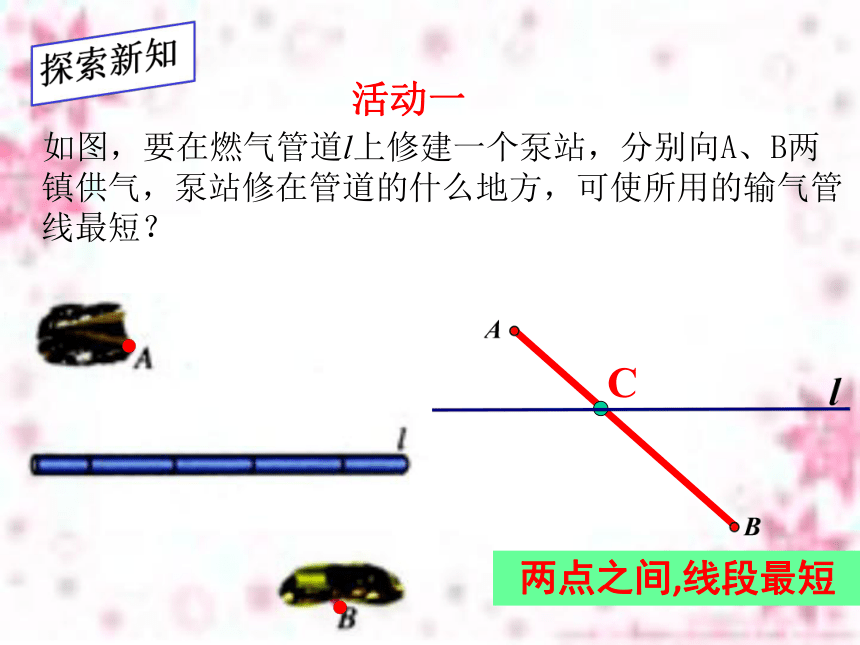
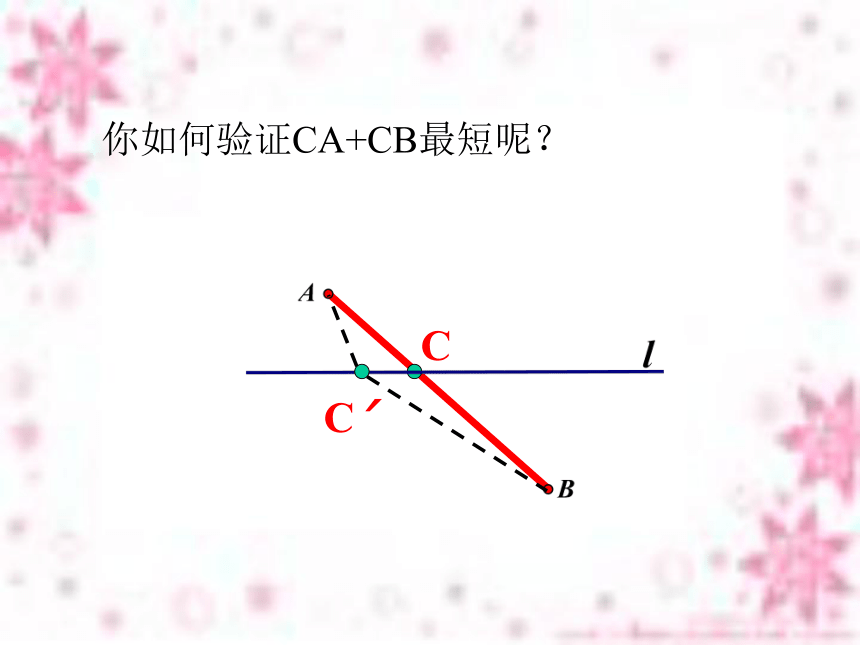
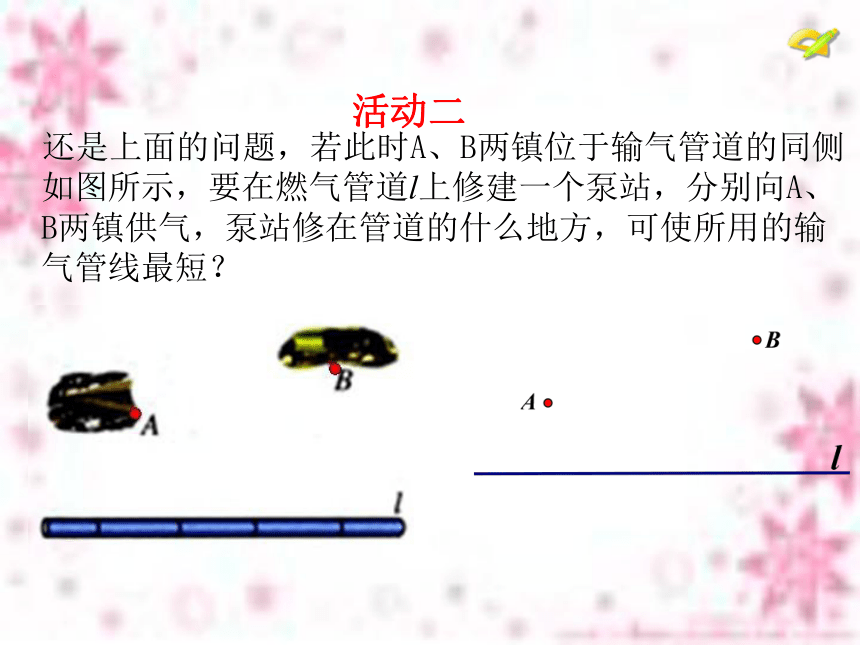
两点之间,线段最短它是最短的路线吗?若不是,请直接在图中作出最短路线,并说明理由。② 如图,要在燃气管道l上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?C 两点之间,线段最短探索新知活动一C你如何验证CA+CB最短呢?
C’活动二 还是上面的问题,若此时A、B两镇位于输气管道的同侧如图所示,要在燃气管道l上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短? 作法:
(1)作点B关于直线l 的对称
点B′;
(2)连接AB′,与直线l 相交
于点C.
则点C 即为所求. 理由:两点之间,线段最短 由轴对称的性质知,
BC = B′C ,BC′=B′C′.
∴ AC +BC = AC +B′C = AB′,
AC′+BC′= AC′+B′C′.
在△AB′C′中,
AB′<AC′+B′C′,
∴ AC +BC<AC′+BC′.
你能用所学的知识证明AC +BC最短吗? 证明:如图,在直线l 上任取一点C′(与点C 不
重合),连接AC′,BC′,B′C′.
即 AC +BC 最短.活动一图对比下活动一,你能找到两个问题的相同点与不同点吗?你有什么启示?活动二图在解决两点在直线同侧的最短路径问题时,我们通常利用轴对称将它转化为两点在直线异侧的问题进行求解。感悟新知1、如图,牧马人从A地出发,到一条笔直的河边l饮马,然后到B地。牧马人到河边的什么地方饮马,可使所走的路径最短?2、如图所示,M、N是△ABC边AB与AC上两点,在BC边上求作一点P,使△PMN的周长最小。
活学活用如图,已知直线MN同侧有两点A、B,在直线MN上求作点P,使得∠APM=∠BPN归纳总结本节课你有什么收获?①学习了利用轴对称解决最短路径问题②感悟和体会转化的思想拓展探索如图,已知牧马营地在P处,每天牧马人要从营地出发赶着马群先到河边饮水,再带到草地吃草,然后回到营地,请你替牧马人设计出最短的放牧路线。河流草地·P营地拓展探索变式:如图,已知牧马营地在P处,牧马人从A地出发要赶着马群先到河边饮水,再带到草地吃草,然后回到营地,请你替牧马人设计出最短的放牧路线。河流草地·P营地·A地
D 垂线段最短3、如图,要从A地到B地去,图中给出了3条路线,请你在这3条路中选择一条相对近一些的路。
两点之间,线段最短它是最短的路线吗?若不是,请直接在图中作出最短路线,并说明理由。② 如图,要在燃气管道l上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?C 两点之间,线段最短探索新知活动一C你如何验证CA+CB最短呢?
C’活动二 还是上面的问题,若此时A、B两镇位于输气管道的同侧如图所示,要在燃气管道l上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短? 作法:
(1)作点B关于直线l 的对称
点B′;
(2)连接AB′,与直线l 相交
于点C.
则点C 即为所求. 理由:两点之间,线段最短 由轴对称的性质知,
BC = B′C ,BC′=B′C′.
∴ AC +BC = AC +B′C = AB′,
AC′+BC′= AC′+B′C′.
在△AB′C′中,
AB′<AC′+B′C′,
∴ AC +BC<AC′+BC′.
你能用所学的知识证明AC +BC最短吗? 证明:如图,在直线l 上任取一点C′(与点C 不
重合),连接AC′,BC′,B′C′.
即 AC +BC 最短.活动一图对比下活动一,你能找到两个问题的相同点与不同点吗?你有什么启示?活动二图在解决两点在直线同侧的最短路径问题时,我们通常利用轴对称将它转化为两点在直线异侧的问题进行求解。感悟新知1、如图,牧马人从A地出发,到一条笔直的河边l饮马,然后到B地。牧马人到河边的什么地方饮马,可使所走的路径最短?2、如图所示,M、N是△ABC边AB与AC上两点,在BC边上求作一点P,使△PMN的周长最小。
活学活用如图,已知直线MN同侧有两点A、B,在直线MN上求作点P,使得∠APM=∠BPN归纳总结本节课你有什么收获?①学习了利用轴对称解决最短路径问题②感悟和体会转化的思想拓展探索如图,已知牧马营地在P处,每天牧马人要从营地出发赶着马群先到河边饮水,再带到草地吃草,然后回到营地,请你替牧马人设计出最短的放牧路线。河流草地·P营地拓展探索变式:如图,已知牧马营地在P处,牧马人从A地出发要赶着马群先到河边饮水,再带到草地吃草,然后回到营地,请你替牧马人设计出最短的放牧路线。河流草地·P营地·A地
