抛物线标准方程
图片预览



文档简介
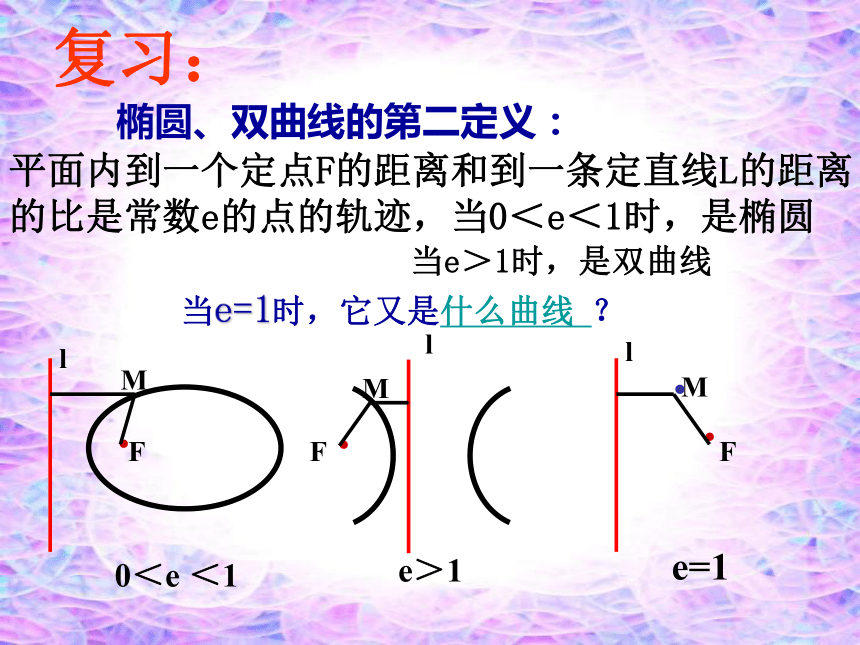
课件19张PPT。抛物线及其标准方程复习:椭圆、双曲线的第二定义:平面内到一个定点F的距离和到一条定直线L的距离
的比是常数e的点的轨迹,当0<e<1时,是椭圆当e>1时,是双曲线当e=1时,它又是什么曲线 ?平面内与一个定点F和一条定直线l
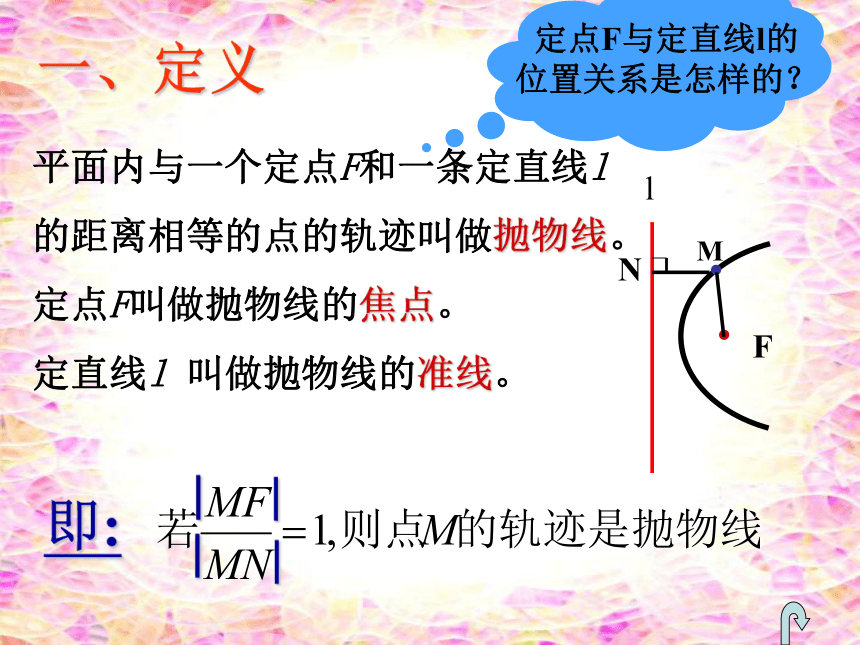
的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
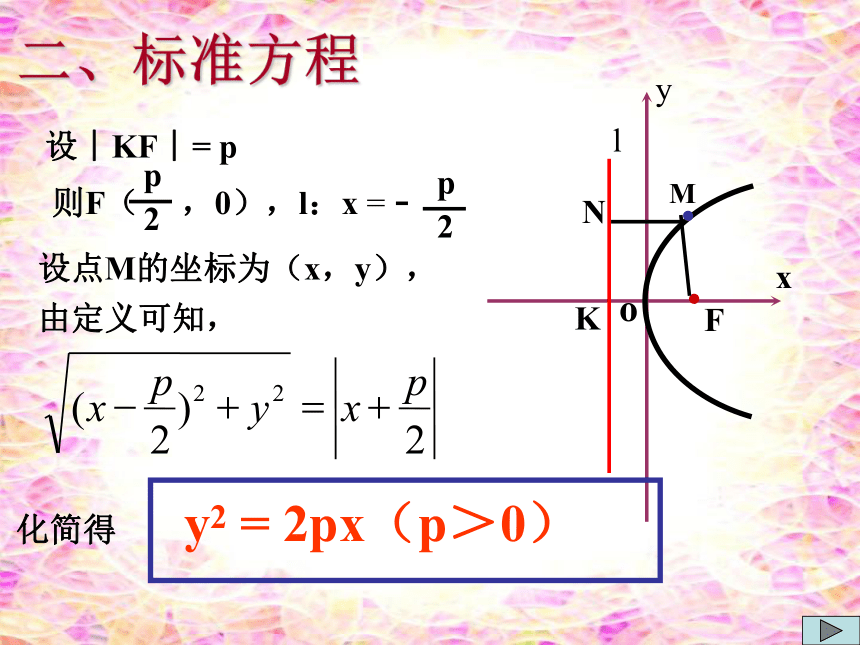
一、定义二、标准方程类比椭圆、双曲线标准方程的建立过程,你认为应如何选择坐标系建立抛物线的方程?二、标准方程K设︱KF︱= p设点M的坐标为(x,y), 由定义可知,方程 y2 = 2px(p>0)
叫做抛物线的标准方程。其中 p 为正常数,它的几何
意义是:
二、标准方程焦点到准线的距离它表示抛物线的焦点在X轴
的正半轴上,焦点F(p/2,0),
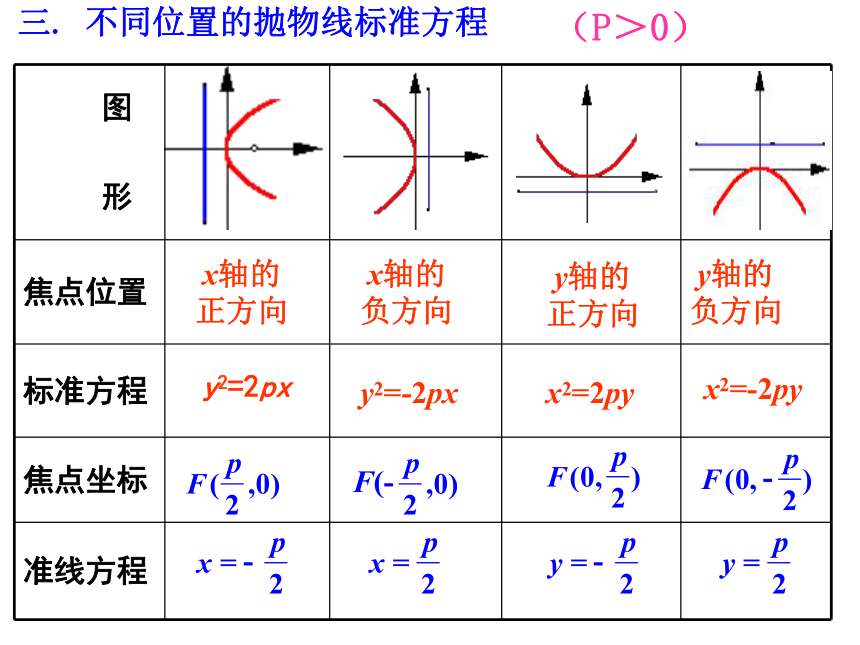
准线方程x=-p/2。 三. 不同位置的抛物线标准方程 x轴的
正方向 x轴的
负方向 y轴的
正方向 y轴的
负方向y2=2pxy2=-2pxx2=2pyx2=-2pyF(----(P>0)1、一次项的变量如为x(或y),
则x轴(或y轴)为抛物线的对
称轴,焦点就在对称轴上。
2、一次项的系数符号决定了开
口方向。一次项的系数除以4可得焦点
坐标的一个值。 【小结1】【小结2】
①在抛物线的的标准方程中p的几何意义是
;
②抛物线y2=ax(a?0)的焦点坐标是 、
抛物线x2=ay(a?0)的焦点坐标是 .
抛物线y=ax2(a?0)的焦点坐标是 ,
准线方程是 。
M是抛物线y2 = 2px(P>0)上一点,若点
M 的横坐标为X0,则点M到焦点的距离是_________焦点到准线的距离与a 的正
负无关例1、(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。确定方程形式思维程序由已知确定开口方向求出P值写出抛物线标准方程定性定量例2、求过点A(-3,2)的抛物线的
标准方程。解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p= 当焦点在x轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
练习:1、根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0);(2)准线方程 是y = ;(3)焦点到准线的距离是2。y2 =12xx2 =yy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y(4)焦点在直线x-2y-4=0上。y2 =16x或x2 =-8y2、求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)x2= y
(3)2y2 +5x =0 (4)x2 +8y =0(5,0)x= -5(0,-2)y=23、若抛物线y2=2x上的两点A、B到焦点的距离之和为5,则线段AB的中点到y轴的距离为 。24、若抛物线y2=x上一点P到A(3,-1)的距离与到焦点F的距离之和最小,则P点的坐标为 。(1,-1)5. (2006山东卷)
已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,
则y12+y22的最小值是 .32小 结 :2、抛物线的定义,标准方程类型与图象的
对应关系以及判断方法3、已知抛物线的标准方程求它的焦点、
准线方程4、已知抛物线的焦点或准线方程,
求抛物线的标准方程,常用方法:
(1)用定义 ;
(2)用待定系数法。本节主要学习内容1、椭圆、双曲线与抛物线的定义的联系
及其区别;作业P69、1,3,4.P65练习3,4 谢 谢 指 导
制作与主讲:湛江一中 杨善茂
的比是常数e的点的轨迹,当0<e<1时,是椭圆当e>1时,是双曲线当e=1时,它又是什么曲线 ?平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
一、定义二、标准方程类比椭圆、双曲线标准方程的建立过程,你认为应如何选择坐标系建立抛物线的方程?二、标准方程K设︱KF︱= p设点M的坐标为(x,y), 由定义可知,方程 y2 = 2px(p>0)
叫做抛物线的标准方程。其中 p 为正常数,它的几何
意义是:
二、标准方程焦点到准线的距离它表示抛物线的焦点在X轴
的正半轴上,焦点F(p/2,0),
准线方程x=-p/2。 三. 不同位置的抛物线标准方程 x轴的
正方向 x轴的
负方向 y轴的
正方向 y轴的
负方向y2=2pxy2=-2pxx2=2pyx2=-2pyF(----(P>0)1、一次项的变量如为x(或y),
则x轴(或y轴)为抛物线的对
称轴,焦点就在对称轴上。
2、一次项的系数符号决定了开
口方向。一次项的系数除以4可得焦点
坐标的一个值。 【小结1】【小结2】
①在抛物线的的标准方程中p的几何意义是
;
②抛物线y2=ax(a?0)的焦点坐标是 、
抛物线x2=ay(a?0)的焦点坐标是 .
抛物线y=ax2(a?0)的焦点坐标是 ,
准线方程是 。
M是抛物线y2 = 2px(P>0)上一点,若点
M 的横坐标为X0,则点M到焦点的距离是_________焦点到准线的距离与a 的正
负无关例1、(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。确定方程形式思维程序由已知确定开口方向求出P值写出抛物线标准方程定性定量例2、求过点A(-3,2)的抛物线的
标准方程。解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p= 当焦点在x轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
练习:1、根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0);(2)准线方程 是y = ;(3)焦点到准线的距离是2。y2 =12xx2 =yy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y(4)焦点在直线x-2y-4=0上。y2 =16x或x2 =-8y2、求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)x2= y
(3)2y2 +5x =0 (4)x2 +8y =0(5,0)x= -5(0,-2)y=23、若抛物线y2=2x上的两点A、B到焦点的距离之和为5,则线段AB的中点到y轴的距离为 。24、若抛物线y2=x上一点P到A(3,-1)的距离与到焦点F的距离之和最小,则P点的坐标为 。(1,-1)5. (2006山东卷)
已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,
则y12+y22的最小值是 .32小 结 :2、抛物线的定义,标准方程类型与图象的
对应关系以及判断方法3、已知抛物线的标准方程求它的焦点、
准线方程4、已知抛物线的焦点或准线方程,
求抛物线的标准方程,常用方法:
(1)用定义 ;
(2)用待定系数法。本节主要学习内容1、椭圆、双曲线与抛物线的定义的联系
及其区别;作业P69、1,3,4.P65练习3,4 谢 谢 指 导
制作与主讲:湛江一中 杨善茂
