21.3 实际问题与一元二次方程 动态几何问题同步练习(含答案)
文档属性
| 名称 | 21.3 实际问题与一元二次方程 动态几何问题同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-20 17:26:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题5 一元二次方程实际问题的应用-动态几何问题
1、如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P,Q分别从点A,B同时开始移动,点P的速度为1cm/秒,点Q的速度为2cm/秒,点Q移动到点C后停止,点P也随之停止运动.下列时间瞬间中,能使△PBQ的面积为15cm2的是( )
A.2秒钟 B.3秒钟 C.4秒钟 D.5秒钟
2、如图,AB⊥BC,AB=10 cm,BC=8 cm,一只蝉从C点沿CB方向以每秒1 cm的速度爬行,蝉开始爬行的同时,一只螳螂由A点沿AB方向以每秒2 cm的速度爬行,当螳螂和蝉爬行x秒后,它们分别到达了M,N的位置,此时,△MNB的面积恰好为24 cm2,由题意可列方程( )
A.2x·x=24 B.(10-2x)(8-x)=24
C.(10-x)(8-2x)=24 D.(10-2x)(8-x)=48
3、如图,在中,,,,点P从点A开始沿AC 边向点C以的速度匀速移动,同时另一点Q由C点开始以的速度沿着射线CB匀速移动,当的面积等于运动时间为
A.5秒 B.20秒 C.5秒或20秒 D.不确定
4、如图,△ABC中, AB =AC=24 cm, BC=16cm,AD= BD.如果点P在线段BC上以 2 cm/s 的速度由B点向C点运动,同时,点 Q在线段CA上以v cm/s 的速度由C点向A点运动,那么当△BPD 与△CQP全等时,v =( )
A.3 B.4 C.2或 4 D.2或3
5、如图,将边长为12 cm的正方形ABCD沿其对角线AC剪开,再把ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为32 cm2,则它移动的距离AA′等于 _________
6、如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=8cm,动点P,Q分别从点A、C同时出发,点P以3cm/S的速度向B移动,一直到达B为止;点Q以2cm/s的速度向D移动.当P、Q两点从出发开始到_____秒时,点P和点Q的距离是10cm.
7、如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边BC上,从点C向点B移动,若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是_____.
8、在平面直角坐标系O中,过原点O及点A(0,2) 、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D 点P从点O出发,以每秒个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动 设移动时间为t秒,当t为 时,△PQB为直角三角形.
9、如图,长方形中,,,动点、分别从点、同时出发,点以2厘米/秒的速度向终点移动,点以1厘米/秒的速度向移动,当有一点到达终点时,另一点也停止运动.设运动的时间为秒,当________时,以点、、为顶点的三角形是等腰三角形.
10、△ABC中,∠B=90°,AB=9,BC=12,点p从点A开始延边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果P.Q分别从A.B同时出发,当点Q运动到点C时,两点停止运动,问:
(1)填空:BQ=______,PB=______(用含t的代数式表示)
(2)经过几秒,PQ的长为 cm?
(3)经过几秒,的面积等于
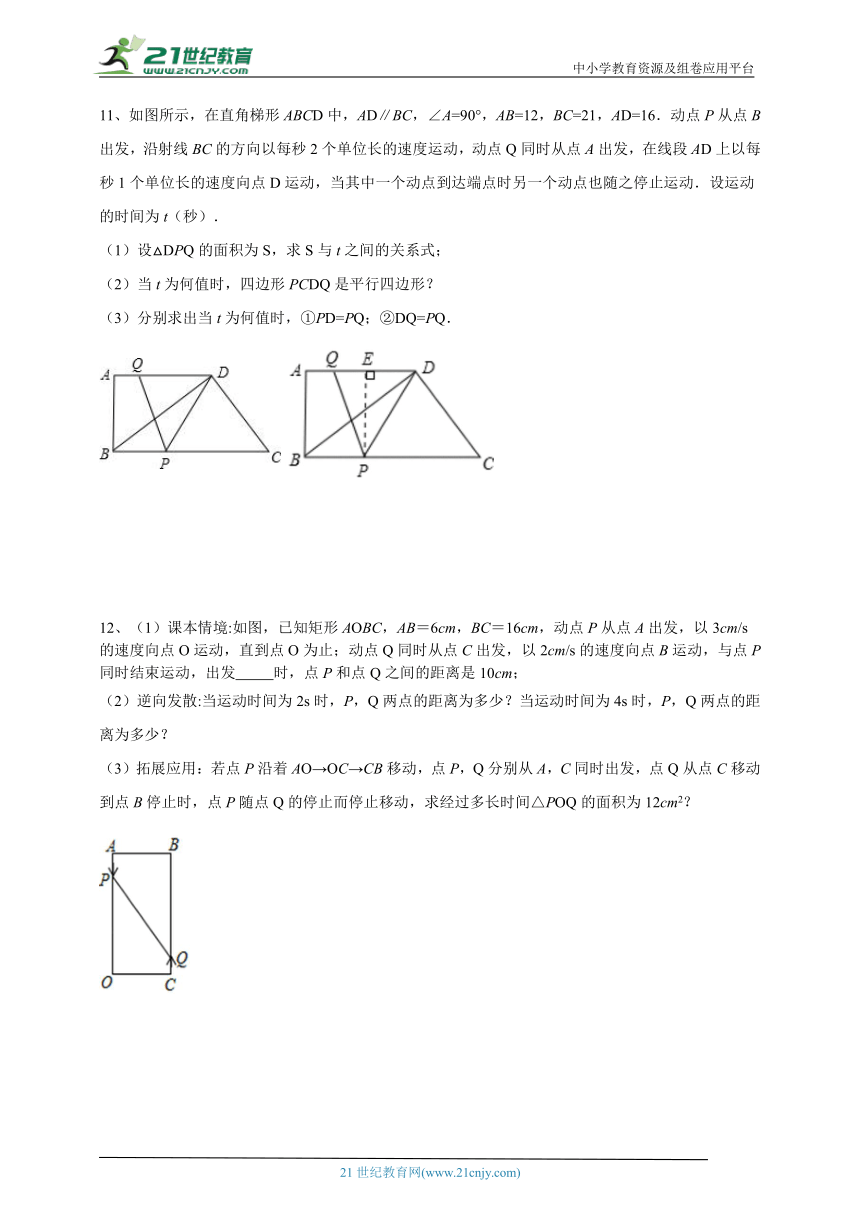
11、如图所示,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
(1)设△DPQ的面积为S,求S与t之间的关系式;
(2)当t为何值时,四边形PCDQ是平行四边形?
(3)分别求出当t为何值时,①PD=PQ;②DQ=PQ.
12、(1)课本情境:如图,已知矩形AOBC,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动,出发 时,点P和点Q之间的距离是10cm;
(2)逆向发散:当运动时间为2s时,P,Q两点的距离为多少?当运动时间为4s时,P,Q两点的距离为多少?
(3)拓展应用:若点P沿着AO→OC→CB移动,点P,Q分别从A,C同时出发,点Q从点C移动到点B停止时,点P随点Q的停止而停止移动,求经过多长时间△POQ的面积为12cm2?
答案版
1、如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P,Q分别从点A,B同时开始移动,点P的速度为1cm/秒,点Q的速度为2cm/秒,点Q移动到点C后停止,点P也随之停止运动.下列时间瞬间中,能使△PBQ的面积为15cm2的是( )
A.2秒钟 B.3秒钟 C.4秒钟 D.5秒钟
【解析】设动点P,Q运动t秒后,能使△PBQ的面积为15cm2,则BP为(8﹣t)cm,BQ为2tcm,由三角形的面积计算公式列方程得:×(8﹣t)×2t=15,解得t1=3,t2=5(当t=5时,BQ=10,不合题意,舍去).故当动点P,Q运动3秒时,能使△PBQ的面积为15cm2.
故选B.
2、如图,AB⊥BC,AB=10 cm,BC=8 cm,一只蝉从C点沿CB方向以每秒1 cm的速度爬行,蝉开始爬行的同时,一只螳螂由A点沿AB方向以每秒2 cm的速度爬行,当螳螂和蝉爬行x秒后,它们分别到达了M,N的位置,此时,△MNB的面积恰好为24 cm2,由题意可列方程( )
A.2x·x=24 B.(10-2x)(8-x)=24
C.(10-x)(8-2x)=24 D.(10-2x)(8-x)=48
【解析】设x秒后,螳螂走了 2x,蝉走了x,MB=10-2x,NC=8-x,
由题意知(10-2x)(8-x)=24,
(10-2x)(8-x)=48,选D.
3、如图,在中,,,,点P从点A开始沿AC 边向点C以的速度匀速移动,同时另一点Q由C点开始以的速度沿着射线CB匀速移动,当的面积等于运动时间为
A.5秒 B.20秒 C.5秒或20秒 D.不确定
【解析】由题意得:AP=2t,CQ=3t,∴PC=50﹣2t,∴ PC CQ=300,∴ (50﹣2t) 3t=300,解得:t=20或5,∴t=20s或5s时,△PCQ的面积为300m2.故选C.
【小结】本题考查了一元二次方程的应用,三角形的面积公式等知识,解题的关键是把问题转化为方程,属于基础题,中考常考题型.
4、如图,△ABC中, AB =AC=24 cm, BC=16cm,AD= BD.如果点P在线段BC上以 2 cm/s 的速度由B点向C点运动,同时,点 Q在线段CA上以v cm/s 的速度由C点向A点运动,那么当△BPD 与△CQP全等时,v =( )
A.3 B.4 C.2或 4 D.2或3
【解析】∵△ABC中,AB=AC=24厘米,点D为AB的中点,∴BD=12厘米,
情况一:若△BPD≌△CPQ,则需BD=CQ=12厘米,BP=CP=BC=×16=8(厘米)
∵点Q的运动速度为2厘米/秒,∴点Q的运动时间为:8÷2=4(s),∴v=CQ÷4= 12÷4=3(厘米/秒);
情况二:
②若△BPD≌△CQP,则CP=BD=12厘米,BP=CQ,
得出,解得:解出即可.
因此v的值为:2厘米/秒或3厘米/秒,
故选:D.
5、如图,将边长为12 cm的正方形ABCD沿其对角线AC剪开,再把ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为32 cm2,则它移动的距离AA′等于 _________
【解析】
设AA′=xcm,则A′D=(12-x)cm,∵正方形ABCD,∴∠D=90°,AD=CD,∴∠DAC=45°,同理可证∠B′A′C′=45°,∵△A′B′C′由△ABC沿着AD方向平移得到,∴A′B′⊥AD,∴∠A′EA=45°,∴∠B′A′C′=∠A′EA,∴A′F∥EC,∵A′E∥CF,∴四边形A′ECF为平行四边形,所以SA′ECF= A′E×A′D=x(12-x)=32,解得x=4或8.
6、如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=8cm,动点P,Q分别从点A、C同时出发,点P以3cm/S的速度向B移动,一直到达B为止;点Q以2cm/s的速度向D移动.当P、Q两点从出发开始到_____秒时,点P和点Q的距离是10cm.
【解析】
设当P、Q两点从出发开始到t秒时,点P和点Q的距离是10cm,
如图,作PE⊥CD于E,
则PE=AD=8cm,
∵DE=AP=3t,CQ=2t,
∴EQ=CD-DE-CQ=,
由勾股定理得:(16-5t)2+62=102,
解得t1=2,t2=.
7、如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边BC上,从点C向点B移动,若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是_____.
【解析】∵AP=CQ=t,∴CP=6-t,
∴PQ==
∵0≤t≤2,∴当t=2时,PQ的值最小,
∴线段PQ的最小值是2.
8、在平面直角坐标系O中,过原点O及点A(0,2) 、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D 点P从点O出发,以每秒个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动 设移动时间为t秒,当t为 时,△PQB为直角三角形.
【解析】由题易知,B(6,2),P(t,t),Q(2t,0)
则BP2=(6-t)2+(2-t)2;BQ2=(6-2t)2+4;PQ2=2t2;
当△PQB为直角三角形时,
①BP2=BQ2+ PQ2时, (6-t)2+(2-t)2=(6-2t)2+4+2t2
解得t=2;t=0(舍去)
②BP2+BQ2= PQ2时, (6-t)2+(2-t)2+(6-2t)2+4=2t2
解得:
②BP2+PQ2=BQ2时, (6-t)2+(2-t)2+2t2= (6-2t)2+4
解得:t=0(舍去)
综上,t=;t=2
考点:1 两点之间的距离;2 一元二次方程的解法;3 直角三角形
9、如图,长方形中,,,动点、分别从点、同时出发,点以2厘米/秒的速度向终点移动,点以1厘米/秒的速度向移动,当有一点到达终点时,另一点也停止运动.设运动的时间为秒,当________时,以点、、为顶点的三角形是等腰三角形.
【解析】如图1,当PQ=DQ时,作QE⊥AB于E,∴∠PEQ=90°,
∵∠B=∠C=90°,∴四边形BCQE是矩形,∴QE=BC=2cm,BE=CQ=t.
∵AP=2t,∴PE=6﹣2t﹣t=6﹣3t.DQ=6﹣t.
∵PQ=DQ,∴PQ=6﹣t.
在RtPQE中,由勾股定理,得(6﹣3t)2+4=(6﹣t)2,解得:t=.
如图2,当PD=PQ时,作PE⊥DQ于E,
∴DE=QE=DQ,∠PED=90°.
∵∠B=∠C=90°,∴四边形BCQE是矩形,∴PE=BC=2cm.
∵DQ=6﹣t,∴DE=.∴2t=,解得:t=;
如图5,当PD=QD时,
∵AP=2t,CQ=t,∴DQ=6﹣t,∴PD=6﹣t.
在RtAPD中,由勾股定理,得4+4t2=(6﹣t)2,
解得t1=,t2=(舍去).
综上所述:t=,,,.
10、△ABC中,∠B=90°,AB=9,BC=12,点p从点A开始延边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果P.Q分别从A.B同时出发,当点Q运动到点C时,两点停止运动,问:
(1)填空:BQ=______,PB=______(用含t的代数式表示)
(2)经过几秒,PQ的长为 cm?
(3)经过几秒,的面积等于
【解析】(1)2t,9 – t.
(2)由题意得:(9-t)2+(2t)2=72,
解得:t1=,t2=3;
(3)S△PBQ =×BP×BQ =×(9-t)×2t=8,
解得:t1=8,t2=1.
∵0≤t≤6,
∴t=1 .
11、如图所示,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
(1)设△DPQ的面积为S,求S与t之间的关系式;
(2)当t为何值时,四边形PCDQ是平行四边形?
(3)分别求出当t为何值时,①PD=PQ;②DQ=PQ.
【解析】(1)在直角梯形ABCD中,AD∥BC,∠A=90°,BC=21,AB=12,AD=16,
设AQ=t,BP=2t,则DQ=16 t,PC=21 2t,
过点P作PE⊥AD于E,则四边形ABPE是矩形,PE=AB=12,
∴S=DQ AB=(16 t)×12= 6t+96
(2)当四边形PCDQ是平行四边形时,PC=DQ,∴21 2t=16 t解得:t=5,
∴当t=5时,四边形PCDQ是平行四边形.
(3)∵AE=BP=2t,PE=AB=12,
①当PD=PQ时,QE=ED=QD,
∵DE=16 2t,∴AE=BP=AQ+QE,即2t=t+16 2t,解得:t=,∴当t=时,PD=PQ
②当DQ=PQ时,DQ2=PQ2
∴t2+122=(16 t)2解得:t=,∴当t=时,DQ=PQ
12、(1)课本情境:如图,已知矩形AOBC,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动,出发 时,点P和点Q之间的距离是10cm;
(2)逆向发散:当运动时间为2s时,P,Q两点的距离为多少?当运动时间为4s时,P,Q两点的距离为多少?
(3)拓展应用:若点P沿着AO→OC→CB移动,点P,Q分别从A,C同时出发,点Q从点C移动到点B停止时,点P随点Q的停止而停止移动,求经过多长时间△POQ的面积为12cm2?
【解析】(1)设运动时间为t秒时,如图,过点P作PE⊥BC于E,
由运动知,AP=3t,CQ=2t,PE=6,EQ=16﹣3t﹣2t=16﹣5t,
∵点P和点Q之间的距离是10 cm,∴62+(16﹣5t)2=100,
解得t1=,t2=,
∴t=或.
(2)t=2时,由运动知AP=3×2=6 cm,CQ=2×2=4 cm,
∴四边形APEB是矩形,∴PE=AB=6,BE=6,
∴EQ=BC﹣BE﹣CQ=16﹣6﹣4=6,
根据勾股定理得PQ=,
∴当t=2 s时,P,Q两点的距离为6 cm;
当t=4 s时,由运动知AP=3×4=12 cm,CQ=2×4=8cm,
∴四边形APEB是矩形,
∴PE=AB=6,BQ=8,CE=OP=4
∴EQ=BC﹣CE﹣BQ=16﹣4﹣8=4,
根据勾股定理得PQ=,
P,Q两点的距离为2cm.
(3)点Q从C点移动到B点所花的时间为16÷2=8s,
当点P在AO上时,S△POQ===12,
解得t=4.
当点P在OC上时,S△POQ===12,
解得t=6或﹣(舍弃).
当点P在CB上时,S△POQ===12,
解得t=18>8(不符合题意舍弃),
综上所述,经过4 s或6 s时,△POQ的面积为12 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题5 一元二次方程实际问题的应用-动态几何问题
1、如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P,Q分别从点A,B同时开始移动,点P的速度为1cm/秒,点Q的速度为2cm/秒,点Q移动到点C后停止,点P也随之停止运动.下列时间瞬间中,能使△PBQ的面积为15cm2的是( )
A.2秒钟 B.3秒钟 C.4秒钟 D.5秒钟
2、如图,AB⊥BC,AB=10 cm,BC=8 cm,一只蝉从C点沿CB方向以每秒1 cm的速度爬行,蝉开始爬行的同时,一只螳螂由A点沿AB方向以每秒2 cm的速度爬行,当螳螂和蝉爬行x秒后,它们分别到达了M,N的位置,此时,△MNB的面积恰好为24 cm2,由题意可列方程( )
A.2x·x=24 B.(10-2x)(8-x)=24
C.(10-x)(8-2x)=24 D.(10-2x)(8-x)=48
3、如图,在中,,,,点P从点A开始沿AC 边向点C以的速度匀速移动,同时另一点Q由C点开始以的速度沿着射线CB匀速移动,当的面积等于运动时间为
A.5秒 B.20秒 C.5秒或20秒 D.不确定
4、如图,△ABC中, AB =AC=24 cm, BC=16cm,AD= BD.如果点P在线段BC上以 2 cm/s 的速度由B点向C点运动,同时,点 Q在线段CA上以v cm/s 的速度由C点向A点运动,那么当△BPD 与△CQP全等时,v =( )
A.3 B.4 C.2或 4 D.2或3
5、如图,将边长为12 cm的正方形ABCD沿其对角线AC剪开,再把ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为32 cm2,则它移动的距离AA′等于 _________
6、如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=8cm,动点P,Q分别从点A、C同时出发,点P以3cm/S的速度向B移动,一直到达B为止;点Q以2cm/s的速度向D移动.当P、Q两点从出发开始到_____秒时,点P和点Q的距离是10cm.
7、如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边BC上,从点C向点B移动,若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是_____.
8、在平面直角坐标系O中,过原点O及点A(0,2) 、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D 点P从点O出发,以每秒个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动 设移动时间为t秒,当t为 时,△PQB为直角三角形.
9、如图,长方形中,,,动点、分别从点、同时出发,点以2厘米/秒的速度向终点移动,点以1厘米/秒的速度向移动,当有一点到达终点时,另一点也停止运动.设运动的时间为秒,当________时,以点、、为顶点的三角形是等腰三角形.
10、△ABC中,∠B=90°,AB=9,BC=12,点p从点A开始延边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果P.Q分别从A.B同时出发,当点Q运动到点C时,两点停止运动,问:
(1)填空:BQ=______,PB=______(用含t的代数式表示)
(2)经过几秒,PQ的长为 cm?
(3)经过几秒,的面积等于
11、如图所示,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
(1)设△DPQ的面积为S,求S与t之间的关系式;
(2)当t为何值时,四边形PCDQ是平行四边形?
(3)分别求出当t为何值时,①PD=PQ;②DQ=PQ.
12、(1)课本情境:如图,已知矩形AOBC,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动,出发 时,点P和点Q之间的距离是10cm;
(2)逆向发散:当运动时间为2s时,P,Q两点的距离为多少?当运动时间为4s时,P,Q两点的距离为多少?
(3)拓展应用:若点P沿着AO→OC→CB移动,点P,Q分别从A,C同时出发,点Q从点C移动到点B停止时,点P随点Q的停止而停止移动,求经过多长时间△POQ的面积为12cm2?
答案版
1、如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P,Q分别从点A,B同时开始移动,点P的速度为1cm/秒,点Q的速度为2cm/秒,点Q移动到点C后停止,点P也随之停止运动.下列时间瞬间中,能使△PBQ的面积为15cm2的是( )
A.2秒钟 B.3秒钟 C.4秒钟 D.5秒钟
【解析】设动点P,Q运动t秒后,能使△PBQ的面积为15cm2,则BP为(8﹣t)cm,BQ为2tcm,由三角形的面积计算公式列方程得:×(8﹣t)×2t=15,解得t1=3,t2=5(当t=5时,BQ=10,不合题意,舍去).故当动点P,Q运动3秒时,能使△PBQ的面积为15cm2.
故选B.
2、如图,AB⊥BC,AB=10 cm,BC=8 cm,一只蝉从C点沿CB方向以每秒1 cm的速度爬行,蝉开始爬行的同时,一只螳螂由A点沿AB方向以每秒2 cm的速度爬行,当螳螂和蝉爬行x秒后,它们分别到达了M,N的位置,此时,△MNB的面积恰好为24 cm2,由题意可列方程( )
A.2x·x=24 B.(10-2x)(8-x)=24
C.(10-x)(8-2x)=24 D.(10-2x)(8-x)=48
【解析】设x秒后,螳螂走了 2x,蝉走了x,MB=10-2x,NC=8-x,
由题意知(10-2x)(8-x)=24,
(10-2x)(8-x)=48,选D.
3、如图,在中,,,,点P从点A开始沿AC 边向点C以的速度匀速移动,同时另一点Q由C点开始以的速度沿着射线CB匀速移动,当的面积等于运动时间为
A.5秒 B.20秒 C.5秒或20秒 D.不确定
【解析】由题意得:AP=2t,CQ=3t,∴PC=50﹣2t,∴ PC CQ=300,∴ (50﹣2t) 3t=300,解得:t=20或5,∴t=20s或5s时,△PCQ的面积为300m2.故选C.
【小结】本题考查了一元二次方程的应用,三角形的面积公式等知识,解题的关键是把问题转化为方程,属于基础题,中考常考题型.
4、如图,△ABC中, AB =AC=24 cm, BC=16cm,AD= BD.如果点P在线段BC上以 2 cm/s 的速度由B点向C点运动,同时,点 Q在线段CA上以v cm/s 的速度由C点向A点运动,那么当△BPD 与△CQP全等时,v =( )
A.3 B.4 C.2或 4 D.2或3
【解析】∵△ABC中,AB=AC=24厘米,点D为AB的中点,∴BD=12厘米,
情况一:若△BPD≌△CPQ,则需BD=CQ=12厘米,BP=CP=BC=×16=8(厘米)
∵点Q的运动速度为2厘米/秒,∴点Q的运动时间为:8÷2=4(s),∴v=CQ÷4= 12÷4=3(厘米/秒);
情况二:
②若△BPD≌△CQP,则CP=BD=12厘米,BP=CQ,
得出,解得:解出即可.
因此v的值为:2厘米/秒或3厘米/秒,
故选:D.
5、如图,将边长为12 cm的正方形ABCD沿其对角线AC剪开,再把ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为32 cm2,则它移动的距离AA′等于 _________
【解析】
设AA′=xcm,则A′D=(12-x)cm,∵正方形ABCD,∴∠D=90°,AD=CD,∴∠DAC=45°,同理可证∠B′A′C′=45°,∵△A′B′C′由△ABC沿着AD方向平移得到,∴A′B′⊥AD,∴∠A′EA=45°,∴∠B′A′C′=∠A′EA,∴A′F∥EC,∵A′E∥CF,∴四边形A′ECF为平行四边形,所以SA′ECF= A′E×A′D=x(12-x)=32,解得x=4或8.
6、如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=8cm,动点P,Q分别从点A、C同时出发,点P以3cm/S的速度向B移动,一直到达B为止;点Q以2cm/s的速度向D移动.当P、Q两点从出发开始到_____秒时,点P和点Q的距离是10cm.
【解析】
设当P、Q两点从出发开始到t秒时,点P和点Q的距离是10cm,
如图,作PE⊥CD于E,
则PE=AD=8cm,
∵DE=AP=3t,CQ=2t,
∴EQ=CD-DE-CQ=,
由勾股定理得:(16-5t)2+62=102,
解得t1=2,t2=.
7、如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边BC上,从点C向点B移动,若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是_____.
【解析】∵AP=CQ=t,∴CP=6-t,
∴PQ==
∵0≤t≤2,∴当t=2时,PQ的值最小,
∴线段PQ的最小值是2.
8、在平面直角坐标系O中,过原点O及点A(0,2) 、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D 点P从点O出发,以每秒个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动 设移动时间为t秒,当t为 时,△PQB为直角三角形.
【解析】由题易知,B(6,2),P(t,t),Q(2t,0)
则BP2=(6-t)2+(2-t)2;BQ2=(6-2t)2+4;PQ2=2t2;
当△PQB为直角三角形时,
①BP2=BQ2+ PQ2时, (6-t)2+(2-t)2=(6-2t)2+4+2t2
解得t=2;t=0(舍去)
②BP2+BQ2= PQ2时, (6-t)2+(2-t)2+(6-2t)2+4=2t2
解得:
②BP2+PQ2=BQ2时, (6-t)2+(2-t)2+2t2= (6-2t)2+4
解得:t=0(舍去)
综上,t=;t=2
考点:1 两点之间的距离;2 一元二次方程的解法;3 直角三角形
9、如图,长方形中,,,动点、分别从点、同时出发,点以2厘米/秒的速度向终点移动,点以1厘米/秒的速度向移动,当有一点到达终点时,另一点也停止运动.设运动的时间为秒,当________时,以点、、为顶点的三角形是等腰三角形.
【解析】如图1,当PQ=DQ时,作QE⊥AB于E,∴∠PEQ=90°,
∵∠B=∠C=90°,∴四边形BCQE是矩形,∴QE=BC=2cm,BE=CQ=t.
∵AP=2t,∴PE=6﹣2t﹣t=6﹣3t.DQ=6﹣t.
∵PQ=DQ,∴PQ=6﹣t.
在RtPQE中,由勾股定理,得(6﹣3t)2+4=(6﹣t)2,解得:t=.
如图2,当PD=PQ时,作PE⊥DQ于E,
∴DE=QE=DQ,∠PED=90°.
∵∠B=∠C=90°,∴四边形BCQE是矩形,∴PE=BC=2cm.
∵DQ=6﹣t,∴DE=.∴2t=,解得:t=;
如图5,当PD=QD时,
∵AP=2t,CQ=t,∴DQ=6﹣t,∴PD=6﹣t.
在RtAPD中,由勾股定理,得4+4t2=(6﹣t)2,
解得t1=,t2=(舍去).
综上所述:t=,,,.
10、△ABC中,∠B=90°,AB=9,BC=12,点p从点A开始延边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果P.Q分别从A.B同时出发,当点Q运动到点C时,两点停止运动,问:
(1)填空:BQ=______,PB=______(用含t的代数式表示)
(2)经过几秒,PQ的长为 cm?
(3)经过几秒,的面积等于
【解析】(1)2t,9 – t.
(2)由题意得:(9-t)2+(2t)2=72,
解得:t1=,t2=3;
(3)S△PBQ =×BP×BQ =×(9-t)×2t=8,
解得:t1=8,t2=1.
∵0≤t≤6,
∴t=1 .
11、如图所示,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
(1)设△DPQ的面积为S,求S与t之间的关系式;
(2)当t为何值时,四边形PCDQ是平行四边形?
(3)分别求出当t为何值时,①PD=PQ;②DQ=PQ.
【解析】(1)在直角梯形ABCD中,AD∥BC,∠A=90°,BC=21,AB=12,AD=16,
设AQ=t,BP=2t,则DQ=16 t,PC=21 2t,
过点P作PE⊥AD于E,则四边形ABPE是矩形,PE=AB=12,
∴S=DQ AB=(16 t)×12= 6t+96
(2)当四边形PCDQ是平行四边形时,PC=DQ,∴21 2t=16 t解得:t=5,
∴当t=5时,四边形PCDQ是平行四边形.
(3)∵AE=BP=2t,PE=AB=12,
①当PD=PQ时,QE=ED=QD,
∵DE=16 2t,∴AE=BP=AQ+QE,即2t=t+16 2t,解得:t=,∴当t=时,PD=PQ
②当DQ=PQ时,DQ2=PQ2
∴t2+122=(16 t)2解得:t=,∴当t=时,DQ=PQ
12、(1)课本情境:如图,已知矩形AOBC,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动,出发 时,点P和点Q之间的距离是10cm;
(2)逆向发散:当运动时间为2s时,P,Q两点的距离为多少?当运动时间为4s时,P,Q两点的距离为多少?
(3)拓展应用:若点P沿着AO→OC→CB移动,点P,Q分别从A,C同时出发,点Q从点C移动到点B停止时,点P随点Q的停止而停止移动,求经过多长时间△POQ的面积为12cm2?
【解析】(1)设运动时间为t秒时,如图,过点P作PE⊥BC于E,
由运动知,AP=3t,CQ=2t,PE=6,EQ=16﹣3t﹣2t=16﹣5t,
∵点P和点Q之间的距离是10 cm,∴62+(16﹣5t)2=100,
解得t1=,t2=,
∴t=或.
(2)t=2时,由运动知AP=3×2=6 cm,CQ=2×2=4 cm,
∴四边形APEB是矩形,∴PE=AB=6,BE=6,
∴EQ=BC﹣BE﹣CQ=16﹣6﹣4=6,
根据勾股定理得PQ=,
∴当t=2 s时,P,Q两点的距离为6 cm;
当t=4 s时,由运动知AP=3×4=12 cm,CQ=2×4=8cm,
∴四边形APEB是矩形,
∴PE=AB=6,BQ=8,CE=OP=4
∴EQ=BC﹣CE﹣BQ=16﹣4﹣8=4,
根据勾股定理得PQ=,
P,Q两点的距离为2cm.
(3)点Q从C点移动到B点所花的时间为16÷2=8s,
当点P在AO上时,S△POQ===12,
解得t=4.
当点P在OC上时,S△POQ===12,
解得t=6或﹣(舍弃).
当点P在CB上时,S△POQ===12,
解得t=18>8(不符合题意舍弃),
综上所述,经过4 s或6 s时,△POQ的面积为12 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
