空间向量及其应用复习课件
图片预览








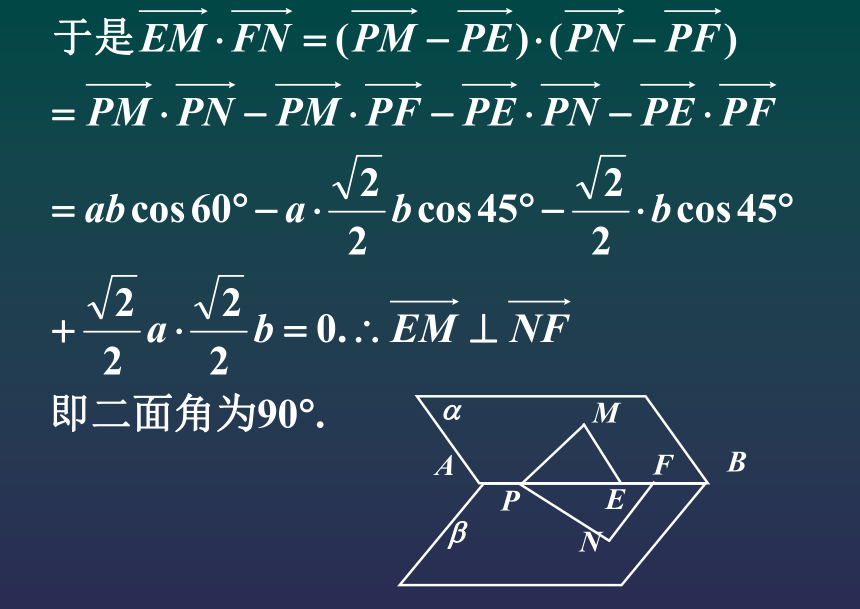

文档简介
课件78张PPT。第三章
空间向量与立体几何1.空间向量及其运算概念加法
减法
数乘
运算平面向量运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律加法交换律数乘分配律加法:三角形法则或
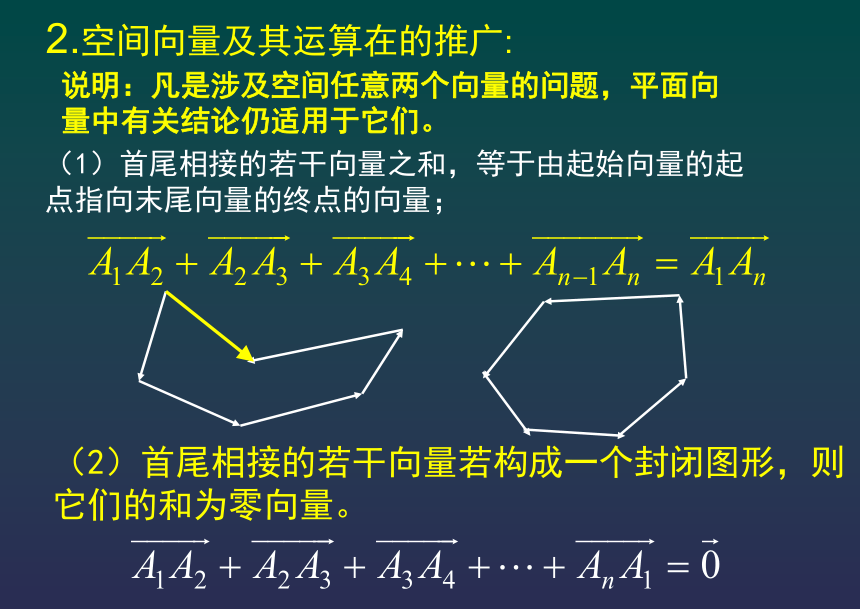
平行四边形法则减法:三角形法则数乘:ka,k为正数,负数,零加法结合律一、基本知识2.空间向量及其运算在的推广: (1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量;(2)首尾相接的若干向量若构成一个封闭图形,则它们的和为零向量。说明:凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们。(1)共线向量定理。
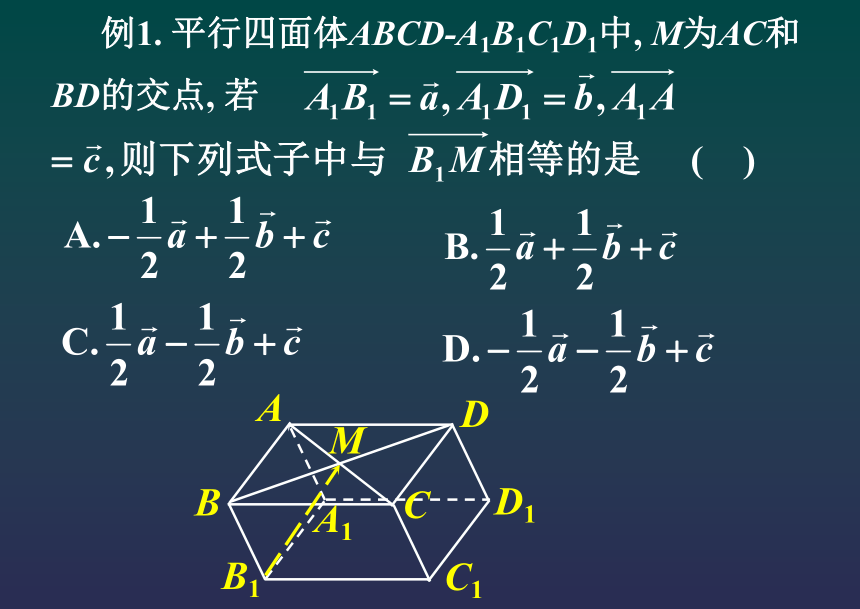
(2)共面向量定理。3.空间向量的两个定理 (1)(2)4.空间向量的数量积5.空间向量数量积的性质6.空间向量的基本定理是什么? 例1. 平行四面体ABCD-A1B1C1D1中, M为AC和BD的交点, 若 ABB1MCDC1A1D1[解析] 如图, 2. P是二面角?-AB-? 棱上的一点, 分别在?、? 平面上引射线PM、PN, 如果∠MPN=60?, ∠MPF=45? ∠NPF=45?那么二面角?-AB-? 的大小为( ) A. 30? B. 60? C. 90? D. 120?ABFENPM?? 2. P是二面角?-AB-? 棱上的一点, 分别在?、? 平面上引射线PM、PN, 如果∠MPN=60?, 那么二面角?-AB-? 的大小为( ) A. 30? B. 60? C. 90? D. 120?[解析] 如图, 设PM=a, PN=b, 作ME⊥AB, ∠EPM=∠EPN=45?,ABFENPM??ABFENPM??3.3.[证明][评注] [例3]余弦值的大小。4.[解析][例4]5.[解析][评注] 本题蕴涵着转化思想,即把空间垂直关系的判定、二面角的求解以及待定值的探求全部转化为平面向量的基本运算,给人耳目一新、思路清晰之感,确实为解决立体几何问题开拓了一条全新的思路.第二课时:空间向量的坐标运算及应用7、空间直角坐标系8、空间向量运算的坐标表示(一) 一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标. 空间向量坐标运算法则,关键是注意空间几何关系与向量坐标关系的转化,为此在利用向量的坐标运算判断空间几何关系时,首先要选定单位正交基,进而确定各向量的坐标。8、空间向量运算的坐标表示(二)练习1.设 分别是直线l1,l2的方向向量,根据下列条件,判断l1,l2的位置关系.平行垂直平行2、如何例用空间向量解决立体几何问题? 形到向量1、研究立体几何问题的常用三种方法:传统几何法、一般向量法、坐标向量法二、空间向量在解立体几何问题中的应用用l上一个定点A和l的一个方向向量
来确定3、用空间向量表示空间中的几何元素用其位置向量 来确定空间中的点P:空间中的任意一条直线l:(3)空间中的任意一个平面 :3、用空间向量表示空间中的几何元素通过 上一个定点O和两个向量 和 来确定空间中的任意一个平面 :(1)(4)(2)通过 上一个定点O和一个向量 来确定如图(4),直线 l ⊥ ,取直线l的方向向量 ,
则向量 叫做平面 的法向量3、用空间向量表示空间中的几何元素 设 分别是平面α,β的法向量,根据下
列条件,判断α,β的位置关系.垂直平行相交3、用空间向量表示立体几何中的位置关系练习体会4、怎样求一个平面的法向量? (0,1,0)(2)4、如何通过空间向量的运算,研究相应元素
之间的关系?线线平行、线面平行、面面平行线线垂直、线面垂直、面面垂直线线夹角、线面夹角、面面夹角回顾立几中有关概念平行关系 垂直关系角的关系距离关系点点距离、点线距离、点面距离
线线距离、线面距离、面面距离问题Ⅰ平行关系线线平行
线面平行
面面平行l∥ml∥αα∥β 设不重合的两直线l,m的方向向量分别为 ,
平面α,β的法向量分别为 ,则???OK?问题Ⅱ垂直关系线线垂直
线面垂直
面面垂直 设不重合的两直线l,m的方向向量分别为 ,
平面α,β的法向量分别为 ,则问题Ⅲ夹角关系线线夹角
线面夹角
面面夹角 设不重合的两直线l,m的方向向量分别为 ,
平面α,β的法向量分别为 ,则??问题Ⅳ 距离关系 设不重合的两直线l,m的方向向量分别为 ,
平面α,β的法向量分别为 ,则线面距离
面面距离点点距离直接利用空间中两点间距离公式求之点线距离已知点A与直线上任一点B组成的向量在直线法向量 方向上的射影的长度点面距离已知点A与平面上任一点B组成的向量在平面法向量 方向上的射影的长度线线距离已知在两直线上各任取点A、点B组成的向量在两直线公垂线的方向向量 上的射影的长度由平行的性质直接转化为点面距离来求解![考点搜索] 1. 理解空间向量坐标的概念,掌握空间向量的坐标运算. 2. 掌握用直角坐标计算空间向量数量积公式,掌握空间两点间的距离公式. 3. 掌握用空间向量坐标证明有关垂线和平行问题. 4. 利用空间向量坐标计算空间角和距离.[链接高考][例1][解析]P[例2]CA1B1C1D1ABDMNP[例2]CA1B1C1D1ABDMxyzN[解析][评注] 证明线面垂直,本质上就是证明线线垂直,而利用空间向量的坐标运算证明线线垂直,只要证明两直线上的向量的数量积为0即可.[例3]A1EB1C1BCADF[解析]A1EB1C1BCADFzyx[例4][解析][评注] 本题除考查概念是否清楚、公式记忆是否准确、运算是否熟练外,突出的是考查同学们运用向量研究空间图形的数学思想方法是否明确.1. 如图,正方体ABCD-A1B1C1D1中,EF是异面直线A1D与AC的公垂线段. 则AF= ( )[解析] 如图建立空间直角坐标系, 设正方形边长为1, 则A(1, 0, 0), C(0, 1, 0), A1(1, 0, 1), D(0, 0, 0).答案:B [解析] 设AB与平面xOz的交点为C(x, 0, z), 则 2. 已知两点A(1,?2,3), B(2,1,?1), 则AB连线与平面xOz的交点坐标是______.
空间向量与立体几何1.空间向量及其运算概念加法
减法
数乘
运算平面向量运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律加法交换律数乘分配律加法:三角形法则或
平行四边形法则减法:三角形法则数乘:ka,k为正数,负数,零加法结合律一、基本知识2.空间向量及其运算在的推广: (1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量;(2)首尾相接的若干向量若构成一个封闭图形,则它们的和为零向量。说明:凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们。(1)共线向量定理。
(2)共面向量定理。3.空间向量的两个定理 (1)(2)4.空间向量的数量积5.空间向量数量积的性质6.空间向量的基本定理是什么? 例1. 平行四面体ABCD-A1B1C1D1中, M为AC和BD的交点, 若 ABB1MCDC1A1D1[解析] 如图, 2. P是二面角?-AB-? 棱上的一点, 分别在?、? 平面上引射线PM、PN, 如果∠MPN=60?, ∠MPF=45? ∠NPF=45?那么二面角?-AB-? 的大小为( ) A. 30? B. 60? C. 90? D. 120?ABFENPM?? 2. P是二面角?-AB-? 棱上的一点, 分别在?、? 平面上引射线PM、PN, 如果∠MPN=60?, 那么二面角?-AB-? 的大小为( ) A. 30? B. 60? C. 90? D. 120?[解析] 如图, 设PM=a, PN=b, 作ME⊥AB, ∠EPM=∠EPN=45?,ABFENPM??ABFENPM??3.3.[证明][评注] [例3]余弦值的大小。4.[解析][例4]5.[解析][评注] 本题蕴涵着转化思想,即把空间垂直关系的判定、二面角的求解以及待定值的探求全部转化为平面向量的基本运算,给人耳目一新、思路清晰之感,确实为解决立体几何问题开拓了一条全新的思路.第二课时:空间向量的坐标运算及应用7、空间直角坐标系8、空间向量运算的坐标表示(一) 一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标. 空间向量坐标运算法则,关键是注意空间几何关系与向量坐标关系的转化,为此在利用向量的坐标运算判断空间几何关系时,首先要选定单位正交基,进而确定各向量的坐标。8、空间向量运算的坐标表示(二)练习1.设 分别是直线l1,l2的方向向量,根据下列条件,判断l1,l2的位置关系.平行垂直平行2、如何例用空间向量解决立体几何问题? 形到向量1、研究立体几何问题的常用三种方法:传统几何法、一般向量法、坐标向量法二、空间向量在解立体几何问题中的应用用l上一个定点A和l的一个方向向量
来确定3、用空间向量表示空间中的几何元素用其位置向量 来确定空间中的点P:空间中的任意一条直线l:(3)空间中的任意一个平面 :3、用空间向量表示空间中的几何元素通过 上一个定点O和两个向量 和 来确定空间中的任意一个平面 :(1)(4)(2)通过 上一个定点O和一个向量 来确定如图(4),直线 l ⊥ ,取直线l的方向向量 ,
则向量 叫做平面 的法向量3、用空间向量表示空间中的几何元素 设 分别是平面α,β的法向量,根据下
列条件,判断α,β的位置关系.垂直平行相交3、用空间向量表示立体几何中的位置关系练习体会4、怎样求一个平面的法向量? (0,1,0)(2)4、如何通过空间向量的运算,研究相应元素
之间的关系?线线平行、线面平行、面面平行线线垂直、线面垂直、面面垂直线线夹角、线面夹角、面面夹角回顾立几中有关概念平行关系 垂直关系角的关系距离关系点点距离、点线距离、点面距离
线线距离、线面距离、面面距离问题Ⅰ平行关系线线平行
线面平行
面面平行l∥ml∥αα∥β 设不重合的两直线l,m的方向向量分别为 ,
平面α,β的法向量分别为 ,则???OK?问题Ⅱ垂直关系线线垂直
线面垂直
面面垂直 设不重合的两直线l,m的方向向量分别为 ,
平面α,β的法向量分别为 ,则问题Ⅲ夹角关系线线夹角
线面夹角
面面夹角 设不重合的两直线l,m的方向向量分别为 ,
平面α,β的法向量分别为 ,则??问题Ⅳ 距离关系 设不重合的两直线l,m的方向向量分别为 ,
平面α,β的法向量分别为 ,则线面距离
面面距离点点距离直接利用空间中两点间距离公式求之点线距离已知点A与直线上任一点B组成的向量在直线法向量 方向上的射影的长度点面距离已知点A与平面上任一点B组成的向量在平面法向量 方向上的射影的长度线线距离已知在两直线上各任取点A、点B组成的向量在两直线公垂线的方向向量 上的射影的长度由平行的性质直接转化为点面距离来求解![考点搜索] 1. 理解空间向量坐标的概念,掌握空间向量的坐标运算. 2. 掌握用直角坐标计算空间向量数量积公式,掌握空间两点间的距离公式. 3. 掌握用空间向量坐标证明有关垂线和平行问题. 4. 利用空间向量坐标计算空间角和距离.[链接高考][例1][解析]P[例2]CA1B1C1D1ABDMNP[例2]CA1B1C1D1ABDMxyzN[解析][评注] 证明线面垂直,本质上就是证明线线垂直,而利用空间向量的坐标运算证明线线垂直,只要证明两直线上的向量的数量积为0即可.[例3]A1EB1C1BCADF[解析]A1EB1C1BCADFzyx[例4][解析][评注] 本题除考查概念是否清楚、公式记忆是否准确、运算是否熟练外,突出的是考查同学们运用向量研究空间图形的数学思想方法是否明确.1. 如图,正方体ABCD-A1B1C1D1中,EF是异面直线A1D与AC的公垂线段. 则AF= ( )[解析] 如图建立空间直角坐标系, 设正方形边长为1, 则A(1, 0, 0), C(0, 1, 0), A1(1, 0, 1), D(0, 0, 0).答案:B [解析] 设AB与平面xOz的交点为C(x, 0, z), 则 2. 已知两点A(1,?2,3), B(2,1,?1), 则AB连线与平面xOz的交点坐标是______.
