2.6.1 有理数的乘法与除法 课件(共30张PPT)七年级数学上册 苏科版
文档属性
| 名称 | 2.6.1 有理数的乘法与除法 课件(共30张PPT)七年级数学上册 苏科版 |  | |
| 格式 | pptx | ||
| 文件大小 | 43.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 08:44:59 | ||
图片预览










文档简介
第2章有理数
2.6.1 有理数的乘法
与除法
教学目标
贴近生活实例去感受有理数的乘法
理解有理数的乘法法则
能灵活运用有理数的乘法法则进行运算
有理数的乘法
——两数相乘
1、在水文观测中常遇到水位的上升与下降问题,请根据日常生活经验填写下面的空格。
(1)如果水位每天上升4cm,
那么3天后的水位比今天_______cm,
那么3天前的水位比今天_______cm;
(2)如果水位每天下降4cm,
那么3天后的水位比今天_______cm,
那么3天前的水位比今天_______cm。
2、将上述实例建立数学模型
——规定水位上升为正,水位下降为负,几天后为正,几天前为负。
(1)若水位上升4cm,记作“+4”,3天后,记作“+3”,
则3天后的水位变化量是“(+4)×(+3)”cm
即(+4)×(+3)=+12
(2)若水位上升4cm,记作“+4”,3天前,记作“-3”,
则3天前的水位变化量是“(+4)×(-3)”cm
即(+4)×(-3)=-12
(3)若水位下降4cm,记作“-4”,3天后,记作“+3”,
则3天前的水位变化量是“(-4)×(+3)”cm
即(-4)×(+3)=-12
(4)若水位下降4cm,记作“-4”,3天前,记作“-3”,
则3天前的水位变化量是“(-4)×(-3)”cm
即(-4)×(-3)=+12
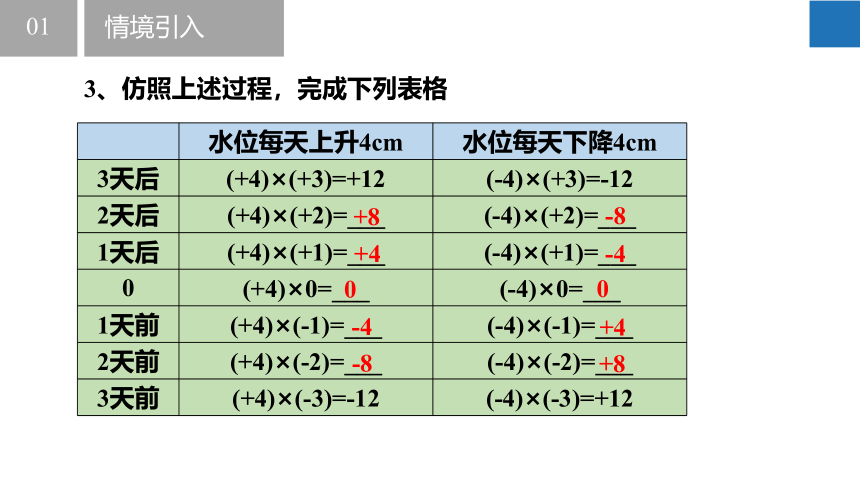
3、仿照上述过程,完成下列表格
水位每天上升4cm 水位每天下降4cm
3天后 (+4)×(+3)=+12 (-4)×(+3)=-12
2天后 (+4)×(+2)=___ (-4)×(+2)=___
1天后 (+4)×(+1)=___ (-4)×(+1)=___
0 (+4)×0=___ (-4)×0=___
1天前 (+4)×(-1)=___ (-4)×(-1)=___
2天前 (+4)×(-2)=___ (-4)×(-2)=___
3天前 (+4)×(-3)=-12 (-4)×(-3)=+12
4-1、根据算式,完成下列填空:
______两数相乘(选填:“同号”或“异号”),
结果的符号为______(选填:“正”或“负”),
符号后的数值为两乘数的______相乘。
(+4)×(+3)=+12
(+4)×(+2)=+8
(+4)×(+1)=+4
(-4)×(-1)=+4
(-4)×(-2)=+8
(-4)×(-3)=+12
4-2、根据算式,完成下列填空:
______两数相乘(选填:“同号”或“异号”),
结果的符号为______(选填:“正”或“负”),
符号后的数值为两乘数的______相乘。
(-4)×(+3)=-12
(-4)×(+2)=-8
(-4)×(+1)=-4
(+4)×(-1)=-4
(+4)×(-2)=-8
(+4)×(-3)=-12
4-3、根据算式,完成下列填空:
任何数与0相乘,都得_______。
(+4)×0=0 (-4)×0=0
两个不等于0的数相乘
一、定号—同号得正,异号得负;
二、定值—并把绝对值相乘。
任何数与0相乘,都得0。
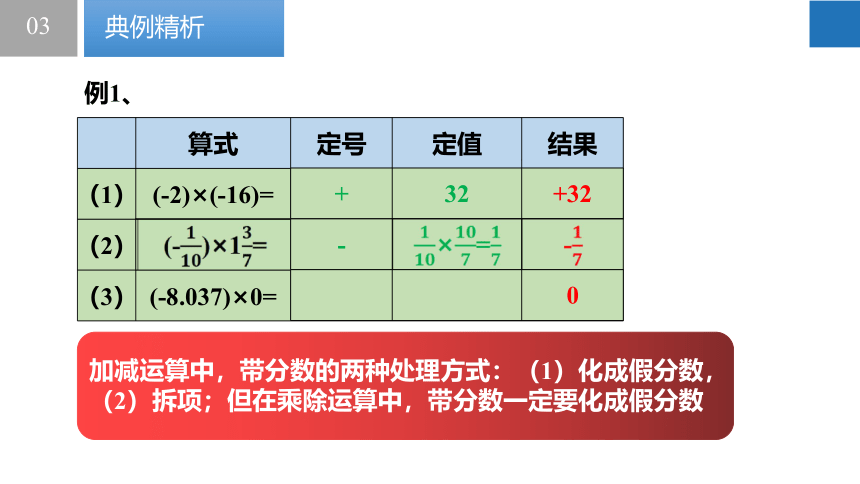
算式 定号 定值 结果
(1) (-2)×(-16)=
(2)
(3) (-8.037)×0=
加减运算中,带分数的两种处理方式:(1)化成假分数,(2)拆项;但在乘除运算中,带分数一定要化成假分数
有理数的乘法
——多数相乘
算一算,找规律
(+1)×(-2)=
(+1)×(-2)×(-3)=
(+1)×(-2)×(-3)×(-4)=
(+1)×(-2)×(-3)×(-4)×(-5)=
…
(+1)×(-2)×0×(-3)×(-4)×(-5)×…=
几个不等于0的数相乘,
当负因数有奇数个时,积为负;
当负因数有偶数个时,积为正。
几个数相乘,有一个因数为0,积就为0。
多个不等于0的数相乘,
一、定号—
当负因数有奇数个时,积为负,
当负因数有偶数个时,积为正;
二、定值—并把绝对值相乘。
多个数相乘,有一个因数为0,积就为0。
口诀:奇负偶正
例1、判断下列说法是否正确,正确打“?”,错误的打“?”
(1)两数之积为正,这两数同正
(2)两数之积为负,这两数异号
(3)几个数相乘,积的符号由负因数的个数决定
(4)三数相乘,积为负,这三个数都是负数
(3)×,应改成“几个不等于0的数相乘”
算式 定号 定值 结果
(1) (-3)×0×(-8)×2.5=
(2)
(3)
在乘除运算中,带分数一定要化成假分数
算式 定号 定值 结果
(4)
(5)
在乘除运算中,小数一定要化成分数
乘法运算律
情境引入
1-1:黑板上两个算式的结果相等吗?
1-2:把△、○中的数换成其他有理数,结果仍然相等吗?
相等,eg:(-5)×3=-15=3×(-5),(-2)×(-7)=14=(-7)×(-2),……
相等,eg:[(-5)×3]×2=-30=(-5)×(3×2),
[(-2)×(-7)]×3=42=(-2)×[(-7)×3],……
相等,eg:[(-5)+3]×2=-4=(-5)×2+3×2,
[(-2)+(-7)]×7=-63=(-2)×7+(-7)×7,……
乘法运算律
交换律:a×b=b×a
结合律:(a×b)×c=a×(b×c)
分配律:(a+b)×c=a×c+b×c
eg:(1)(-16)×(+2)×(-1/16)
=+(16×2×1/16)
=+(16×1/16×2)
=2
(2)(5/12-7/8)×24
=5/12×24-7/8×24
=10-21
=-11
eg:(3)-12×(1/4-2/3+1/6)
=(-12)×1/4+(-12)×(-2/3)+(-12)×1/6
=-3+8+(-2)
=3
eg:(4)9×(-5)+(-111)×(-5)-(-2)×(-5)
=(-5)×[9+(-111)-(-2)]
=(-5)×[9+(-111)-(-2)]
=(-5)×(-100)
=500
乘法分配律的逆用:
a×c+b×c=(a+b)×c
逆用关键:取相同,合不同
例1、(-8)×(-0.25)×(+125)×4
解:原式
=+(8×1/4×125×4)
=+(8×125)×(1/4×4)
=1000
交换律、结合律同时使用
例2、-6×(-3/2-2/3+5/6-2)
解:原式
=(-6)×(-3/2)+(-6)×(-2/3)+(-6)×(5/6)+(-6)×(-2)
=9+4+(-5)+12
=20
例3、1/4×(-51/2)+1/4×(-3.5)+1/4×2
解:原式
=1/4×[(-51/2)+(-3.5)+2]
=1/4×(-9+2)
=-7/4
两个不等于0的数相乘
一、定号—同号得正,异号得负;
二、定值—并把绝对值相乘。
任何数与0相乘,都得0。
乘法运算律
交换律:a×b=b×a
结合律:(a×b)×c=a×(b×c)
分配律:(a+b)×c=a×c+b×c
分配律的逆用:a×c+b×c=(a+b)×c
多个不等于0的数相乘,
一、定号—
当负因数有奇数个时,积为负,
当负因数有偶数个时,积为正;
二、定值—并把绝对值相乘。
多个数相乘,有一个因数为0,积就为0。
2.6.1 有理数的乘法
与除法
教学目标
贴近生活实例去感受有理数的乘法
理解有理数的乘法法则
能灵活运用有理数的乘法法则进行运算
有理数的乘法
——两数相乘
1、在水文观测中常遇到水位的上升与下降问题,请根据日常生活经验填写下面的空格。
(1)如果水位每天上升4cm,
那么3天后的水位比今天_______cm,
那么3天前的水位比今天_______cm;
(2)如果水位每天下降4cm,
那么3天后的水位比今天_______cm,
那么3天前的水位比今天_______cm。
2、将上述实例建立数学模型
——规定水位上升为正,水位下降为负,几天后为正,几天前为负。
(1)若水位上升4cm,记作“+4”,3天后,记作“+3”,
则3天后的水位变化量是“(+4)×(+3)”cm
即(+4)×(+3)=+12
(2)若水位上升4cm,记作“+4”,3天前,记作“-3”,
则3天前的水位变化量是“(+4)×(-3)”cm
即(+4)×(-3)=-12
(3)若水位下降4cm,记作“-4”,3天后,记作“+3”,
则3天前的水位变化量是“(-4)×(+3)”cm
即(-4)×(+3)=-12
(4)若水位下降4cm,记作“-4”,3天前,记作“-3”,
则3天前的水位变化量是“(-4)×(-3)”cm
即(-4)×(-3)=+12
3、仿照上述过程,完成下列表格
水位每天上升4cm 水位每天下降4cm
3天后 (+4)×(+3)=+12 (-4)×(+3)=-12
2天后 (+4)×(+2)=___ (-4)×(+2)=___
1天后 (+4)×(+1)=___ (-4)×(+1)=___
0 (+4)×0=___ (-4)×0=___
1天前 (+4)×(-1)=___ (-4)×(-1)=___
2天前 (+4)×(-2)=___ (-4)×(-2)=___
3天前 (+4)×(-3)=-12 (-4)×(-3)=+12
4-1、根据算式,完成下列填空:
______两数相乘(选填:“同号”或“异号”),
结果的符号为______(选填:“正”或“负”),
符号后的数值为两乘数的______相乘。
(+4)×(+3)=+12
(+4)×(+2)=+8
(+4)×(+1)=+4
(-4)×(-1)=+4
(-4)×(-2)=+8
(-4)×(-3)=+12
4-2、根据算式,完成下列填空:
______两数相乘(选填:“同号”或“异号”),
结果的符号为______(选填:“正”或“负”),
符号后的数值为两乘数的______相乘。
(-4)×(+3)=-12
(-4)×(+2)=-8
(-4)×(+1)=-4
(+4)×(-1)=-4
(+4)×(-2)=-8
(+4)×(-3)=-12
4-3、根据算式,完成下列填空:
任何数与0相乘,都得_______。
(+4)×0=0 (-4)×0=0
两个不等于0的数相乘
一、定号—同号得正,异号得负;
二、定值—并把绝对值相乘。
任何数与0相乘,都得0。
算式 定号 定值 结果
(1) (-2)×(-16)=
(2)
(3) (-8.037)×0=
加减运算中,带分数的两种处理方式:(1)化成假分数,(2)拆项;但在乘除运算中,带分数一定要化成假分数
有理数的乘法
——多数相乘
算一算,找规律
(+1)×(-2)=
(+1)×(-2)×(-3)=
(+1)×(-2)×(-3)×(-4)=
(+1)×(-2)×(-3)×(-4)×(-5)=
…
(+1)×(-2)×0×(-3)×(-4)×(-5)×…=
几个不等于0的数相乘,
当负因数有奇数个时,积为负;
当负因数有偶数个时,积为正。
几个数相乘,有一个因数为0,积就为0。
多个不等于0的数相乘,
一、定号—
当负因数有奇数个时,积为负,
当负因数有偶数个时,积为正;
二、定值—并把绝对值相乘。
多个数相乘,有一个因数为0,积就为0。
口诀:奇负偶正
例1、判断下列说法是否正确,正确打“?”,错误的打“?”
(1)两数之积为正,这两数同正
(2)两数之积为负,这两数异号
(3)几个数相乘,积的符号由负因数的个数决定
(4)三数相乘,积为负,这三个数都是负数
(3)×,应改成“几个不等于0的数相乘”
算式 定号 定值 结果
(1) (-3)×0×(-8)×2.5=
(2)
(3)
在乘除运算中,带分数一定要化成假分数
算式 定号 定值 结果
(4)
(5)
在乘除运算中,小数一定要化成分数
乘法运算律
情境引入
1-1:黑板上两个算式的结果相等吗?
1-2:把△、○中的数换成其他有理数,结果仍然相等吗?
相等,eg:(-5)×3=-15=3×(-5),(-2)×(-7)=14=(-7)×(-2),……
相等,eg:[(-5)×3]×2=-30=(-5)×(3×2),
[(-2)×(-7)]×3=42=(-2)×[(-7)×3],……
相等,eg:[(-5)+3]×2=-4=(-5)×2+3×2,
[(-2)+(-7)]×7=-63=(-2)×7+(-7)×7,……
乘法运算律
交换律:a×b=b×a
结合律:(a×b)×c=a×(b×c)
分配律:(a+b)×c=a×c+b×c
eg:(1)(-16)×(+2)×(-1/16)
=+(16×2×1/16)
=+(16×1/16×2)
=2
(2)(5/12-7/8)×24
=5/12×24-7/8×24
=10-21
=-11
eg:(3)-12×(1/4-2/3+1/6)
=(-12)×1/4+(-12)×(-2/3)+(-12)×1/6
=-3+8+(-2)
=3
eg:(4)9×(-5)+(-111)×(-5)-(-2)×(-5)
=(-5)×[9+(-111)-(-2)]
=(-5)×[9+(-111)-(-2)]
=(-5)×(-100)
=500
乘法分配律的逆用:
a×c+b×c=(a+b)×c
逆用关键:取相同,合不同
例1、(-8)×(-0.25)×(+125)×4
解:原式
=+(8×1/4×125×4)
=+(8×125)×(1/4×4)
=1000
交换律、结合律同时使用
例2、-6×(-3/2-2/3+5/6-2)
解:原式
=(-6)×(-3/2)+(-6)×(-2/3)+(-6)×(5/6)+(-6)×(-2)
=9+4+(-5)+12
=20
例3、1/4×(-51/2)+1/4×(-3.5)+1/4×2
解:原式
=1/4×[(-51/2)+(-3.5)+2]
=1/4×(-9+2)
=-7/4
两个不等于0的数相乘
一、定号—同号得正,异号得负;
二、定值—并把绝对值相乘。
任何数与0相乘,都得0。
乘法运算律
交换律:a×b=b×a
结合律:(a×b)×c=a×(b×c)
分配律:(a+b)×c=a×c+b×c
分配律的逆用:a×c+b×c=(a+b)×c
多个不等于0的数相乘,
一、定号—
当负因数有奇数个时,积为负,
当负因数有偶数个时,积为正;
二、定值—并把绝对值相乘。
多个数相乘,有一个因数为0,积就为0。
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
