北京市2022-2023学年期末试题汇编-平行四边形、三角形的周长与面积、用方格计算面积(含答案)五年级上册数学人教版
文档属性
| 名称 | 北京市2022-2023学年期末试题汇编-平行四边形、三角形的周长与面积、用方格计算面积(含答案)五年级上册数学人教版 |

|
|
| 格式 | doc | ||
| 文件大小 | 877.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-20 19:32:10 | ||
图片预览


文档简介
北京市2022-2023学年期末试题汇编-平行四边形、三角形的周长与面积、用方格计算面积(试题)-五年级上册数学人教版
一.选择题(共9小题)
1.(2022秋 石景山区期末)如图。比较图中图形①、②、③的面积,可以得出( )
A.①的面积最小 B.②的面积最小
C.③的面积最小 D.无法确定
2.(2022秋 朝阳区期末)如图,如果把一个长5cm,宽3cm的长方形拉成一个平行四边形,这个平行四边形的高可能是( )cm。
A.2 B.3 C.4 D.5
3.(2022秋 石景山区期末)一个直角三角形的三条边分别为6cm、8cm、10cm,这个三角形的面积是( )平方厘米。
A.48 B.40 C.30 D.24
4.(2022秋 西城区期末)如图直角三角形的面积是( )cm2。
A.6 B.10 C.12 D.15
5.(2022秋 朝阳区期末)在一组平行线间有一些图形(如图)。与左侧三角形面积相等的是( )
A.① B.② C.③ D.④
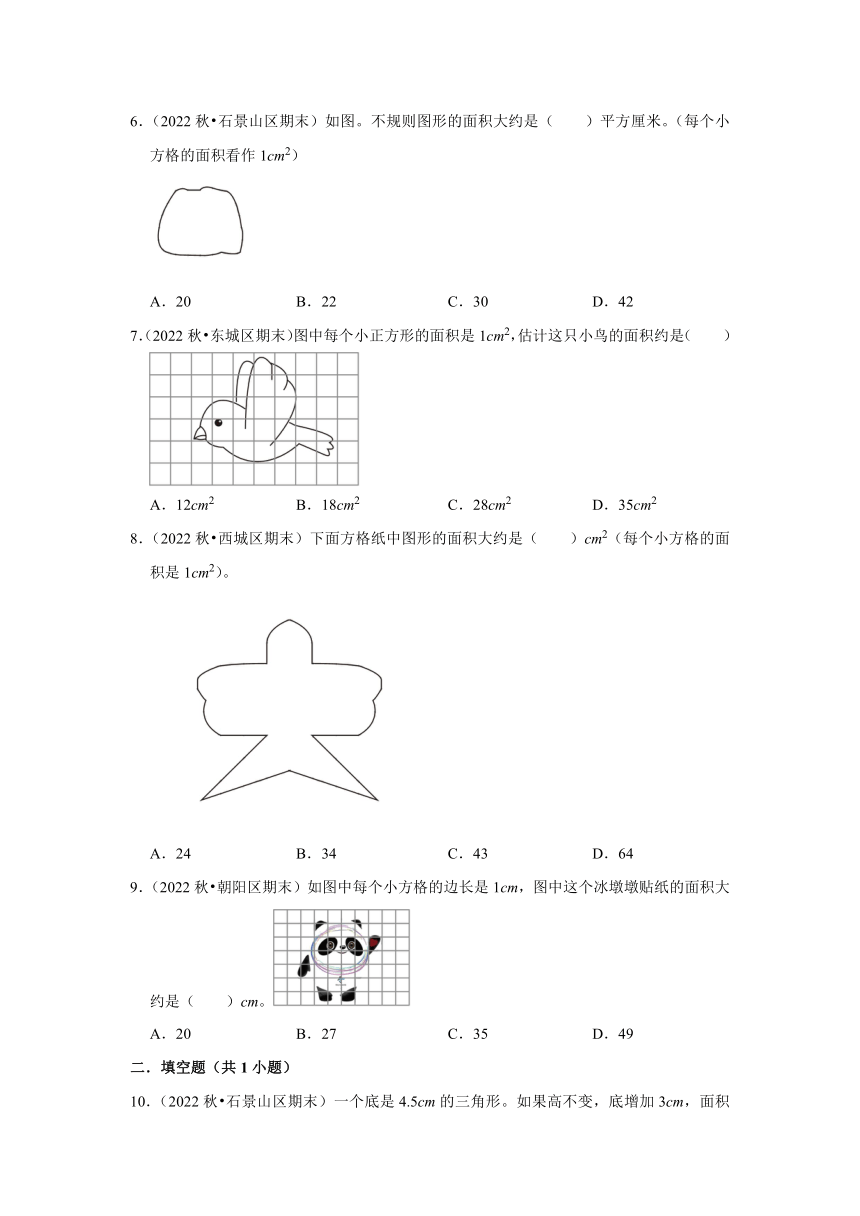
6.(2022秋 石景山区期末)如图。不规则图形的面积大约是( )平方厘米。(每个小方格的面积看作1cm2)
A.20 B.22 C.30 D.42
7.(2022秋 东城区期末)图中每个小正方形的面积是1cm2,估计这只小鸟的面积约是( )
A.12cm2 B.18cm2 C.28cm2 D.35cm2
8.(2022秋 西城区期末)下面方格纸中图形的面积大约是( )cm2(每个小方格的面积是1cm2)。
A.24 B.34 C.43 D.64
9.(2022秋 朝阳区期末)如图中每个小方格的边长是1cm,图中这个冰墩墩贴纸的面积大约是( )cm。
A.20 B.27 C.35 D.49
二.填空题(共1小题)
10.(2022秋 石景山区期末)一个底是4.5cm的三角形。如果高不变,底增加3cm,面积就增加6cm2。原来三角形的面积是 平方厘米。
三.操作题(共2小题)
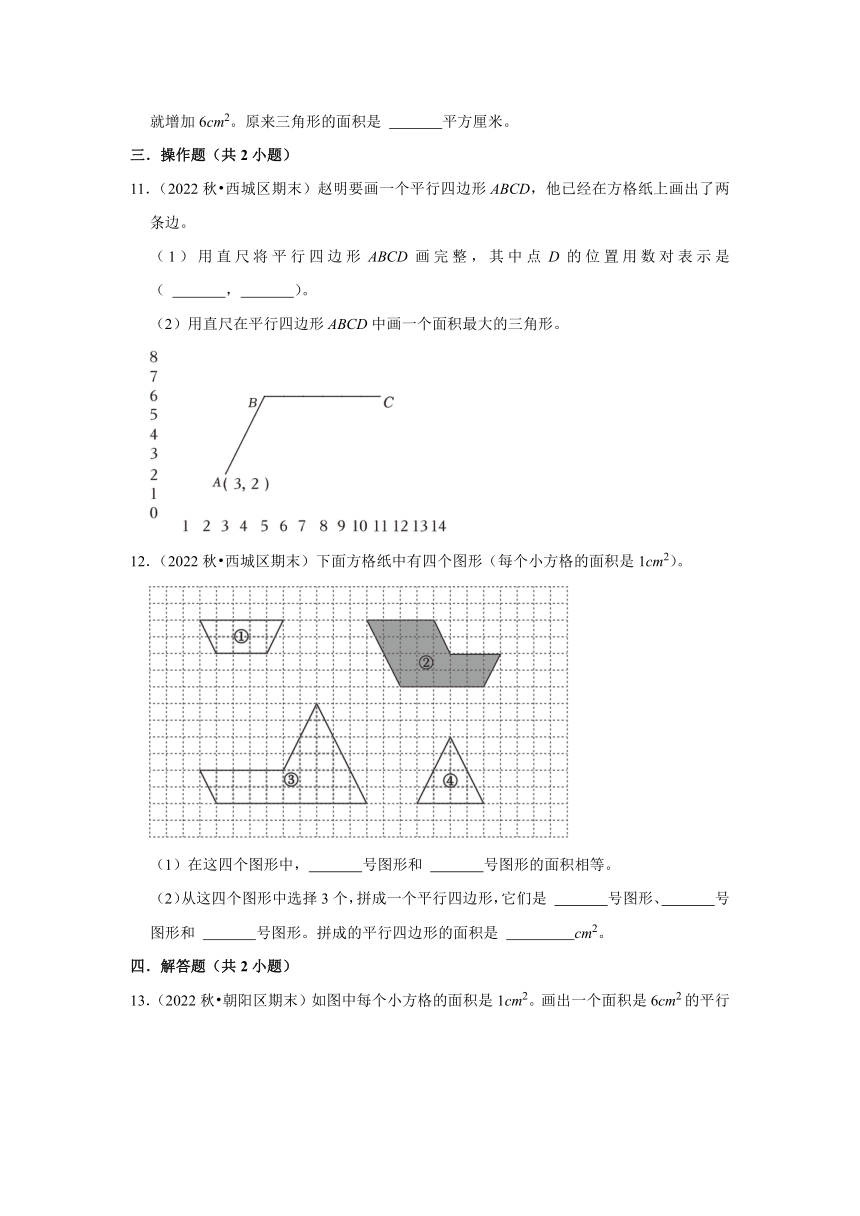
11.(2022秋 西城区期末)赵明要画一个平行四边形ABCD,他已经在方格纸上画出了两条边。
(1)用直尺将平行四边形ABCD画完整,其中点D的位置用数对表示是( , )。
(2)用直尺在平行四边形ABCD中画一个面积最大的三角形。
12.(2022秋 西城区期末)下面方格纸中有四个图形(每个小方格的面积是1cm2)。
(1)在这四个图形中, 号图形和 号图形的面积相等。
(2)从这四个图形中选择3个,拼成一个平行四边形,它们是 号图形、 号图形和 号图形。拼成的平行四边形的面积是 cm2。
四.解答题(共2小题)
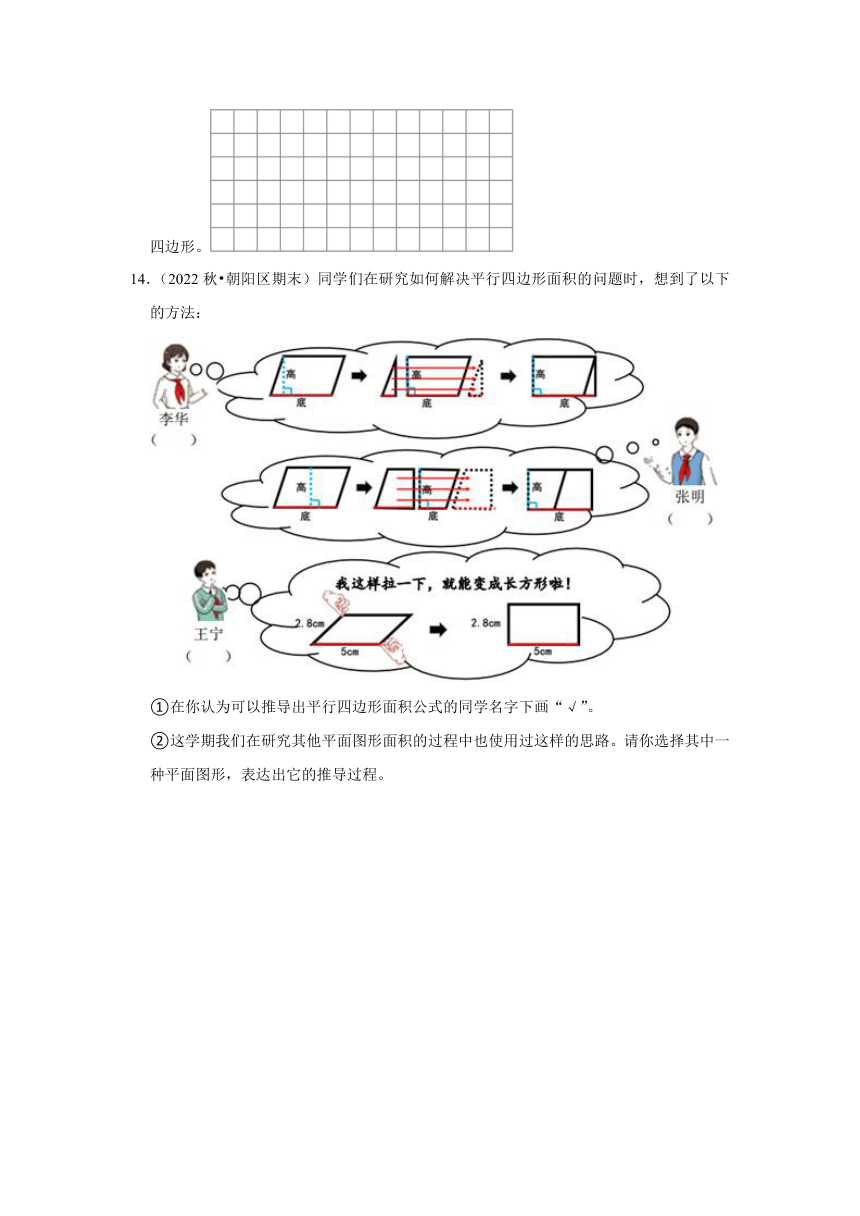
13.(2022秋 朝阳区期末)如图中每个小方格的面积是1cm2。画出一个面积是6cm2的平行四边形。
14.(2022秋 朝阳区期末)同学们在研究如何解决平行四边形面积的问题时,想到了以下的方法:
①在你认为可以推导出平行四边形面积公式的同学名字下画“√”。
②这学期我们在研究其他平面图形面积的过程中也使用过这样的思路。请你选择其中一种平面图形,表达出它的推导过程。
北京市2022-2023学年期末试题汇编-平行四边形、三角形的周长与面积、用方格计算面积(试题)-五年级上册数学人教版
参考答案与试题解析
一.选择题(共9小题)
1.(2022秋 石景山区期末)如图。比较图中图形①、②、③的面积,可以得出( )
A.①的面积最小 B.②的面积最小
C.③的面积最小 D.无法确定
【答案】A
【解答】解:设三个图形的高都是h,则:
三角形的面积=18h÷2=9h;
平行四边形的面积=12h;
梯形的面积=(6+14)h÷2=10h;
12h>10h>9h
所以①的面积最小。
故选:A。
2.(2022秋 朝阳区期末)如图,如果把一个长5cm,宽3cm的长方形拉成一个平行四边形,这个平行四边形的高可能是( )cm。
A.2 B.3 C.4 D.5
【答案】A
【解答】解:由图可知:
长方形拉成一个平行四边形后,底没变,但是高变小了,平行四边形的高小于长方形的宽,小于3厘米,所以只有2厘米符合。
故选:A。
3.(2022秋 石景山区期末)一个直角三角形的三条边分别为6cm、8cm、10cm,这个三角形的面积是( )平方厘米。
A.48 B.40 C.30 D.24
【答案】D
【解答】解:8×6÷2
=48÷2
=24(平方厘米)
答:这个三角形的面积是24平方厘米。
故选:D。
4.(2022秋 西城区期末)如图直角三角形的面积是( )cm2。
A.6 B.10 C.12 D.15
【答案】A
【解答】解:4×3÷2
=12÷2
=6(cm2)
答:直角三角形的面积是6cm2。
故选:A.
5.(2022秋 朝阳区期末)在一组平行线间有一些图形(如图)。与左侧三角形面积相等的是( )
A.① B.② C.③ D.④
【答案】D
【解答】解:因为夹在两平行线之间的距离相等,所以这几个图形的高是相等的,可设为hcm,
左侧三角形面积是hcm2,
①的面积是1.5hcm2,
②的面积是2hcm2,
③的面积大于是2hcm2,
④的面积是hcm2。
故选:D。
6.(2022秋 石景山区期末)如图。不规则图形的面积大约是( )平方厘米。(每个小方格的面积看作1cm2)
A.20 B.22 C.30 D.42
【答案】C
【解答】解:(5+7)×5÷2
=12×5÷2
=30(平方厘米)
答:不规则图形的面积大约是30平方厘米。
故选:C。
7.(2022秋 东城区期末)图中每个小正方形的面积是1cm2,估计这只小鸟的面积约是( )
A.12cm2 B.18cm2 C.28cm2 D.35cm2
【答案】A
【解答】解:满格的5个,不满格的有18个。
5+18÷2
=5+9
=14(个)
14×1=14(平方厘米)
14平方厘米接近选项中的A。
故选:A。
8.(2022秋 西城区期末)下面方格纸中图形的面积大约是( )cm2(每个小方格的面积是1cm2)。
A.24 B.34 C.43 D.64
【答案】B
【解答】解:24+20÷2
=24+10
=34(平方厘米)
答:方格纸中图形的面积大约是34cm2。
故选:B。
9.(2022秋 朝阳区期末)如图中每个小方格的边长是1cm,图中这个冰墩墩贴纸的面积大约是( )cm。
A.20 B.27 C.35 D.49
【答案】B
【解答】解:整格的大约有19格,半格大约有16格,也就是16÷2=8(格),19加8合起来大约是27格。
故选:B。
二.填空题(共1小题)
10.(2022秋 石景山区期末)一个底是4.5cm的三角形。如果高不变,底增加3cm,面积就增加6cm2。原来三角形的面积是 9 平方厘米。
【答案】9。
【解答】解:6×2÷3
=12÷3
=4(厘米)
4.5×4÷2
=18÷2
=9(平方厘米)
答:原来三角形的面积是9平方厘米。
故答案为:9。
三.操作题(共2小题)
11.(2022秋 西城区期末)赵明要画一个平行四边形ABCD,他已经在方格纸上画出了两条边。
(1)用直尺将平行四边形ABCD画完整,其中点D的位置用数对表示是( 9 , 2 )。
(2)用直尺在平行四边形ABCD中画一个面积最大的三角形。
【答案】9;2;。
【解答】解:(1)用直尺将平行四边形ABCD画完整,其中点D的位置用数对表示是( 9,2)。
(2)用直尺在平行四边形ABCD中画一个面积最大的三角形。
故答案为:9;2。
12.(2022秋 西城区期末)下面方格纸中有四个图形(每个小方格的面积是1cm2)。
(1)在这四个图形中, ① 号图形和 ④ 号图形的面积相等。
(2)从这四个图形中选择3个,拼成一个平行四边形,它们是 ① 号图形、 ② 号图形和 ③ 号图形。拼成的平行四边形的面积是 54 cm2。
【答案】(1)①,④;(2)①,②,③,54。
【解答】解:(1)①(3+5)×2÷2
=8×2÷2
=8(cm2)
②4×2+(5+7)×2÷2
=8+12×2÷2
=8+12
=20(cm2)
③9×2+4×4÷2
=18+8
=26(cm2)
④4×4÷2=8(cm2)
答:在这四个图形中,①号图形和④号图形的面积相等。
(2)8+20+26=54(cm2)
答:从这四个图形中选择3个,拼成一个平行四边形,它们是①号图形、②号图形和③号图形。拼成的平行四边形的面积是54cm2。
故答案为:①,④;①,②,③,54。
四.解答题(共2小题)
13.(2022秋 朝阳区期末)如图中每个小方格的面积是1cm2。画出一个面积是6cm2的平行四边形。
【答案】(答案不唯一)。
【解答】解:如图所示(答案不唯一):
14.(2022秋 朝阳区期末)同学们在研究如何解决平行四边形面积的问题时,想到了以下的方法:
①在你认为可以推导出平行四边形面积公式的同学名字下画“√”。
②这学期我们在研究其他平面图形面积的过程中也使用过这样的思路。请你选择其中一种平面图形,表达出它的推导过程。
【答案】①
②如图:
根据两个完全相同的三角形可以拼成一个平行四边形,把两个完全一样的三角形重合,把其中一个旋转180°,再平移可拼成一个平行四边形,这个平行四边形的底等于三角形的底,高等于三角形的高,所以三角形的面积是和它等底等高的三角形面积的一半,据此解答。(答案不唯一)
【解答】解:①解答如下:
②如图:
根据两个完全相同的三角形可以拼成一个平行四边形,把两个完全一样的三角形重合,把其中一个旋转180°,再平移可拼成一个平行四边形,这个平行四边形的底等于三角形的底,高等于三角形的高,所以三角形的面积是和它等底等高的三角形面积的一半,据此解答。(答案不唯一)
一.选择题(共9小题)
1.(2022秋 石景山区期末)如图。比较图中图形①、②、③的面积,可以得出( )
A.①的面积最小 B.②的面积最小
C.③的面积最小 D.无法确定
2.(2022秋 朝阳区期末)如图,如果把一个长5cm,宽3cm的长方形拉成一个平行四边形,这个平行四边形的高可能是( )cm。
A.2 B.3 C.4 D.5
3.(2022秋 石景山区期末)一个直角三角形的三条边分别为6cm、8cm、10cm,这个三角形的面积是( )平方厘米。
A.48 B.40 C.30 D.24
4.(2022秋 西城区期末)如图直角三角形的面积是( )cm2。
A.6 B.10 C.12 D.15
5.(2022秋 朝阳区期末)在一组平行线间有一些图形(如图)。与左侧三角形面积相等的是( )
A.① B.② C.③ D.④
6.(2022秋 石景山区期末)如图。不规则图形的面积大约是( )平方厘米。(每个小方格的面积看作1cm2)
A.20 B.22 C.30 D.42
7.(2022秋 东城区期末)图中每个小正方形的面积是1cm2,估计这只小鸟的面积约是( )
A.12cm2 B.18cm2 C.28cm2 D.35cm2
8.(2022秋 西城区期末)下面方格纸中图形的面积大约是( )cm2(每个小方格的面积是1cm2)。
A.24 B.34 C.43 D.64
9.(2022秋 朝阳区期末)如图中每个小方格的边长是1cm,图中这个冰墩墩贴纸的面积大约是( )cm。
A.20 B.27 C.35 D.49
二.填空题(共1小题)
10.(2022秋 石景山区期末)一个底是4.5cm的三角形。如果高不变,底增加3cm,面积就增加6cm2。原来三角形的面积是 平方厘米。
三.操作题(共2小题)
11.(2022秋 西城区期末)赵明要画一个平行四边形ABCD,他已经在方格纸上画出了两条边。
(1)用直尺将平行四边形ABCD画完整,其中点D的位置用数对表示是( , )。
(2)用直尺在平行四边形ABCD中画一个面积最大的三角形。
12.(2022秋 西城区期末)下面方格纸中有四个图形(每个小方格的面积是1cm2)。
(1)在这四个图形中, 号图形和 号图形的面积相等。
(2)从这四个图形中选择3个,拼成一个平行四边形,它们是 号图形、 号图形和 号图形。拼成的平行四边形的面积是 cm2。
四.解答题(共2小题)
13.(2022秋 朝阳区期末)如图中每个小方格的面积是1cm2。画出一个面积是6cm2的平行四边形。
14.(2022秋 朝阳区期末)同学们在研究如何解决平行四边形面积的问题时,想到了以下的方法:
①在你认为可以推导出平行四边形面积公式的同学名字下画“√”。
②这学期我们在研究其他平面图形面积的过程中也使用过这样的思路。请你选择其中一种平面图形,表达出它的推导过程。
北京市2022-2023学年期末试题汇编-平行四边形、三角形的周长与面积、用方格计算面积(试题)-五年级上册数学人教版
参考答案与试题解析
一.选择题(共9小题)
1.(2022秋 石景山区期末)如图。比较图中图形①、②、③的面积,可以得出( )
A.①的面积最小 B.②的面积最小
C.③的面积最小 D.无法确定
【答案】A
【解答】解:设三个图形的高都是h,则:
三角形的面积=18h÷2=9h;
平行四边形的面积=12h;
梯形的面积=(6+14)h÷2=10h;
12h>10h>9h
所以①的面积最小。
故选:A。
2.(2022秋 朝阳区期末)如图,如果把一个长5cm,宽3cm的长方形拉成一个平行四边形,这个平行四边形的高可能是( )cm。
A.2 B.3 C.4 D.5
【答案】A
【解答】解:由图可知:
长方形拉成一个平行四边形后,底没变,但是高变小了,平行四边形的高小于长方形的宽,小于3厘米,所以只有2厘米符合。
故选:A。
3.(2022秋 石景山区期末)一个直角三角形的三条边分别为6cm、8cm、10cm,这个三角形的面积是( )平方厘米。
A.48 B.40 C.30 D.24
【答案】D
【解答】解:8×6÷2
=48÷2
=24(平方厘米)
答:这个三角形的面积是24平方厘米。
故选:D。
4.(2022秋 西城区期末)如图直角三角形的面积是( )cm2。
A.6 B.10 C.12 D.15
【答案】A
【解答】解:4×3÷2
=12÷2
=6(cm2)
答:直角三角形的面积是6cm2。
故选:A.
5.(2022秋 朝阳区期末)在一组平行线间有一些图形(如图)。与左侧三角形面积相等的是( )
A.① B.② C.③ D.④
【答案】D
【解答】解:因为夹在两平行线之间的距离相等,所以这几个图形的高是相等的,可设为hcm,
左侧三角形面积是hcm2,
①的面积是1.5hcm2,
②的面积是2hcm2,
③的面积大于是2hcm2,
④的面积是hcm2。
故选:D。
6.(2022秋 石景山区期末)如图。不规则图形的面积大约是( )平方厘米。(每个小方格的面积看作1cm2)
A.20 B.22 C.30 D.42
【答案】C
【解答】解:(5+7)×5÷2
=12×5÷2
=30(平方厘米)
答:不规则图形的面积大约是30平方厘米。
故选:C。
7.(2022秋 东城区期末)图中每个小正方形的面积是1cm2,估计这只小鸟的面积约是( )
A.12cm2 B.18cm2 C.28cm2 D.35cm2
【答案】A
【解答】解:满格的5个,不满格的有18个。
5+18÷2
=5+9
=14(个)
14×1=14(平方厘米)
14平方厘米接近选项中的A。
故选:A。
8.(2022秋 西城区期末)下面方格纸中图形的面积大约是( )cm2(每个小方格的面积是1cm2)。
A.24 B.34 C.43 D.64
【答案】B
【解答】解:24+20÷2
=24+10
=34(平方厘米)
答:方格纸中图形的面积大约是34cm2。
故选:B。
9.(2022秋 朝阳区期末)如图中每个小方格的边长是1cm,图中这个冰墩墩贴纸的面积大约是( )cm。
A.20 B.27 C.35 D.49
【答案】B
【解答】解:整格的大约有19格,半格大约有16格,也就是16÷2=8(格),19加8合起来大约是27格。
故选:B。
二.填空题(共1小题)
10.(2022秋 石景山区期末)一个底是4.5cm的三角形。如果高不变,底增加3cm,面积就增加6cm2。原来三角形的面积是 9 平方厘米。
【答案】9。
【解答】解:6×2÷3
=12÷3
=4(厘米)
4.5×4÷2
=18÷2
=9(平方厘米)
答:原来三角形的面积是9平方厘米。
故答案为:9。
三.操作题(共2小题)
11.(2022秋 西城区期末)赵明要画一个平行四边形ABCD,他已经在方格纸上画出了两条边。
(1)用直尺将平行四边形ABCD画完整,其中点D的位置用数对表示是( 9 , 2 )。
(2)用直尺在平行四边形ABCD中画一个面积最大的三角形。
【答案】9;2;。
【解答】解:(1)用直尺将平行四边形ABCD画完整,其中点D的位置用数对表示是( 9,2)。
(2)用直尺在平行四边形ABCD中画一个面积最大的三角形。
故答案为:9;2。
12.(2022秋 西城区期末)下面方格纸中有四个图形(每个小方格的面积是1cm2)。
(1)在这四个图形中, ① 号图形和 ④ 号图形的面积相等。
(2)从这四个图形中选择3个,拼成一个平行四边形,它们是 ① 号图形、 ② 号图形和 ③ 号图形。拼成的平行四边形的面积是 54 cm2。
【答案】(1)①,④;(2)①,②,③,54。
【解答】解:(1)①(3+5)×2÷2
=8×2÷2
=8(cm2)
②4×2+(5+7)×2÷2
=8+12×2÷2
=8+12
=20(cm2)
③9×2+4×4÷2
=18+8
=26(cm2)
④4×4÷2=8(cm2)
答:在这四个图形中,①号图形和④号图形的面积相等。
(2)8+20+26=54(cm2)
答:从这四个图形中选择3个,拼成一个平行四边形,它们是①号图形、②号图形和③号图形。拼成的平行四边形的面积是54cm2。
故答案为:①,④;①,②,③,54。
四.解答题(共2小题)
13.(2022秋 朝阳区期末)如图中每个小方格的面积是1cm2。画出一个面积是6cm2的平行四边形。
【答案】(答案不唯一)。
【解答】解:如图所示(答案不唯一):
14.(2022秋 朝阳区期末)同学们在研究如何解决平行四边形面积的问题时,想到了以下的方法:
①在你认为可以推导出平行四边形面积公式的同学名字下画“√”。
②这学期我们在研究其他平面图形面积的过程中也使用过这样的思路。请你选择其中一种平面图形,表达出它的推导过程。
【答案】①
②如图:
根据两个完全相同的三角形可以拼成一个平行四边形,把两个完全一样的三角形重合,把其中一个旋转180°,再平移可拼成一个平行四边形,这个平行四边形的底等于三角形的底,高等于三角形的高,所以三角形的面积是和它等底等高的三角形面积的一半,据此解答。(答案不唯一)
【解答】解:①解答如下:
②如图:
根据两个完全相同的三角形可以拼成一个平行四边形,把两个完全一样的三角形重合,把其中一个旋转180°,再平移可拼成一个平行四边形,这个平行四边形的底等于三角形的底,高等于三角形的高,所以三角形的面积是和它等底等高的三角形面积的一半,据此解答。(答案不唯一)
同课章节目录
