2023—2024学年苏科版数学七年级上册6.3余角、补角、对顶角(1)导学案(表格式 无答案)
文档属性
| 名称 | 2023—2024学年苏科版数学七年级上册6.3余角、补角、对顶角(1)导学案(表格式 无答案) | 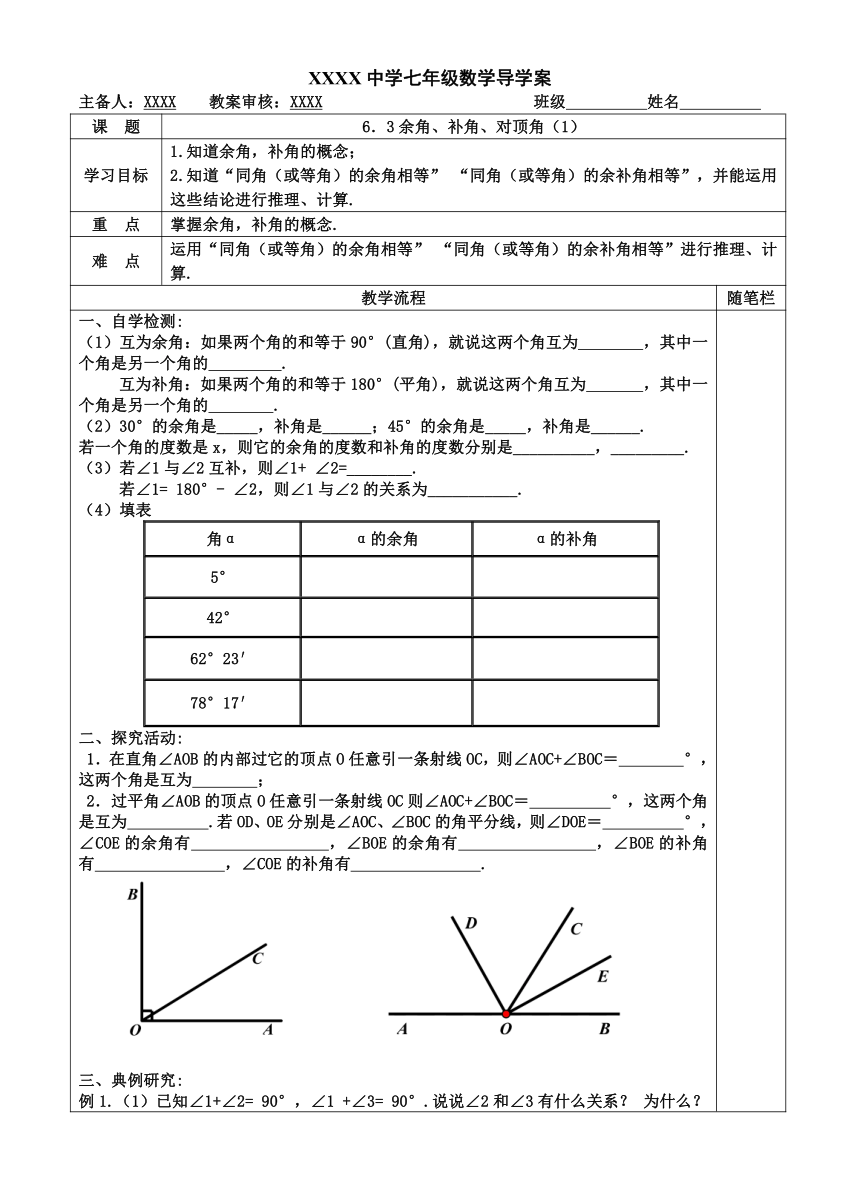 | |
| 格式 | docx | ||
| 文件大小 | 37.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-21 20:28:42 | ||
图片预览

文档简介
XXXX中学七年级数学导学案
主备人:XXXX 教案审核:XXXX 班级 姓名
课 题 6.3余角、补角、对顶角(1)
学习目标 1.知道余角,补角的概念; 2.知道“同角(或等角)的余角相等” “同角(或等角)的余补角相等”,并能运用这些结论进行推理、计算.
重 点 掌握余角,补角的概念.
难 点 运用“同角(或等角)的余角相等” “同角(或等角)的余补角相等”进行推理、计算.
教学流程 随笔栏
一、自学检测: (1)互为余角:如果两个角的和等于90°(直角),就说这两个角互为 ,其中一个角是另一个角的 . 互为补角:如果两个角的和等于180°(平角),就说这两个角互为 ,其中一个角是另一个角的 . (2)30°的余角是_____,补角是______;45°的余角是_____,补角是______. 若一个角的度数是x,则它的余角的度数和补角的度数分别是__________,_________. (3)若∠1与∠2互补,则∠1+ ∠2=________. 若∠1= 180°- ∠2,则∠1与∠2的关系为___________. (4)填表 角αα的余角α的补角5°42°62°23′78°17′
探究活动: 1.在直角∠AOB的内部过它的顶点O任意引一条射线OC,则∠AOC+∠BOC= °,这两个角是互为 ; 2.过平角∠AOB的顶点O任意引一条射线OC则∠AOC+∠BOC= °,这两个角是互为 .若OD、OE分别是∠AOC、∠BOC的角平分线,则∠DOE= °,∠COE的余角有 ,∠BOE的余角有 ,∠BOE的补角有 ,∠COE的补角有 . 三、典例研究: 例1.(1)已知∠1+∠2= 90°,∠1 +∠3= 90°.说说∠2和∠3有什么关系? 为什么? (2)如果∠1+∠2= 90°,∠3 +∠4= 90°.若∠1=∠3,那么∠2和∠4有什么关系? 例2.(1)已知∠1+∠2= 180°,∠1 +∠3= 180°.说说∠2和∠3有什么关系? 为什么? (2)如果∠1+∠2= 180°,∠3 +∠4= 180°.若∠1=∠3,那么∠2和∠4有什么关系? 小结:同角(或等角)的余角 ; 同角(或等角)的补角 . 课堂反馈: 1.几何语言的规范书写: ⑴∵和互余 ∴_____(或) ⑵∵和互补 ∴_____(或) 2.一个角是,则它的余角是_______,它的补角是_______. 3.,则它的余角等于_ ______;的补角是,则=_______. 4.若∠1+∠2=90°,∠3+∠2=90°,∠1=40°,则∠3=_____°,依据是_ __. 5.一个角比它的补角的度数少40°,则这个角的度数为 . 五、拓展提高 如图,∠AOC和∠BOD都是直角,∠DOC=28 ,求∠AOB的度数. D C A B O 六、我的收获
课堂反思
主备人:XXXX 教案审核:XXXX 班级 姓名
课 题 6.3余角、补角、对顶角(1)
学习目标 1.知道余角,补角的概念; 2.知道“同角(或等角)的余角相等” “同角(或等角)的余补角相等”,并能运用这些结论进行推理、计算.
重 点 掌握余角,补角的概念.
难 点 运用“同角(或等角)的余角相等” “同角(或等角)的余补角相等”进行推理、计算.
教学流程 随笔栏
一、自学检测: (1)互为余角:如果两个角的和等于90°(直角),就说这两个角互为 ,其中一个角是另一个角的 . 互为补角:如果两个角的和等于180°(平角),就说这两个角互为 ,其中一个角是另一个角的 . (2)30°的余角是_____,补角是______;45°的余角是_____,补角是______. 若一个角的度数是x,则它的余角的度数和补角的度数分别是__________,_________. (3)若∠1与∠2互补,则∠1+ ∠2=________. 若∠1= 180°- ∠2,则∠1与∠2的关系为___________. (4)填表 角αα的余角α的补角5°42°62°23′78°17′
探究活动: 1.在直角∠AOB的内部过它的顶点O任意引一条射线OC,则∠AOC+∠BOC= °,这两个角是互为 ; 2.过平角∠AOB的顶点O任意引一条射线OC则∠AOC+∠BOC= °,这两个角是互为 .若OD、OE分别是∠AOC、∠BOC的角平分线,则∠DOE= °,∠COE的余角有 ,∠BOE的余角有 ,∠BOE的补角有 ,∠COE的补角有 . 三、典例研究: 例1.(1)已知∠1+∠2= 90°,∠1 +∠3= 90°.说说∠2和∠3有什么关系? 为什么? (2)如果∠1+∠2= 90°,∠3 +∠4= 90°.若∠1=∠3,那么∠2和∠4有什么关系? 例2.(1)已知∠1+∠2= 180°,∠1 +∠3= 180°.说说∠2和∠3有什么关系? 为什么? (2)如果∠1+∠2= 180°,∠3 +∠4= 180°.若∠1=∠3,那么∠2和∠4有什么关系? 小结:同角(或等角)的余角 ; 同角(或等角)的补角 . 课堂反馈: 1.几何语言的规范书写: ⑴∵和互余 ∴_____(或) ⑵∵和互补 ∴_____(或) 2.一个角是,则它的余角是_______,它的补角是_______. 3.,则它的余角等于_ ______;的补角是,则=_______. 4.若∠1+∠2=90°,∠3+∠2=90°,∠1=40°,则∠3=_____°,依据是_ __. 5.一个角比它的补角的度数少40°,则这个角的度数为 . 五、拓展提高 如图,∠AOC和∠BOD都是直角,∠DOC=28 ,求∠AOB的度数. D C A B O 六、我的收获
课堂反思
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
