2023-2024学年苏科版八年级数学上册第二章轴对称图形 复习题(含答案)
文档属性
| 名称 | 2023-2024学年苏科版八年级数学上册第二章轴对称图形 复习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 217.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-21 20:37:32 | ||
图片预览

文档简介
初二第一学期数学复习《轴对称图形》
满分:100分 时间:90分钟
一、选择题 (每题3分,共24分)
1.下列图案是轴对称图形的是 ( )
2.在△ABC中,若∠B,∠C平分线的交点P恰好在BC边的高AD上,则△ABC一定是 ( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
3.如图所示的是一台球桌面的示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是 ( )
A.① B.② C.⑤ D.⑥
4.如图,已知点P到AE,AD,BC的距离相等,有下列说法:①点P在∠BAC的平分线上;②点P在∠CBE的平分线上;③点P在∠BCD的平分线上;④点P在∠BAC,∠CBE,∠BCD的平分线的交点上.其中正确的是 ( )
A.①②③④ B.①②③ C.④ D.②③
5.如图,在△ABC中,AB=AC,∠A=50°,P是△ABC内一点,且∠PBC=∠PCA,则∠BPC的度数等于 ( )
A.100° B.115° C.130° D.140°
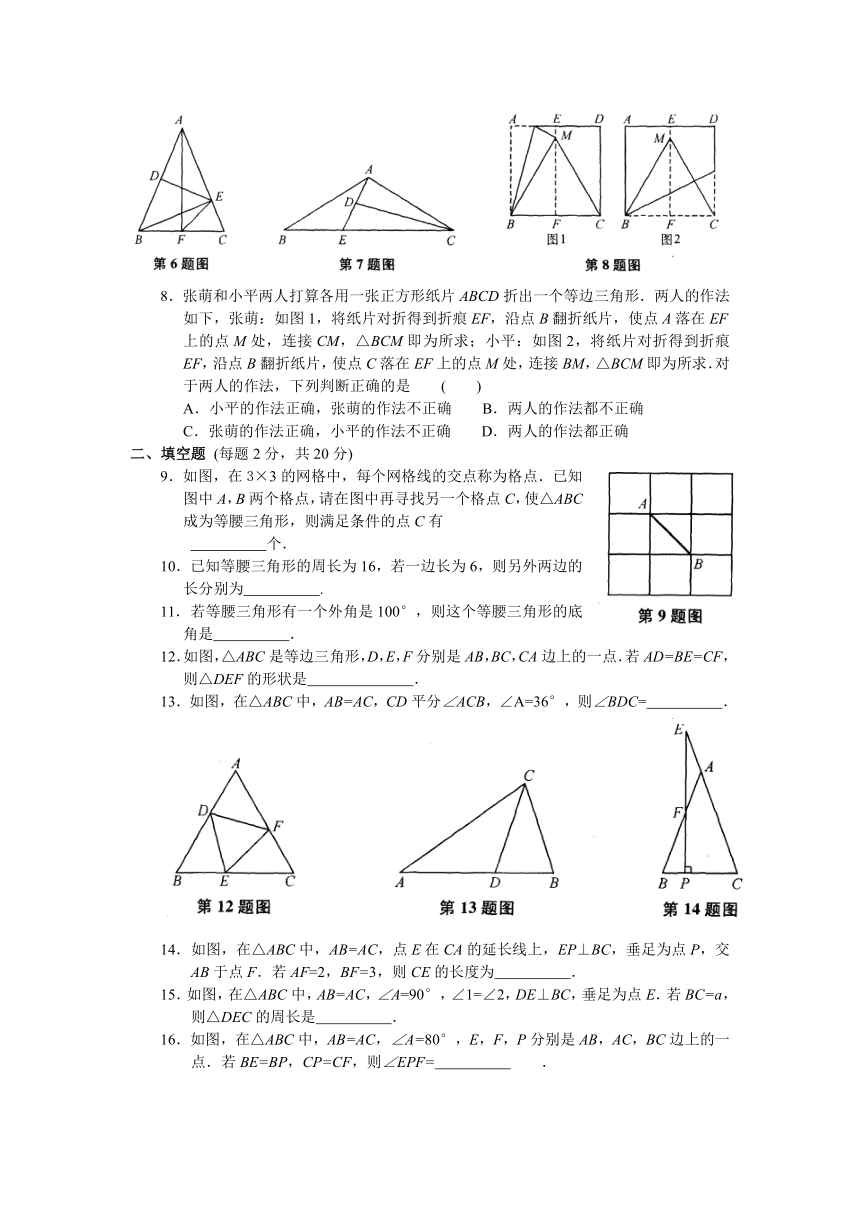
6.如图,在△ABC中,AB=AC,DE垂直平分AB,BE⊥AC。AF⊥BC,则下列结论错误的是 ( )
A.BF=EF B.DE=EF C.∠EFC=45° D.∠BEF=∠CBE
7.如图,D为△ABC内一点,CD平分∠ACB,AE⊥CD,垂足为点D,交BC于点E,∠B=∠BAE,若BC=5,AC=3,则AD的长为 ( )
A 1 B.1.5 C.2 D.2.5
8.张萌和小平两人打算各用一张正方形纸片ABCD折出一个等边三角形.两人的作法如下,张萌:如图1,将纸片对折得到折痕EF,沿点B翻折纸片,使点A落在EF上的点M处,连接CM,△BCM即为所求;小平:如图2,将纸片对折得到折痕EF,沿点B翻折纸片,使点C落在EF上的点M处,连接BM,△BCM即为所求.对于两人的作法,下列判断正确的是 ( )
A.小平的作法正确,张萌的作法不正确 B.两人的作法都不正确
C.张萌的作法正确,小平的作法不正确 D.两人的作法都正确
二、填空题 (每题2分,共20分)
9.如图,在3×3的网格中,每个网格线的交点称为格点.已知图中A,B两个格点,请在图中再寻找另一个格点C,使△ABC成为等腰三角形,则满足条件的点C有
个.
10.已知等腰三角形的周长为16,若一边长为6,则另外两边的长分别为 .
11.若等腰三角形有一个外角是100°,则这个等腰三角形的底角是 .
12.如图,△ABC是等边三角形,D,E,F分别是AB,BC,CA边上的一点.若AD=BE=CF,则△DEF的形状是 .
13.如图,在△ABC中,AB=AC,CD平分∠ACB,∠A=36°,则∠BDC= .
14.如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为点P,交AB于点F.若AF=2,BF=3,则CE的长度为 .
15.如图,在△ABC中,AB=AC,∠A=90°,∠1=∠2,DE⊥BC,垂足为点E.若BC=a,则△DEC的周长是 .
16.如图,在△ABC中,AB=AC,∠A=80°,E,F,P分别是AB,AC,BC边上的一点.若BE=BP,CP=CF,则∠EPF= .
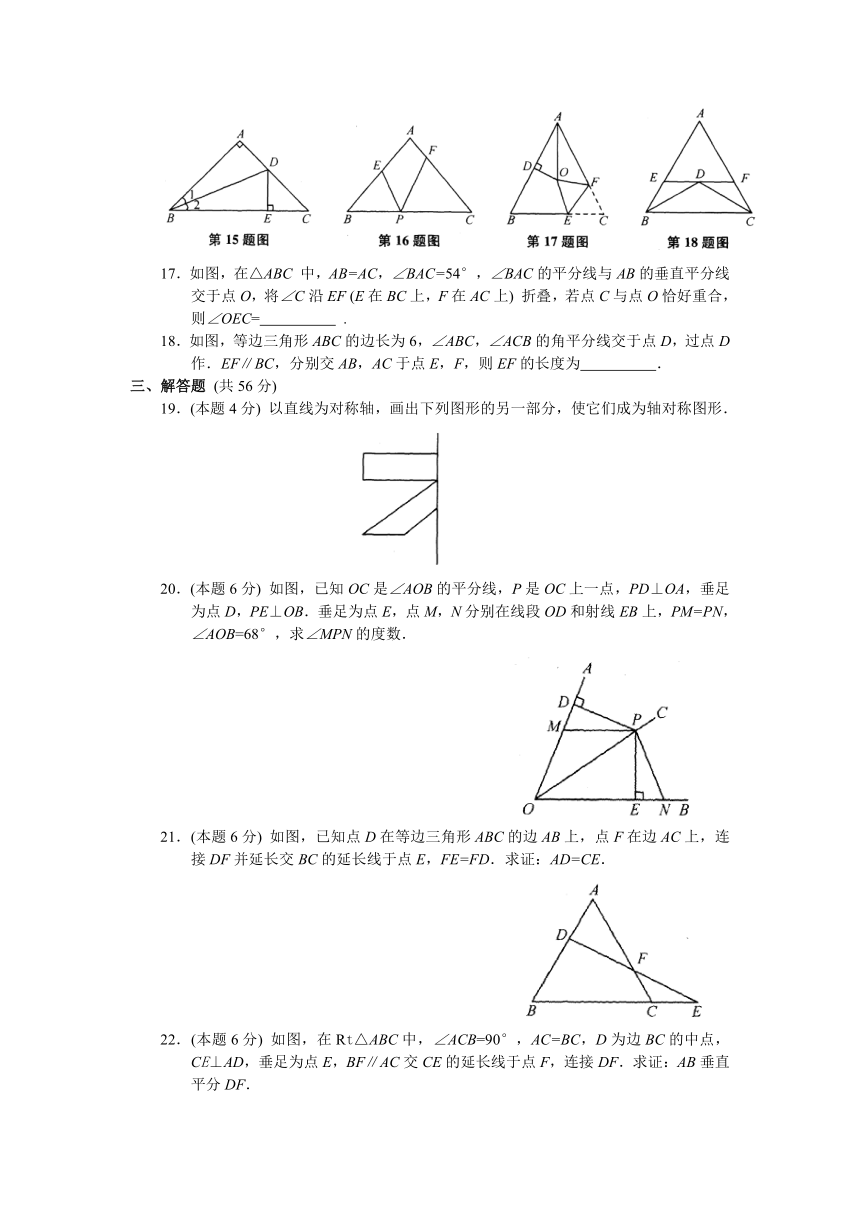
17.如图,在△ABC 中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF (E在BC上,F在AC上) 折叠,若点C与点O恰好重合,则∠OEC= .
18.如图,等边三角形ABC的边长为6,∠ABC,∠ACB的角平分线交于点D,过点D作.EF∥BC,分别交AB,AC于点E,F,则EF的长度为 .
三、解答题 (共56分)
19.(本题4分) 以直线为对称轴,画出下列图形的另一部分,使它们成为轴对称图形.
20.(本题6分) 如图,已知OC是∠AOB的平分线,P是OC上一点,PD⊥OA,垂足为点D,PE⊥OB.垂足为点E,点M,N分别在线段OD和射线EB上,PM=PN,∠AOB=68°,求∠MPN的度数.
21.(本题6分) 如图,已知点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,FE=FD.求证:AD=CE.
22.(本题6分) 如图,在Rt△ABC中,∠ACB=90°,AC=BC,D为边BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F,连接DF.求证:AB垂直平分DF.
23.(本题8分) 如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1) △AEF≌△CEB;(2) AF=2CD.
24.(本题8分) 如图,已知△ABC为等边三角形,延长BC到点D,延长BA到点E,并且使AE=BD.连接CE,DE.求证:EC=ED.
25.(本题8分) 如图,∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.
26.(本题10分)
(1) 如图1,点C是线段AB上一点,分别以AC,BC为边在AB的同侧作等边三角形ACM和等边三角形CBN,连接AN,BM.分别取BM,AN的中点E,F,连接CE,CF,EF.观察并猜想△CEF的形状,并说明理由.
(2) 若将 (1) 中的“以AC,BC为边在AB的同侧作等边三角形ACM和等边三角形CBN”改为“以AC,BC为腰在AB的同侧作等腰三角形ACM和等腰三角形CBN,且∠ACM=∠BCN≠60°”,其他条件不变,如图2所示,那么 (1) 中的结论还成立吗 若成立,请加以证明;若不成立,请说明坪南.
参考答案
一、选择题
1.D 2.C 3.A 4.A 5.B 6.B 7.A 8.D
二、填空题
9.8 10.5,5或6,4 11.80°或50° 12.等边三角形 13.72° 14.7 15.a 16.50° 17.108°(提示:连接OB,OC,可求得∠OCE=∠COE=36°,进而求得∠OEC=108°) 18.4 (提示:根据BD和CD分别平分∠ABC 和∠ACB,EF∥BC,可求出BE=DE,DF=FC,进一步证明△AEF是等边三角形,则EF=2BE=AC,即EF△AB=4)
三、解答题
19.如图所示的图形即为所求作的图形
20.∵ OC平分∠AOB,PD⊥OA,PE⊥OB,垂足分别为点D,E,∴ PD=PE.在Rt△MPD与Rt△NPE中,∵ PM=PN,PD=PE.∴ Rt△MPD≌Rt△NPE,∴ ∠MPD=∠NPE.∵ ∠MPN=∠MPE+∠EPN,∴ ∠MPN=∠MPE+∠DPM=∠DPE.在四边形OEPD中,∠AOB=68°,∠ODP=90°.∠OEP=90°,∴ ∠DPE=112°,即∠MPN=112°
21.过点D作DG∥BC,∴ ∠ADG=∠B,又∵ FE=FD,∴ DG=CE.∵ △ABC为等边三角形,∴ ∠A=∠B=60°,∴ ∠A=∠ADG=60°,即△ADG为等边三角形,∴ AD=DG,∴ AD=CE
22.∵ ∠BCE+∠ACE=90°,∠ACE+∠CAD=90°,∴ ∠BCE=∠CAD.∵ BF∥AC,∴ BF⊥BC,∴ ∠ACD=∠CBF=90°.又∵ AC=CB,∴ △ACD≌△CBF,∴ CD=BF.∵ CD=BD=BC,∴ BF=BD,∴ △BFD为等腰直角三角形.∵ ∠ACB=90°,CA=CB,∴ ∠ABC=45°.∵ ∠FBD=90°,∴ ∠ABF=45°,∴ ∠ABC=∠ABF,即BA是∠FBD的平分线.又∵ BF=BD,∴ BA⊥DF,∴ AB垂直平分DF
23.(1) ∵ AD⊥BC,∴ ∠B+∠BAD=90°.∵ CE⊥AB,∴ ∠B+∠BCE=90°,∴ ∠EAF=∠ECB.在△AEF和△CEB中,∴ △AEF≌△CEB, (2) ∵ △AEF≌△CEB,∴ AF=BC.∵ AB=AC,AD⊥BC,∴ CD=BD,BC= 2CD, ∴ AF=2CD
24.延长BD至点F,使DF=BC,连接EF.∵ AE=BD,△ABC为等边三角形,∴ BE=BF,∠B=60°,∴ △BEF为等边三角形,∴ ∠F=60°.在△ECB和△EDF中,BE=EF,∠B=∠F=60°,BC=DF.∴ △ECB≌△EDF,∴ EC=ED
25.画图如下.OD,ON,DM之间的数量关系为:OD=ON+DM或ON=OD+DM.分三种情况,①如图1,线段OD,ON,DM之间的数量关系为:OD=ON+DM,理由如下:∵ OC是角平分线,∴ ∠AOC=∠BOC.∵ CD∥OB,∴ ∠CME=∠ONE,∠C=∠BOC=∠AOC,∴ OD=CD.在△CEM和△OEN中,∠C=∠BOC,∠CME=∠ONE,CE=OE,∴ △CEM≌△OEN,∴ ON=CM,∴OD=CD=CM+DM=ON+DM.②如图2,由①易得OD=ON+DM.③如图3,类似①可证得OD=CD,△CEM≌△OEN,得ON=CM=CD+DM=OD+DM
26.(1) △CEF是等边三角形.理由:∵ △ACM与△BCN是等边三角形,∴ CA=CM,CN=CB,∠ACM=∠BCN=60°,∴ ∠ACN=∠BCM=120°,∴ △CAN≌△CMB,∴ AN=BM,∠CAN=∠CMB.∵ E,F分别为BM,AN的中点,∴ AF=ME,∴ △ACF≌△MCE,∴ CE=CF,∠ACF=∠MCE.∵ ∠ACF=∠ACM+∠MCF,∴ ∠MCE=∠MCF+∠FCE,即∠ECF=∠ACM=60°,∴ △CEF是等边三角形 (2) 不成立,理由如下:方法同(1)可得△CAN≌△CMB,△ACF≌△MCE,∴CE=CF,∠ACF=∠MCE.∵ ∠ACF=∠ACM+∠MCF,∴ ∠MCE=∠MCF+∠FCE,即∠ECF=∠ACM≠60°,∴ △CEF是等腰三角形
满分:100分 时间:90分钟
一、选择题 (每题3分,共24分)
1.下列图案是轴对称图形的是 ( )
2.在△ABC中,若∠B,∠C平分线的交点P恰好在BC边的高AD上,则△ABC一定是 ( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
3.如图所示的是一台球桌面的示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是 ( )
A.① B.② C.⑤ D.⑥
4.如图,已知点P到AE,AD,BC的距离相等,有下列说法:①点P在∠BAC的平分线上;②点P在∠CBE的平分线上;③点P在∠BCD的平分线上;④点P在∠BAC,∠CBE,∠BCD的平分线的交点上.其中正确的是 ( )
A.①②③④ B.①②③ C.④ D.②③
5.如图,在△ABC中,AB=AC,∠A=50°,P是△ABC内一点,且∠PBC=∠PCA,则∠BPC的度数等于 ( )
A.100° B.115° C.130° D.140°
6.如图,在△ABC中,AB=AC,DE垂直平分AB,BE⊥AC。AF⊥BC,则下列结论错误的是 ( )
A.BF=EF B.DE=EF C.∠EFC=45° D.∠BEF=∠CBE
7.如图,D为△ABC内一点,CD平分∠ACB,AE⊥CD,垂足为点D,交BC于点E,∠B=∠BAE,若BC=5,AC=3,则AD的长为 ( )
A 1 B.1.5 C.2 D.2.5
8.张萌和小平两人打算各用一张正方形纸片ABCD折出一个等边三角形.两人的作法如下,张萌:如图1,将纸片对折得到折痕EF,沿点B翻折纸片,使点A落在EF上的点M处,连接CM,△BCM即为所求;小平:如图2,将纸片对折得到折痕EF,沿点B翻折纸片,使点C落在EF上的点M处,连接BM,△BCM即为所求.对于两人的作法,下列判断正确的是 ( )
A.小平的作法正确,张萌的作法不正确 B.两人的作法都不正确
C.张萌的作法正确,小平的作法不正确 D.两人的作法都正确
二、填空题 (每题2分,共20分)
9.如图,在3×3的网格中,每个网格线的交点称为格点.已知图中A,B两个格点,请在图中再寻找另一个格点C,使△ABC成为等腰三角形,则满足条件的点C有
个.
10.已知等腰三角形的周长为16,若一边长为6,则另外两边的长分别为 .
11.若等腰三角形有一个外角是100°,则这个等腰三角形的底角是 .
12.如图,△ABC是等边三角形,D,E,F分别是AB,BC,CA边上的一点.若AD=BE=CF,则△DEF的形状是 .
13.如图,在△ABC中,AB=AC,CD平分∠ACB,∠A=36°,则∠BDC= .
14.如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为点P,交AB于点F.若AF=2,BF=3,则CE的长度为 .
15.如图,在△ABC中,AB=AC,∠A=90°,∠1=∠2,DE⊥BC,垂足为点E.若BC=a,则△DEC的周长是 .
16.如图,在△ABC中,AB=AC,∠A=80°,E,F,P分别是AB,AC,BC边上的一点.若BE=BP,CP=CF,则∠EPF= .
17.如图,在△ABC 中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF (E在BC上,F在AC上) 折叠,若点C与点O恰好重合,则∠OEC= .
18.如图,等边三角形ABC的边长为6,∠ABC,∠ACB的角平分线交于点D,过点D作.EF∥BC,分别交AB,AC于点E,F,则EF的长度为 .
三、解答题 (共56分)
19.(本题4分) 以直线为对称轴,画出下列图形的另一部分,使它们成为轴对称图形.
20.(本题6分) 如图,已知OC是∠AOB的平分线,P是OC上一点,PD⊥OA,垂足为点D,PE⊥OB.垂足为点E,点M,N分别在线段OD和射线EB上,PM=PN,∠AOB=68°,求∠MPN的度数.
21.(本题6分) 如图,已知点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,FE=FD.求证:AD=CE.
22.(本题6分) 如图,在Rt△ABC中,∠ACB=90°,AC=BC,D为边BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F,连接DF.求证:AB垂直平分DF.
23.(本题8分) 如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1) △AEF≌△CEB;(2) AF=2CD.
24.(本题8分) 如图,已知△ABC为等边三角形,延长BC到点D,延长BA到点E,并且使AE=BD.连接CE,DE.求证:EC=ED.
25.(本题8分) 如图,∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.
26.(本题10分)
(1) 如图1,点C是线段AB上一点,分别以AC,BC为边在AB的同侧作等边三角形ACM和等边三角形CBN,连接AN,BM.分别取BM,AN的中点E,F,连接CE,CF,EF.观察并猜想△CEF的形状,并说明理由.
(2) 若将 (1) 中的“以AC,BC为边在AB的同侧作等边三角形ACM和等边三角形CBN”改为“以AC,BC为腰在AB的同侧作等腰三角形ACM和等腰三角形CBN,且∠ACM=∠BCN≠60°”,其他条件不变,如图2所示,那么 (1) 中的结论还成立吗 若成立,请加以证明;若不成立,请说明坪南.
参考答案
一、选择题
1.D 2.C 3.A 4.A 5.B 6.B 7.A 8.D
二、填空题
9.8 10.5,5或6,4 11.80°或50° 12.等边三角形 13.72° 14.7 15.a 16.50° 17.108°(提示:连接OB,OC,可求得∠OCE=∠COE=36°,进而求得∠OEC=108°) 18.4 (提示:根据BD和CD分别平分∠ABC 和∠ACB,EF∥BC,可求出BE=DE,DF=FC,进一步证明△AEF是等边三角形,则EF=2BE=AC,即EF△AB=4)
三、解答题
19.如图所示的图形即为所求作的图形
20.∵ OC平分∠AOB,PD⊥OA,PE⊥OB,垂足分别为点D,E,∴ PD=PE.在Rt△MPD与Rt△NPE中,∵ PM=PN,PD=PE.∴ Rt△MPD≌Rt△NPE,∴ ∠MPD=∠NPE.∵ ∠MPN=∠MPE+∠EPN,∴ ∠MPN=∠MPE+∠DPM=∠DPE.在四边形OEPD中,∠AOB=68°,∠ODP=90°.∠OEP=90°,∴ ∠DPE=112°,即∠MPN=112°
21.过点D作DG∥BC,∴ ∠ADG=∠B,又∵ FE=FD,∴ DG=CE.∵ △ABC为等边三角形,∴ ∠A=∠B=60°,∴ ∠A=∠ADG=60°,即△ADG为等边三角形,∴ AD=DG,∴ AD=CE
22.∵ ∠BCE+∠ACE=90°,∠ACE+∠CAD=90°,∴ ∠BCE=∠CAD.∵ BF∥AC,∴ BF⊥BC,∴ ∠ACD=∠CBF=90°.又∵ AC=CB,∴ △ACD≌△CBF,∴ CD=BF.∵ CD=BD=BC,∴ BF=BD,∴ △BFD为等腰直角三角形.∵ ∠ACB=90°,CA=CB,∴ ∠ABC=45°.∵ ∠FBD=90°,∴ ∠ABF=45°,∴ ∠ABC=∠ABF,即BA是∠FBD的平分线.又∵ BF=BD,∴ BA⊥DF,∴ AB垂直平分DF
23.(1) ∵ AD⊥BC,∴ ∠B+∠BAD=90°.∵ CE⊥AB,∴ ∠B+∠BCE=90°,∴ ∠EAF=∠ECB.在△AEF和△CEB中,∴ △AEF≌△CEB, (2) ∵ △AEF≌△CEB,∴ AF=BC.∵ AB=AC,AD⊥BC,∴ CD=BD,BC= 2CD, ∴ AF=2CD
24.延长BD至点F,使DF=BC,连接EF.∵ AE=BD,△ABC为等边三角形,∴ BE=BF,∠B=60°,∴ △BEF为等边三角形,∴ ∠F=60°.在△ECB和△EDF中,BE=EF,∠B=∠F=60°,BC=DF.∴ △ECB≌△EDF,∴ EC=ED
25.画图如下.OD,ON,DM之间的数量关系为:OD=ON+DM或ON=OD+DM.分三种情况,①如图1,线段OD,ON,DM之间的数量关系为:OD=ON+DM,理由如下:∵ OC是角平分线,∴ ∠AOC=∠BOC.∵ CD∥OB,∴ ∠CME=∠ONE,∠C=∠BOC=∠AOC,∴ OD=CD.在△CEM和△OEN中,∠C=∠BOC,∠CME=∠ONE,CE=OE,∴ △CEM≌△OEN,∴ ON=CM,∴OD=CD=CM+DM=ON+DM.②如图2,由①易得OD=ON+DM.③如图3,类似①可证得OD=CD,△CEM≌△OEN,得ON=CM=CD+DM=OD+DM
26.(1) △CEF是等边三角形.理由:∵ △ACM与△BCN是等边三角形,∴ CA=CM,CN=CB,∠ACM=∠BCN=60°,∴ ∠ACN=∠BCM=120°,∴ △CAN≌△CMB,∴ AN=BM,∠CAN=∠CMB.∵ E,F分别为BM,AN的中点,∴ AF=ME,∴ △ACF≌△MCE,∴ CE=CF,∠ACF=∠MCE.∵ ∠ACF=∠ACM+∠MCF,∴ ∠MCE=∠MCF+∠FCE,即∠ECF=∠ACM=60°,∴ △CEF是等边三角形 (2) 不成立,理由如下:方法同(1)可得△CAN≌△CMB,△ACF≌△MCE,∴CE=CF,∠ACF=∠MCE.∵ ∠ACF=∠ACM+∠MCF,∴ ∠MCE=∠MCF+∠FCE,即∠ECF=∠ACM≠60°,∴ △CEF是等腰三角形
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
