圆的认识.

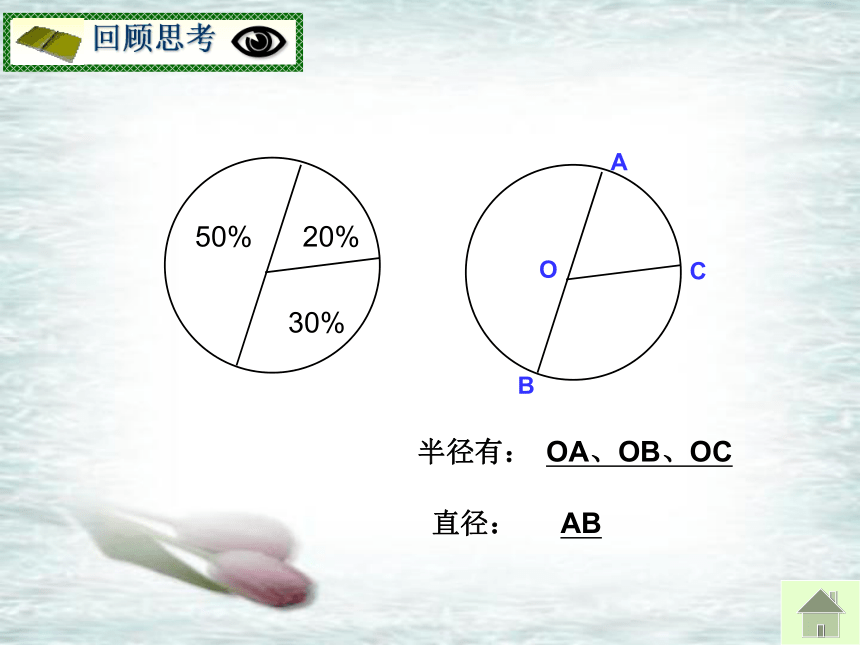
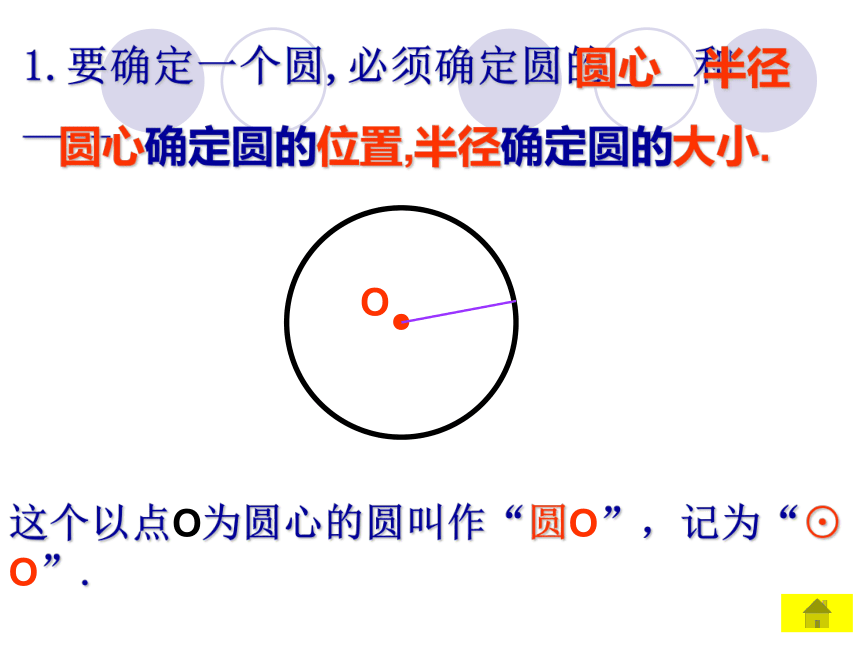
课件16张PPT。 圆的认识 圆一石激起千层浪乐在其中一、 创设情境 引入新课圆的世界奥运五环福建土楼一、 创设情境 引入新课圆的世界祥 子小憩片刻一、 创设情境 引入新课圆的世界50%20%30%OACB半径有：OA、OB、OC直径：AB●1.要确定一个圆,必须确定圆的____和____圆心半径圆心确定圆的位置,半径确定圆的大小.O这个以点O为圆心的圆叫作“圆O”，记为“⊙ O”.●OBCA 1.如图,半径有:______________OA、OB、OC若∠AOB=60°，
则△AOB是_____三角形. 2.如图,弦有:______________AB、BCAC在圆中有长度不等的弦，等边直径是圆中最长的弦。
●OBCA 1.如图,弧有:______________2 .劣弧有：优弧有：你知道优弧与劣弧的区别么？判断：半圆是弧，但弧不一定是半圆.( )CBOAFEDM 问：
（1）FC是弦吗？为什么？
（2）∠CMB， ∠CMA是不是圆心角？弦有：AB ， CD圆心角有： ∠DOE ， ∠COE1、圆是对称图形吗？它有哪些对称性？回顾： 圆既是轴对称图形，又是中心对称图
形,也是旋转对称图形。旋转角度可以是任
意度数。对称轴是过圆心任意一条直线。2、圆的对称轴在哪里，对称中心和旋转中心在哪里？ 将图中的扇形AOB绕点O逆时针旋转某个角度。在得到的图形中，同学们可以通过比较前后两个图形，发现有何关系？探究一：那么相等（或等圆）相等相等相等3.在同一个圆 中，如果弦相等，那么所对的圆心角_____、所对的弧______,所对的弦的弦心距_____。2.在同一个圆 中，如果弧相等，那么所对的圆心角_____、所对的弦______， 所对的弦的弦心距_____。1.在同一个圆 中，如果圆心角相等，那么它所对的弧相等、所对的弦相等, 所对的弦的弦心距也相等。 结论：相等以上三句话如没有在同圆或等圆中，这个结论还会成立吗？（或等圆）（或等圆）相等一.判断下列说法是否正确：
1相等的圆心角所对的弧相等。（ ）
2相等的弧所对的弦相等。（ ）
3相等的弦所对的弧相等。（ ）二.如图，⊙O中，AB=CD，
，则试一试你的能力×√×
如图，在⊙O中，AC=BD，
,求∠2的度数。
你会做吗？解：∵（已知）∴∴∴∠1=∠2=45°（在同圆中，相等的弧所对的圆心角相等）思考:在⊙O中,AB、CD是直径.AD与BC平行吗?说说你的理由.四边形ACBD是矩形么?为什么?温馨提示：对角线相等且互相平分的四边形是矩形。