二次函数y=ax2的图象和性质

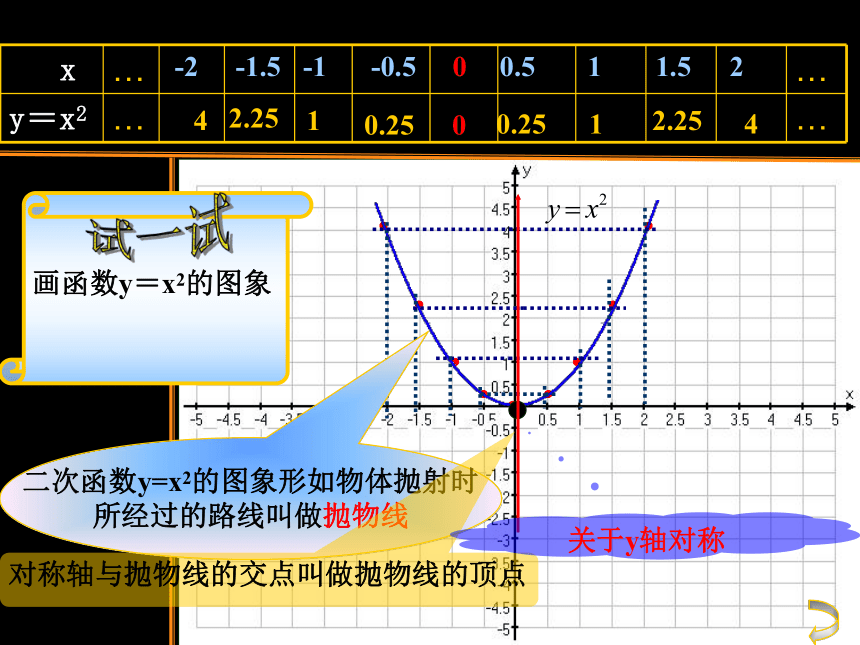
课件10张PPT。初三数学二次函数y=ax2的图象和性质石狮锦峰实验学校 蔡玉彬知识回顾一次函数 的图象是 ；反比例函数 的图象是 ； 问题1：二次函数y=x2的图象是什么呢？一条直线两支双曲线 函数图象画法列表描点连线 描点法问题2：如何画二次函数y=x2的图象呢？00.2512.2540.2512.254-0.50.511.52-1-1.5-2 0二次函数y=x2的图象形如物体抛射时
所经过的路线叫做抛物线对称轴与抛物线的交点叫做抛物线的顶点关于y轴对称画函数y＝x2的图象 函数图象向上向下y轴（直线x＝0）y轴（直线x＝0）（0，0）（0，0）当x＝0时，y最小值为0当x＝0时，y最大值为0动画演示二次函数y=ax2的性质议一议1、根据左边已画好的函数图象填空：
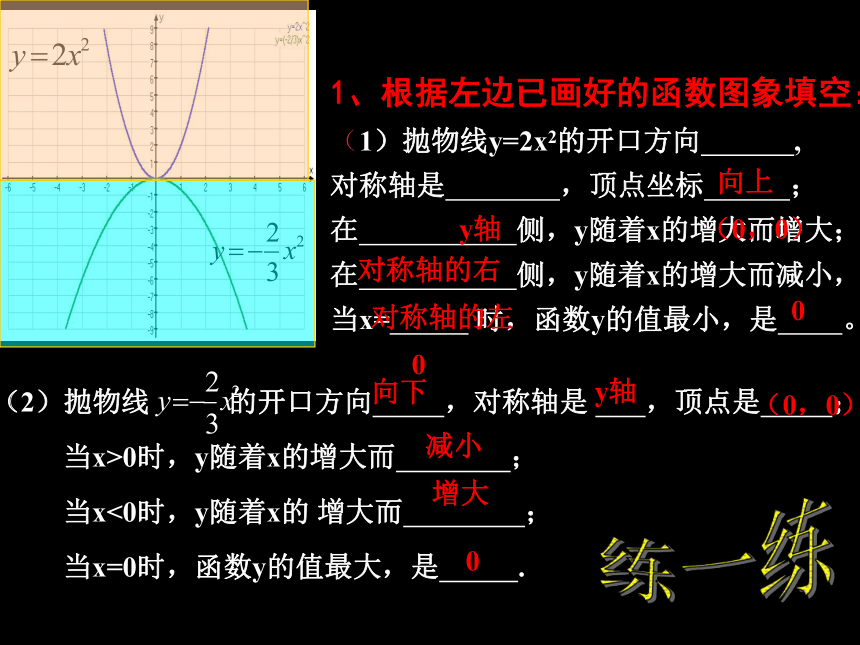
（1）抛物线y=2x2的开口方向 ,
对称轴是 ，顶点坐标 ；
在 侧，y随着x的增大而增大；
在 侧，y随着x的增大而减小，
当x= 时，函数y的值最小，是 。（2）抛物线 的开口方向 ，对称轴是 ，顶点是 ；
当x>0时，y随着x的增大而 ；
当x<0时，y随着x的 增大而 ；
当x=0时，函数y的值最大，是 .向上y轴（0，0）对称轴的右对称轴的左00向下y轴增大减小0（0，0）练一练2、已知二次函数y=ax2（a≠0）的图像经过点（-2，-8）。
（1）求a 的值，并写出这个二次函数的解析式；
（2）判断点（-1，-4）是否在此抛物线上；
（3）点 和 在此抛物线上，试比较a和b的大小。解（1）把（-2，-8）代入y=ax2,得
-8=a(-2)2,解出a= -2,
所求函数解析式为y= -2x2. （3）因为点 和 在抛物线y= -2x2上 所以当 时，
当 时，
因此 m 不在此抛物线上。(-2,-8)y=-2x2 因为 < 1 所以 m>n在对称轴的右边y随x的增大而减小通过本节的学习你有哪些收获呢？家庭作业:教材P6练习1、2、3、4 驶向胜利的彼岸课堂小结再见勇攀高峰 画一画：函数y＝x2和y＝-x2、y＝2x2和y＝-2x2、
y＝3x2和y＝-3x2，
（1）你发现它们之间有什么关系呢？（2）你能从函数y＝ax2和y＝－ax2得出什么结论呢？
画一画：(1)函数 ，当a取1、2、3、4 …… 时,
函数的开口大小有什么变化呢？
(2)函数 ，当a取-1、-2、-3、-4 ……时,
函数的开口大小有什么变化呢？