探索勾股定理

课件39张PPT。九年制义务教育北师大版实验教材八年级上册探索勾股定理深圳市景秀中学 李松涛说课环节教材分析教法学法教学评价大环节5教学过程教学理念一、教学设计理念 新课程倡导和突出“自主、合作、探究”的学习方式，使学生在玩中学、做中学、思考中学、合作中学。从而使“知识与技能、过程与方法、情感态度与价值观”的课程目标三位一体地得以实现。二、教材分析教材的地位与作用

几何学中的重要定理之一，揭示了直角
三角形中三边的数量关系。为解直角三角形
创造了边的等量关系；为“无理数”概念的引
入做了很好的知识铺垫。其发现、验证和应
用蕴涵着丰富的数学思想和科学研究方法。

学情分析1、 在学习本节内容之前，学生已经掌握了三角形三边的大小关系及等腰三角形、等边三角形的相关性质，对于直角三角形内角之间的数量关系也十分熟悉。
2、初步具备了在拼图中对图形进行割补、计算的能力.
1、知识目标： 了解勾股定理的面积证法、拼图证法及其
数形结合的思想，理解和掌握勾股定理的内
容及简单应用。
2、能力目标： 发展学生的合情推理意识，主动探究的习
惯，感受数形结合及从特殊到一般的思想
方法。3、情感目标: 培养学生不断发现、勇于探索新知的精神。
激发学生的探究欲望，使他们爱学、会学、
乐学。渗透爱国主义思想，激发学生学习
的兴趣。 教学目标 教学重点、难点与教学突破
（1）重点：勾股定理及其简单应用
（2）难点：勾股定理的证明---面积证法、 拼图证法
（3）教学突破：充分运用多种教学手段，创设问题情
境，发挥学生的主体作用，在实验中

探索，在探索中领悟、在领悟中理解。
三、教法学法及教学手段1. 教学方法: 创设情境、建构模型、引导探索、应用拓展 2. 学习方法: 自主探索、动手实践、合作交流、归纳总结
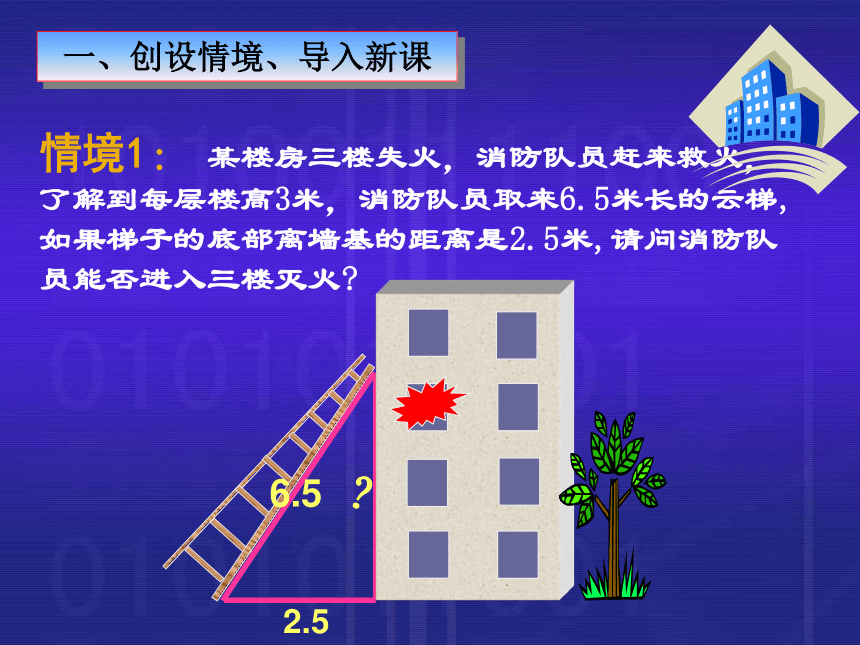
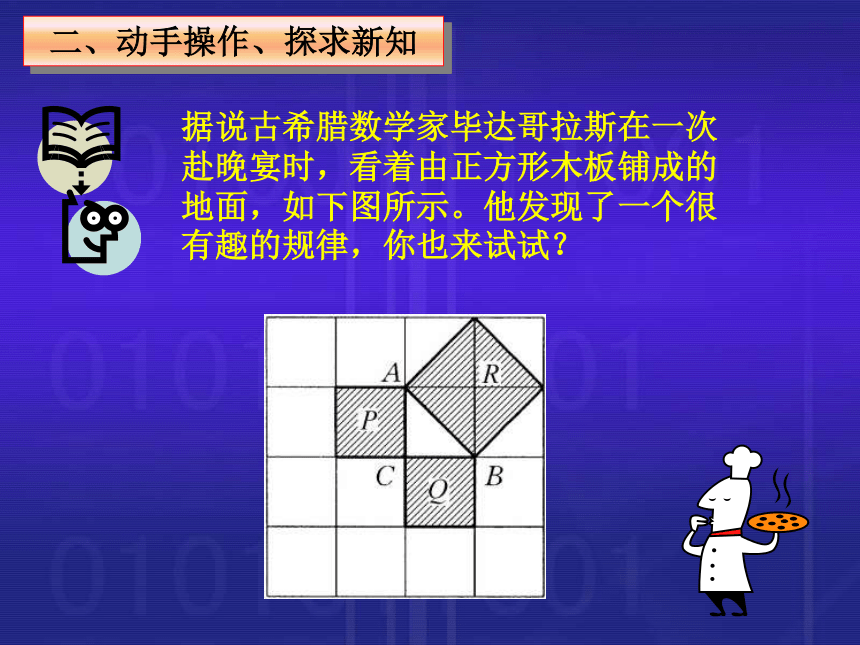
3. 教学手段: 借助电脑多媒体及几何画板进行辅助教学创设情境、导入新课动手操作、探求新知历史回顾、拓展视野归纳总结、应用知识总结反思、布置作业四、教学过程一、创设情境、导入新课情境1： 某楼房三楼失火，消防队员赶来救火，了解到每层楼高3米，消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火? 据说古希腊数学家毕达哥拉斯在一次赴晚宴时，看着由正方形木板铺成的地面，如下图所示。他发现了一个很有趣的规律，你也来试试？二、动手操作、探求新知？
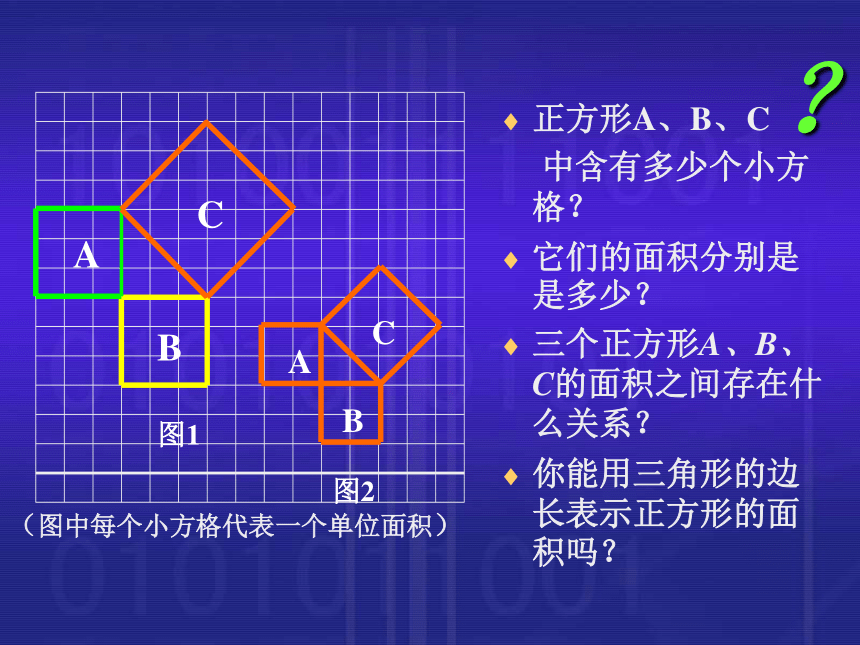
正方形A、B、C
中含有多少个小方格？
它们的面积分别是是多少？
三个正方形A、B、C的面积之间存在什么关系？
你能用三角形的边长表示正方形的面积吗？
结论： 面积A +面积B =面积C对于一般的直角三角形，正方形A、B、C的面积也有这样的关系吗？（图中每个小方格代表一个单位面积） 结论： 面积A +面积B =面积C1．正方形的边长即是直角三角形的边长。
2．正方形的面积即是直角三角形的边长的平方。
面积A + 面积B = 面积C　我们的发现bacBCA 你能用两种方法表示大正方形的面积吗？baccbacabab即：a2+b2=c2面积（ a-b）2即：a2+b2=c2勾股定理（gou－gu theorem） 如果直角三角形两直角边分别为a，b，斜边为c，那么 即直角三角形两直角边的平方和等于斜边的平方.a2 = c2 － b2 ，结论变形：b2 = c2 － a2a2 + b2 = c2 三、归纳总结、知识应用 1． 求出下列图中字母所代表的正方形的面积基础题设计意图：进一步巩固利用正方形面积验证定理的方法。2. 求下列用字母表示的边长设计意图：熟练掌握“在已知直角三角形三边中任意两
边的条件下，利用勾股定理求第三边”的方法。3.某楼房三楼失火，消防队员赶来救火，了解到每层楼高3米，消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火? 设计意图：定理应用，前后呼应。 4. 小明妈妈买了一部29英寸（74厘米）的电视机，小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你同意他的想法吗？你能解释这是为什么吗？想一想：58厘米46厘米74厘米设计意图：学数学、用数学。源于实践、用于实践。 勾股定理是数学中最重要的基本定理之
一, 20世纪80年代, 科学界曾征集有史以来科
学上的十大发现,结果数学界只有唯一的一条
入选, 它就是勾股定理. 勾股定理不但是最重
要的定理,而且也是证明方法最多的数学定理.四、历史回顾、拓展视野在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.《周髀算经》 毕达哥拉斯在国外，相传这个定理是公元前500多年，当时古希腊数学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。法国和比利时称它为“驴桥定理”，埃及称它为“埃及三角形”等。但他们发现的时间都比我国要迟得多。 1955年希腊曾发行了一枚纪念邮票 与外星人沟通的“勾股定理”图标2002年北京国际数学家大会会标美丽的勾股树 想一想?五、总结反思、布置作业数学日记：
1、本节课你学习了什么定理？
2、该定理揭示了哪一类三角形中的
什么元素之间的关系？
3、在验证定理的过程中，我们运用
了哪些证明方法？
4、你最有兴趣的是什么？你有没有
感到困难的地方？ 作业布置 1. 基础练习：P6 　2，3，4
　2. 探究练习：通过查询网络、书籍，收集有关勾
股定理的相关证明方法及其历史故事， 并与
你的同伴交流。
3. 利用周末去深圳科学馆参观“勾股弦定理”模型。
4. 拓展练习1. “印度荷花问题”湖静浪平六月天
荷花半尺出水面
忽来一阵狂风急
湖面之上不复见
入秋渔翁始发现
残花离根二尺遥
试问水深有几许？——印度数学家拜斯迦罗（公元1114——1185年）1、教学流程体现了知识发生、形成和发展的过程，
符合学生的认知结构和认知规律。
2、教学面向全体学生，坚持教学的民主性。尊重学
生的主体作用，尊重学生的创造性。
3、教法改革和学法指导同步进行；注重数学思想方
法的教学；体现了“方法比知识重要”这一新的教
学价值观。课堂学习成长记录卡五、教学评价设计意图:因为有课件辅助,所以板书以简洁,有条理,突出重点为主探索勾股定理如果直角三角形两直角边分别为a，b，斜边为c，那么a2 + b2 = c2解题过程无限风光在险峰！
探索的过程是艰辛的，
但探索的结果却是
令人回味无穷的！谢谢