2023-2024学年人教版九年级数学全册期末复习:第24章 圆 44张PPT
文档属性
| 名称 | 2023-2024学年人教版九年级数学全册期末复习:第24章 圆 44张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-21 21:59:15 | ||
图片预览



文档简介
(共45张PPT)
2023-2024学年九年级数学全册期末复习★★——圆
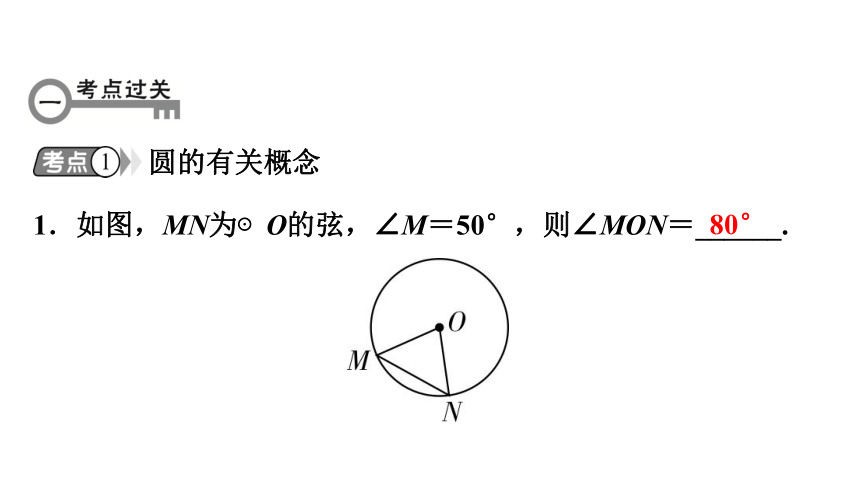
1.如图,MN为⊙O的弦,∠M=50°,则∠MON=______.
80°
圆的有关概念
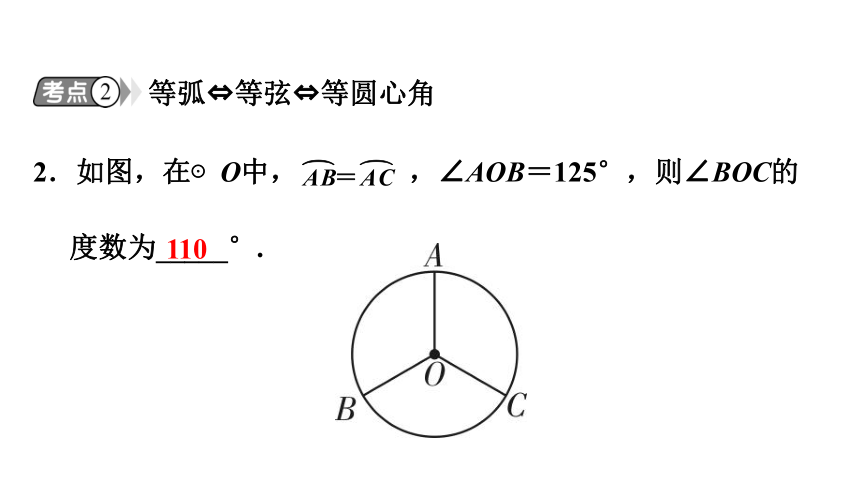
2.如图,在⊙O中, ,∠AOB=125°,则∠BOC的度数为_____°.
110
等弧 等弦 等圆心角
B
垂径定理
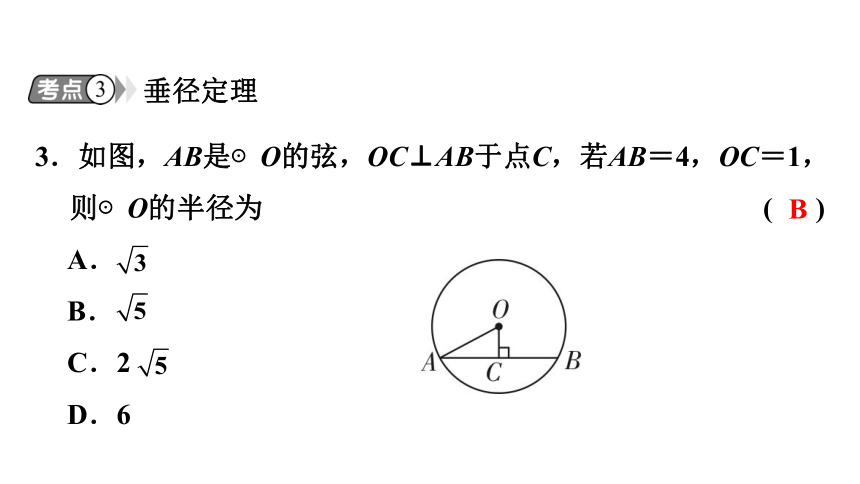
3.如图,AB是⊙O的弦,OC⊥AB于点C,若AB=4,OC=1,则⊙O的半径为 ( )
A.
B.
C.2
D.6
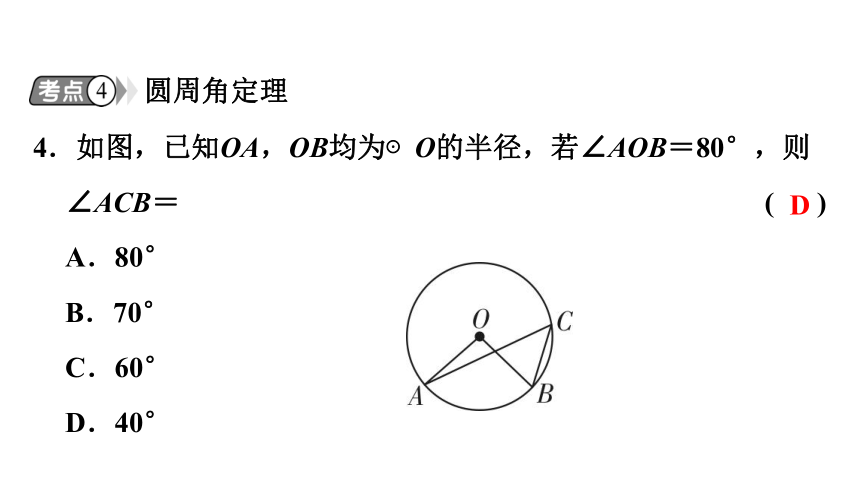
4.如图,已知OA,OB均为⊙O的半径,若∠AOB=80°,则∠ACB= ( )
A.80°
B.70°
C.60°
D.40°
D
圆周角定理
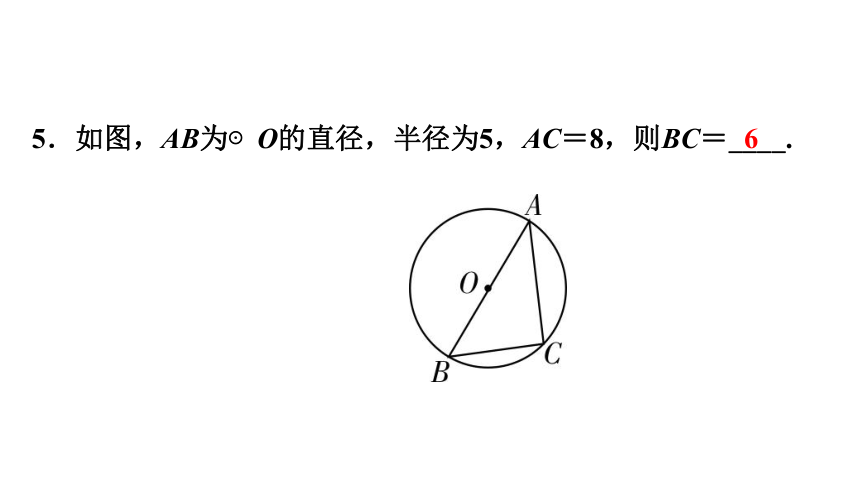
5.如图,AB为⊙O的直径,半径为5,AC=8,则BC=____.
6
6.如图,PA是⊙O的切线,A是切点,PA=4,OP=5,则⊙O的周长为_____(结果保留π).
6π
切线的性质、判定及切线长定理
7.如图,点P在⊙O外,PA,PB分别与⊙O相切于A,B两点,∠P=50°,则∠AOB= ( )
A.150°
B.130°
C.155°
D.135°
B
8.⊙O的半径为5 cm,点A到圆心O的距离OA=3 cm,则点A与⊙O的位置关系为 ( )
A.点A在圆上
B.点A在圆内
C.点A在圆外
D.无法确定
B
点与圆、直线与圆的位置关系
9.如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3 cm为半径作⊙A,当AB=____ cm时,BC与⊙A相切.
6
10.如图,点O为△ABC的内心,∠CAB=60°,∠ABC=40°,则∠AOB=_____°.
130
内心、外心、圆的内接四边形
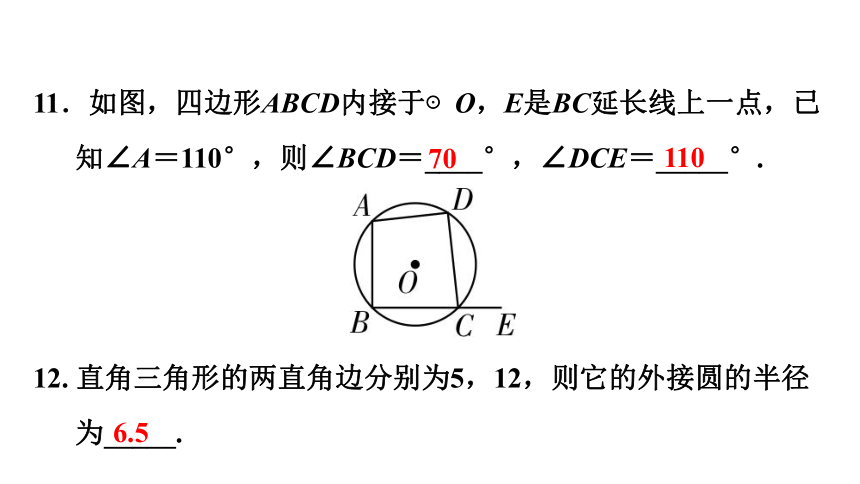
11.如图,四边形ABCD内接于⊙O,E是BC延长线上一点,已知∠A=110°,则∠BCD=____°,∠DCE=_____°.
12. 直角三角形的两直角边分别为5,12,则它的外接圆的半径为_____.
70
110
6.5
13.如图,⊙O是正三角形ABC的外接圆,OB=2,则△ABC的半径为___,中心角度数为______,边心距长为___,边长等于______ .
2
正多边形和圆
120°
1
14.如果一个正多边形的中心角为72°,那么这个正多边形的边数是 ( )
A.4
B.5
C.6
D.7
B
15.圆心角为120°的扇形的半径为3,则这个扇形的面积为____,所对的弧长为____.
16.如图,扇形的半径为3, 的长为4,则扇形面积为____.
3π
弧长、扇形面积
2π
6
17.如图,在Rt△AOC中,AO=3 cm, CO=4 cm,将△AOC绕CO旋转一周得到一个圆锥,则圆锥的侧面积为_________,全面积为_________.
15π cm2
圆锥的侧面积与全面积
24π cm2
18.如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4 ,以点A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分的面积是_______.
8-2π
求阴影面积
19.如图,在⊙O中,半径OA垂直弦BC,垂足为E.
(1)若∠EBO=30°,求∠ADC的度数;
解:(1)∵半径OA垂直弦BC,
又∵∠EBO=30°,
∴∠AOB=180°-∠OEB-∠EBO=180°-90°-30°
=60°.
∴ ,∠OEB=90°.
∴∠ADC= ∠AOB.
∴∠ADC= ×60°=30°.
(2)若BC=6,AE=1,求⊙O的半径.
解:(2)设⊙O半径为r,
在Rt△BOE中,OE=AO-AE=r-1,
由勾股定理,得r2=(r-1)2+32,
解得r=5.
BE= BC= ×6=3,OB=r,
20.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
解:(1)相切.证明如下:如图,连接OD,
∵∠CAD=∠DAO=∠ADO,
∴OD∥AC,
∴∠ODB=∠C=90°.
∴BC是⊙O的切线.
(2)若BD=2 ,BF=2,求阴影部分的面积.
解:(2)设OD=OF=x,
∵OD2+BD2=OB2,
解得x=2,
即在Rt△ODB中,OD=2,OB=4,∠ODB=90°.
∴∠B=30°.
∴∠DOB=60°.
∴S扇形DOF= π×22= π,S△BOD= ×2×2 =2 .
∴S阴影=S△BOD-S扇形DOF=2 - π.
∴x2+(2 )2=(x+2)2
21. 如图,AM为⊙O的切线,A为切点,过⊙O上一点B作BD⊥AM于点D,BD交⊙O于点C,OC平分∠AOB.
(1)求∠AOB的度数;
解:(1)∵AM为⊙O的切线,
∴OA⊥AM.
∵BD⊥AM,
∴∠OAD=∠BDM=90°.
∴OA∥BD.
∴∠AOC=∠OCB.
∵OB=OC,
∴∠OBC=∠OCB.
∵OC平分∠AOB,∴∠AOC=∠BOC.
∴∠BOC=∠OCB=∠OBC=60°.
∴∠AOB=120°.
解:(2)如图,过点O作OE⊥BD于点E,
(2)若⊙O的半径为2 cm,求CD的长.
∵∠BOC=∠OCB=∠OBC=60°,
∴△OBC是等边三角形.
∴BE=EC=1.
∵∠OED=∠EDA=∠OAD=90°,
∴四边形OADE是矩形.
∴DE=OA=2.
∴CD=DE-EC=2-1=1.
22.已知圆的半径是2 ,则该圆的内接正六边形的面积是
( )
A.3
B.9
C.18
D.36
C
23.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2 cm,扇形的圆心角θ=120°,则该圆锥的高h=______cm.
24.如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,点D是 上一点,且AC=CD,连接AD与BC交于点E,过点C作CF∥AD与BA的延长线交于点F.
(1)求证:CF是⊙O的切线;
(1)证明:如图,连接OC,交AD于点H,
∵AC=CD,
∴OC⊥AD,AH=DH.
∵CF∥AD,
∴∠FCO=∠AHO=90°,
∵OC是⊙O的半径,且CF⊥OC,
∴CF是⊙O的切线.
∴ ,
(2)若∠F=30°,AD=6,求CF的长.
(2)解:∠FCO=90°,∠F=30°,
∴∠AOC=60°,
∵∠BAD=∠F=30°,
∴∠D=∠BAD,
∴CD∥AF,
∴四边形ADCF是平行四边形,
∴CF=AD=6.
∴∠D= ∠AOC=30°,
25. 如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,CD=CE.
(1)求证:OA=OB;
(1)证明:如图,连接OC,
∵AB与⊙O相切于点C,
∴∠ACO=90°.
∵CD=CE,
∴∠AOC=∠BOC.
∴∠A=∠B.
∴OA=OB.
∴ .
(2)已知AB=4 ,OA=4,求阴影部分的面积.
(2)解:由(1)可知,△OAB是等腰三角形,
∴BC= AB=2 .
∴sin∠COB= = .∴∠COB=60°.
∴∠B=30°,∴OC= OB=2.
∴S扇形OCE= .
S△OCB= ×2 ×2=2 .
∴S阴影=2 - π.
26.如图,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(1)证明:连接OE,OC,
∵OB=OE,OC=OC,BC=EC,
∴△OCB≌△OCE(SSS).
∵DE是⊙O的切线,
∴∠OEC=90°.
∴∠B=∠OEC=90°.
∴BC为⊙O的切线.
(2)解:如图,过点D作DF⊥BC于点F,得矩形ABFD,
(2)若AB=2 ,AD=2,求线段BC的长.
设 BC=x,则CF=x-2,DC=x+2,
BF=AD=2,DF=AB=2 ,
在Rt△DFC中,根据勾股定理,得(x+2)2-(x-2)2=(2 )2,
解得x= ,
∴BC= .
27. 【教材变式】(P101第3题改编)如图,OC平分∠AOB,D是OC上任意一点,⊙D和OA相切于点E,连接CE.
(1)求证:OB与⊙D相切;
∵⊙D与OA相切于点E,
∴DE⊥OA.
∵OC平分∠AOB,
∴DF=DE.
∴OB与⊙D相切.
(1)证明:如图,连接DE,过点D作DF⊥OB于点F.
(2)解:如图,过点E作EG⊥OD于点G.
(2)若OE=4,⊙D的半径为3,求CE的长.
由(1)得DE⊥OA,∴∠OED=90°.
∵OE=4,DE=3,∴OD= =5.
∵EG⊥OD,∴ OD·EG= OE·DE.
∴EG= ∴DG=
∴CG=CD+DG=3+ = .
∴CE= .
28.如图,在⊙O中,AB是直径,D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为
的中点,连接DE,EB.
(1)求证:四边形BCDE是平行四边形;
(1)证明:∵CD是⊙O的切线,∠BOD=60°,
∴OD⊥CD,∠C=30°.
如图,连接OE,则∠AOE=60°.
∴∠EBA=∠C=∠DEB.
∴EB∥CD,ED∥BC.
∴四边形BCDE是平行四边形.
∴∠DEB= ∠BOD=30°.
∴∠EBA= ∠AOE=30°.
(2)已知图中阴影部分面积为6π,求⊙O的半径r.
(2)解:由(1)知OD⊥CD,
如图,设OD与EB的交点为H,
∴BH=HE.
∴△OBH≌△DEH.
∴阴影部分的面积与扇形OBD的面积相等.
解得r=6.
∴S阴影= =6π.
2023-2024学年九年级数学全册期末复习★★——圆
1.如图,MN为⊙O的弦,∠M=50°,则∠MON=______.
80°
圆的有关概念
2.如图,在⊙O中, ,∠AOB=125°,则∠BOC的度数为_____°.
110
等弧 等弦 等圆心角
B
垂径定理
3.如图,AB是⊙O的弦,OC⊥AB于点C,若AB=4,OC=1,则⊙O的半径为 ( )
A.
B.
C.2
D.6
4.如图,已知OA,OB均为⊙O的半径,若∠AOB=80°,则∠ACB= ( )
A.80°
B.70°
C.60°
D.40°
D
圆周角定理
5.如图,AB为⊙O的直径,半径为5,AC=8,则BC=____.
6
6.如图,PA是⊙O的切线,A是切点,PA=4,OP=5,则⊙O的周长为_____(结果保留π).
6π
切线的性质、判定及切线长定理
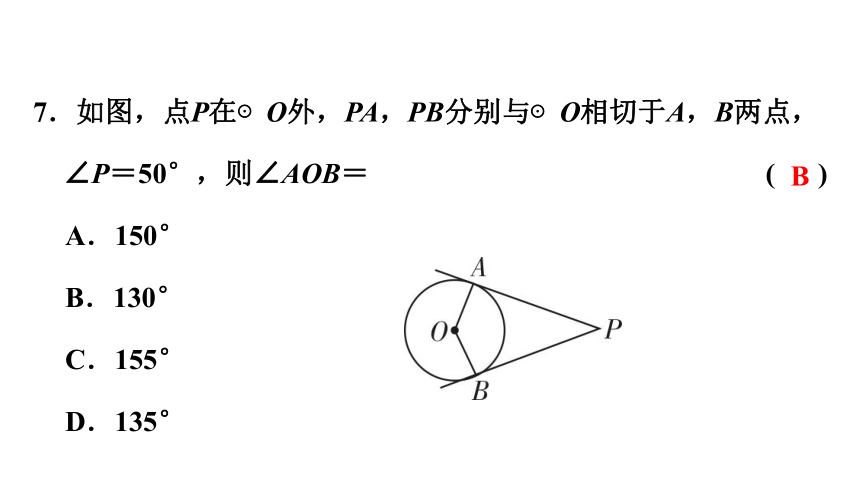
7.如图,点P在⊙O外,PA,PB分别与⊙O相切于A,B两点,∠P=50°,则∠AOB= ( )
A.150°
B.130°
C.155°
D.135°
B
8.⊙O的半径为5 cm,点A到圆心O的距离OA=3 cm,则点A与⊙O的位置关系为 ( )
A.点A在圆上
B.点A在圆内
C.点A在圆外
D.无法确定
B
点与圆、直线与圆的位置关系
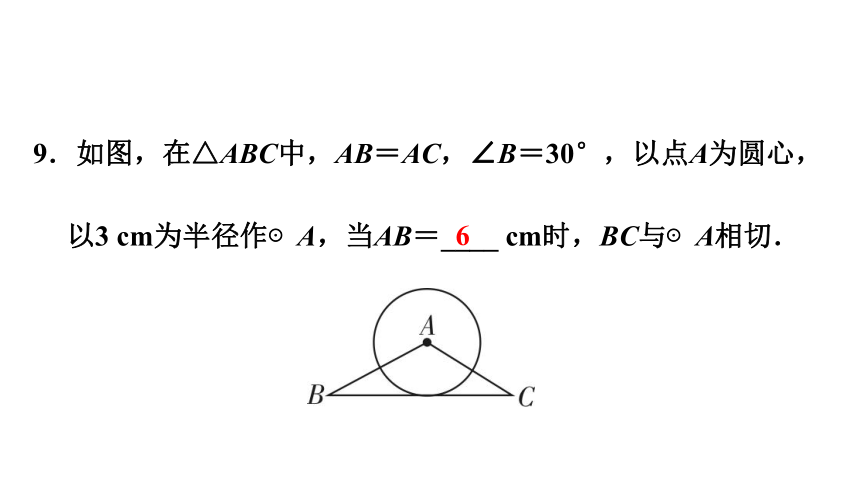
9.如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3 cm为半径作⊙A,当AB=____ cm时,BC与⊙A相切.
6
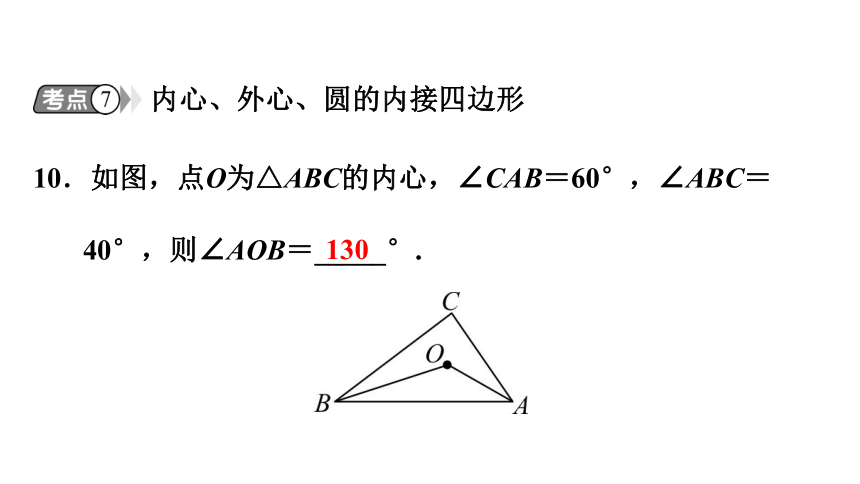
10.如图,点O为△ABC的内心,∠CAB=60°,∠ABC=40°,则∠AOB=_____°.
130
内心、外心、圆的内接四边形
11.如图,四边形ABCD内接于⊙O,E是BC延长线上一点,已知∠A=110°,则∠BCD=____°,∠DCE=_____°.
12. 直角三角形的两直角边分别为5,12,则它的外接圆的半径为_____.
70
110
6.5
13.如图,⊙O是正三角形ABC的外接圆,OB=2,则△ABC的半径为___,中心角度数为______,边心距长为___,边长等于______ .
2
正多边形和圆
120°
1
14.如果一个正多边形的中心角为72°,那么这个正多边形的边数是 ( )
A.4
B.5
C.6
D.7
B
15.圆心角为120°的扇形的半径为3,则这个扇形的面积为____,所对的弧长为____.
16.如图,扇形的半径为3, 的长为4,则扇形面积为____.
3π
弧长、扇形面积
2π
6
17.如图,在Rt△AOC中,AO=3 cm, CO=4 cm,将△AOC绕CO旋转一周得到一个圆锥,则圆锥的侧面积为_________,全面积为_________.
15π cm2
圆锥的侧面积与全面积
24π cm2
18.如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4 ,以点A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分的面积是_______.
8-2π
求阴影面积
19.如图,在⊙O中,半径OA垂直弦BC,垂足为E.
(1)若∠EBO=30°,求∠ADC的度数;
解:(1)∵半径OA垂直弦BC,
又∵∠EBO=30°,
∴∠AOB=180°-∠OEB-∠EBO=180°-90°-30°
=60°.
∴ ,∠OEB=90°.
∴∠ADC= ∠AOB.
∴∠ADC= ×60°=30°.
(2)若BC=6,AE=1,求⊙O的半径.
解:(2)设⊙O半径为r,
在Rt△BOE中,OE=AO-AE=r-1,
由勾股定理,得r2=(r-1)2+32,
解得r=5.
BE= BC= ×6=3,OB=r,
20.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
解:(1)相切.证明如下:如图,连接OD,
∵∠CAD=∠DAO=∠ADO,
∴OD∥AC,
∴∠ODB=∠C=90°.
∴BC是⊙O的切线.
(2)若BD=2 ,BF=2,求阴影部分的面积.
解:(2)设OD=OF=x,
∵OD2+BD2=OB2,
解得x=2,
即在Rt△ODB中,OD=2,OB=4,∠ODB=90°.
∴∠B=30°.
∴∠DOB=60°.
∴S扇形DOF= π×22= π,S△BOD= ×2×2 =2 .
∴S阴影=S△BOD-S扇形DOF=2 - π.
∴x2+(2 )2=(x+2)2
21. 如图,AM为⊙O的切线,A为切点,过⊙O上一点B作BD⊥AM于点D,BD交⊙O于点C,OC平分∠AOB.
(1)求∠AOB的度数;
解:(1)∵AM为⊙O的切线,
∴OA⊥AM.
∵BD⊥AM,
∴∠OAD=∠BDM=90°.
∴OA∥BD.
∴∠AOC=∠OCB.
∵OB=OC,
∴∠OBC=∠OCB.
∵OC平分∠AOB,∴∠AOC=∠BOC.
∴∠BOC=∠OCB=∠OBC=60°.
∴∠AOB=120°.
解:(2)如图,过点O作OE⊥BD于点E,
(2)若⊙O的半径为2 cm,求CD的长.
∵∠BOC=∠OCB=∠OBC=60°,
∴△OBC是等边三角形.
∴BE=EC=1.
∵∠OED=∠EDA=∠OAD=90°,
∴四边形OADE是矩形.
∴DE=OA=2.
∴CD=DE-EC=2-1=1.
22.已知圆的半径是2 ,则该圆的内接正六边形的面积是
( )
A.3
B.9
C.18
D.36
C
23.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2 cm,扇形的圆心角θ=120°,则该圆锥的高h=______cm.
24.如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,点D是 上一点,且AC=CD,连接AD与BC交于点E,过点C作CF∥AD与BA的延长线交于点F.
(1)求证:CF是⊙O的切线;
(1)证明:如图,连接OC,交AD于点H,
∵AC=CD,
∴OC⊥AD,AH=DH.
∵CF∥AD,
∴∠FCO=∠AHO=90°,
∵OC是⊙O的半径,且CF⊥OC,
∴CF是⊙O的切线.
∴ ,
(2)若∠F=30°,AD=6,求CF的长.
(2)解:∠FCO=90°,∠F=30°,
∴∠AOC=60°,
∵∠BAD=∠F=30°,
∴∠D=∠BAD,
∴CD∥AF,
∴四边形ADCF是平行四边形,
∴CF=AD=6.
∴∠D= ∠AOC=30°,
25. 如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,CD=CE.
(1)求证:OA=OB;
(1)证明:如图,连接OC,
∵AB与⊙O相切于点C,
∴∠ACO=90°.
∵CD=CE,
∴∠AOC=∠BOC.
∴∠A=∠B.
∴OA=OB.
∴ .
(2)已知AB=4 ,OA=4,求阴影部分的面积.
(2)解:由(1)可知,△OAB是等腰三角形,
∴BC= AB=2 .
∴sin∠COB= = .∴∠COB=60°.
∴∠B=30°,∴OC= OB=2.
∴S扇形OCE= .
S△OCB= ×2 ×2=2 .
∴S阴影=2 - π.
26.如图,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(1)证明:连接OE,OC,
∵OB=OE,OC=OC,BC=EC,
∴△OCB≌△OCE(SSS).
∵DE是⊙O的切线,
∴∠OEC=90°.
∴∠B=∠OEC=90°.
∴BC为⊙O的切线.
(2)解:如图,过点D作DF⊥BC于点F,得矩形ABFD,
(2)若AB=2 ,AD=2,求线段BC的长.
设 BC=x,则CF=x-2,DC=x+2,
BF=AD=2,DF=AB=2 ,
在Rt△DFC中,根据勾股定理,得(x+2)2-(x-2)2=(2 )2,
解得x= ,
∴BC= .
27. 【教材变式】(P101第3题改编)如图,OC平分∠AOB,D是OC上任意一点,⊙D和OA相切于点E,连接CE.
(1)求证:OB与⊙D相切;
∵⊙D与OA相切于点E,
∴DE⊥OA.
∵OC平分∠AOB,
∴DF=DE.
∴OB与⊙D相切.
(1)证明:如图,连接DE,过点D作DF⊥OB于点F.
(2)解:如图,过点E作EG⊥OD于点G.
(2)若OE=4,⊙D的半径为3,求CE的长.
由(1)得DE⊥OA,∴∠OED=90°.
∵OE=4,DE=3,∴OD= =5.
∵EG⊥OD,∴ OD·EG= OE·DE.
∴EG= ∴DG=
∴CG=CD+DG=3+ = .
∴CE= .
28.如图,在⊙O中,AB是直径,D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为
的中点,连接DE,EB.
(1)求证:四边形BCDE是平行四边形;
(1)证明:∵CD是⊙O的切线,∠BOD=60°,
∴OD⊥CD,∠C=30°.
如图,连接OE,则∠AOE=60°.
∴∠EBA=∠C=∠DEB.
∴EB∥CD,ED∥BC.
∴四边形BCDE是平行四边形.
∴∠DEB= ∠BOD=30°.
∴∠EBA= ∠AOE=30°.
(2)已知图中阴影部分面积为6π,求⊙O的半径r.
(2)解:由(1)知OD⊥CD,
如图,设OD与EB的交点为H,
∴BH=HE.
∴△OBH≌△DEH.
∴阴影部分的面积与扇形OBD的面积相等.
解得r=6.
∴S阴影= =6π.
同课章节目录
