数学人教A版(2019)必修第一册2.1等式与不等式性质(共30张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册2.1等式与不等式性质(共30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-21 08:58:48 | ||
图片预览











文档简介
(共30张PPT)
2.1 等式与不等式性质
第二章 一元二次函数、方程与不等式
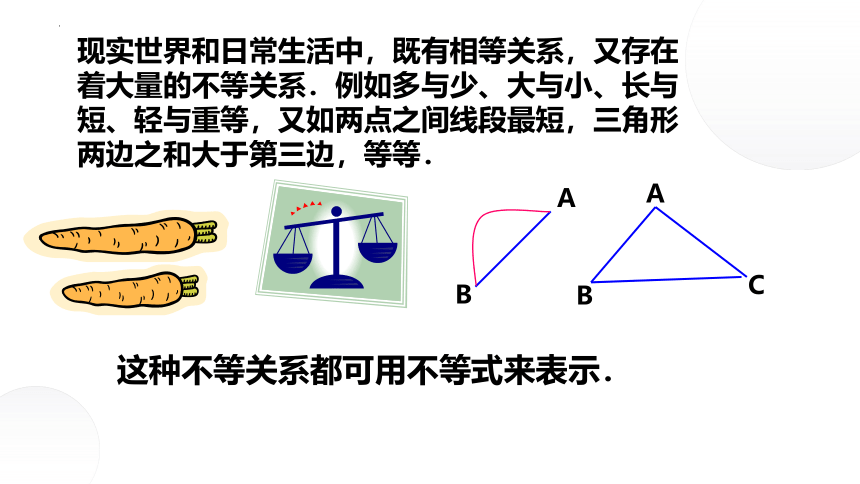
现实世界和日常生活中,既有相等关系,又存在着大量的不等关系.例如多与少、大与小、长与短、轻与重等,又如两点之间线段最短,三角形两边之和大于第三边,等等.
B
A
C
B
A
这种不等关系都可用不等式来表示.
1.限速40km/h的路标,指示司机在前方路段行驶时,
应使汽车的速度v不超过40km/h,写成不等式就是:
_____________.
2.某品牌酸奶的质检查规定,酸奶中脂肪的含量f
应不少于2.5%,蛋白质的含量p应不少于2.3%,写
成不等式组就是:
0f ≥ 2.5%,
p ≥ 2.3%
1.不等关系
一:不等关系与不等问题
讲授新知
常见的文字语言与符号语言之间的转换
文字语言 大于,高于,超过 小于,低于,少于 大于等于,至少,不低于 小于等于,至多,不超过
符号语言 __ __ ___ ___
>
<
≥
≤
问题1 设点A与平面 的距离为d,B为平面 上的任意一点,则d |AB|.
A
B
B
B
d
2.不等问题
≤
问题2 :某种杂志原以每本2.5元的价格销售,可以销售出8万本。据市场调查,若单价每提高0.1元,销售量就可能相应减少2000本,若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元呢?
元万本
单价提高元销量减少2000本
单价提高元销量减少2万本
解:设提价后每本杂志的单价为元,则销售总收入为万元.
于是,不等关系“销售总收入不低于20万元”可以用不等式表示为: ①
刮一刮
刮一刮
刮一刮
例1
刮一刮
刮一刮
刮一刮
例2
刮一刮
刮一刮
刮一刮
小奶茶
刮一刮
刮一刮
刮一刮
可乐
刮一刮
刮一刮
刮一刮
马卡龙
刮一刮
刮一刮
刮一刮
对点2
刮一刮
刮一刮
刮一刮
对点3
刮一刮
刮一刮
刮一刮
对点1
幸运抽抽抽
例1.某汽车公司因发展需要,需购进一批汽车,计划使用不超过1 000万元的资金购买单价分别为40万元、90万元的A型汽车和B型汽车,根据需要,A型汽车至少买5辆,B型汽车至少买6辆,写出满足上述所有不等关系的不等式(组).
解:设购买A型汽车和B型汽车分别为x辆、y辆,
探究 在初中,我们知道由于数轴上的点与实数一一对应,所以可以利用数轴上点的位置关系来规定实数的大小关系,具体是如何规定的呢?
设a,b是两个实数,它们在数轴上所对应的点分别是A,B.那么,当点A在点B的左边时,ab.
关于两个实数大小关系的基本事实:
1、一个事实:
(1)对于任意两个实数a、b,在a>b,a= b,a<b三种关系中有且仅有一种成立.
(2)判断两个实数大小:
比较两个实数a与b的大小,归结为判断它们的差a-b的符号
二:不等式的性质
例1.比较和的大小.
解:∵
∴
这里,我们借助多项式减法运算,得出了一个明显大于0的数(式).这是解决不等式问题的常用方法.
0是正数与负数的分界点,它为实数比较大小提供了“标杆”.
例2.已知,比较与的大小.
变2.(1)已知,比较与的大小.
解(1):∵
变2.(2)比较与的大小.
刮一刮
刮一刮
刮一刮
例1
刮一刮
刮一刮
刮一刮
例2
刮一刮
刮一刮
刮一刮
小奶茶
刮一刮
刮一刮
刮一刮
可乐
刮一刮
刮一刮
刮一刮
马卡龙
刮一刮
刮一刮
刮一刮
对点2
刮一刮
刮一刮
刮一刮
对点3
刮一刮
刮一刮
刮一刮
对点1
幸运抽抽抽
对点2已知a>0,比较与的大小.
对点3.已知0解:
新知探索
右图是在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客.你能在这个图中找出一些相等关系和不等关系吗?
将图中的“风车”抽象成图.在正方形中有4个全等的直角三角形.
新知探索
设直角三角形的两条直角边的长为,那么正方形的边长为.
由于正方形的面积大于4个直角三角形的面积和,我们就得到了一个不等式:
这样,4个直角三角形的面积和为,正方形的面积为.
新知探索
当直角三角形变为等腰直角三角形,即时,正方形缩为一个点,这时有:
于是就有
新知探索
一般地,,有,
当且仅当时,等号成立.
事实上,利用完全平方公式,得:
因为,,
当且仅当时,等号成立,所以.
因此,由两个实数大小关系的基本事实,
得,当且仅当时,等号成立.
练习
实际应用
用一段长为30的篱笆围成一个一遍靠墙的矩形菜园,墙长18,要求菜园的面积不小于110靠墙的一边长为试用不等式表示其中的不等关系.
解:由于矩形菜园靠墙的一边长为,而墙长为18,∴
这时菜园的另一条边长为
因此菜园的面积
依题意有即
故该题中的不等式关系表示为
练习
变1.用一段长为30的篱笆围成一个一遍靠墙的矩形菜园,墙长18,要求矩形菜园的长宽都不能超过11,靠墙的一边长为试用不等式表示其中的不等关系.
解:由于矩形菜园靠墙的一边长为,
这时菜园的另一条边长为
而矩形的长宽都不能超过11,
∴有
即.
练习
方法技巧:
1.用不等式(组)表示不等关系的步骤:
(1)审清题意,明确条件中的不等关系的个数;
(2)适当设未知数表示变量;
(3)用不等式表示每一个不等关系,并写成不等式组的形式.
2.用不等式表示不等关系的注意点
(1)利用不等式表示不等关系时,应注意必须是具有相同性质,可以比较大小的两个量才可用,没有可比性的两个量之间不能用不等式来表示.
(2)在用不等式表示实际问题时,一定要注意单位统一.
练习
方法技巧:
比较两个实数(代数式)大小的步骤:
(1)作差.对要比较大小的两个实数(或式子)作差;
(2)变形.对差进行变形;
(3)判断差的符号.结合变形的结果及题设条件判断差的符号;
(4)得出结论.
上述步骤可概括为“三步一结论”,这里的“判断符号”是目的,“变形”是关键.在变形中,一般变得越彻底,越有利于下一步的判断.其中变形的技巧较多,常见的有因式分解法、配方法、有理化法等.
思考.
用今天所学的数学知识来解释生活中“糖水加糖甜更甜”的现象.
谢谢学习
2.1 等式与不等式性质
第二章 一元二次函数、方程与不等式
现实世界和日常生活中,既有相等关系,又存在着大量的不等关系.例如多与少、大与小、长与短、轻与重等,又如两点之间线段最短,三角形两边之和大于第三边,等等.
B
A
C
B
A
这种不等关系都可用不等式来表示.
1.限速40km/h的路标,指示司机在前方路段行驶时,
应使汽车的速度v不超过40km/h,写成不等式就是:
_____________.
2.某品牌酸奶的质检查规定,酸奶中脂肪的含量f
应不少于2.5%,蛋白质的含量p应不少于2.3%,写
成不等式组就是:
0
p ≥ 2.3%
1.不等关系
一:不等关系与不等问题
讲授新知
常见的文字语言与符号语言之间的转换
文字语言 大于,高于,超过 小于,低于,少于 大于等于,至少,不低于 小于等于,至多,不超过
符号语言 __ __ ___ ___
>
<
≥
≤
问题1 设点A与平面 的距离为d,B为平面 上的任意一点,则d |AB|.
A
B
B
B
d
2.不等问题
≤
问题2 :某种杂志原以每本2.5元的价格销售,可以销售出8万本。据市场调查,若单价每提高0.1元,销售量就可能相应减少2000本,若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元呢?
元万本
单价提高元销量减少2000本
单价提高元销量减少2万本
解:设提价后每本杂志的单价为元,则销售总收入为万元.
于是,不等关系“销售总收入不低于20万元”可以用不等式表示为: ①
刮一刮
刮一刮
刮一刮
例1
刮一刮
刮一刮
刮一刮
例2
刮一刮
刮一刮
刮一刮
小奶茶
刮一刮
刮一刮
刮一刮
可乐
刮一刮
刮一刮
刮一刮
马卡龙
刮一刮
刮一刮
刮一刮
对点2
刮一刮
刮一刮
刮一刮
对点3
刮一刮
刮一刮
刮一刮
对点1
幸运抽抽抽
例1.某汽车公司因发展需要,需购进一批汽车,计划使用不超过1 000万元的资金购买单价分别为40万元、90万元的A型汽车和B型汽车,根据需要,A型汽车至少买5辆,B型汽车至少买6辆,写出满足上述所有不等关系的不等式(组).
解:设购买A型汽车和B型汽车分别为x辆、y辆,
探究 在初中,我们知道由于数轴上的点与实数一一对应,所以可以利用数轴上点的位置关系来规定实数的大小关系,具体是如何规定的呢?
设a,b是两个实数,它们在数轴上所对应的点分别是A,B.那么,当点A在点B的左边时,a
关于两个实数大小关系的基本事实:
1、一个事实:
(1)对于任意两个实数a、b,在a>b,a= b,a<b三种关系中有且仅有一种成立.
(2)判断两个实数大小:
比较两个实数a与b的大小,归结为判断它们的差a-b的符号
二:不等式的性质
例1.比较和的大小.
解:∵
∴
这里,我们借助多项式减法运算,得出了一个明显大于0的数(式).这是解决不等式问题的常用方法.
0是正数与负数的分界点,它为实数比较大小提供了“标杆”.
例2.已知,比较与的大小.
变2.(1)已知,比较与的大小.
解(1):∵
变2.(2)比较与的大小.
刮一刮
刮一刮
刮一刮
例1
刮一刮
刮一刮
刮一刮
例2
刮一刮
刮一刮
刮一刮
小奶茶
刮一刮
刮一刮
刮一刮
可乐
刮一刮
刮一刮
刮一刮
马卡龙
刮一刮
刮一刮
刮一刮
对点2
刮一刮
刮一刮
刮一刮
对点3
刮一刮
刮一刮
刮一刮
对点1
幸运抽抽抽
对点2已知a>0,比较与的大小.
对点3.已知0
新知探索
右图是在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客.你能在这个图中找出一些相等关系和不等关系吗?
将图中的“风车”抽象成图.在正方形中有4个全等的直角三角形.
新知探索
设直角三角形的两条直角边的长为,那么正方形的边长为.
由于正方形的面积大于4个直角三角形的面积和,我们就得到了一个不等式:
这样,4个直角三角形的面积和为,正方形的面积为.
新知探索
当直角三角形变为等腰直角三角形,即时,正方形缩为一个点,这时有:
于是就有
新知探索
一般地,,有,
当且仅当时,等号成立.
事实上,利用完全平方公式,得:
因为,,
当且仅当时,等号成立,所以.
因此,由两个实数大小关系的基本事实,
得,当且仅当时,等号成立.
练习
实际应用
用一段长为30的篱笆围成一个一遍靠墙的矩形菜园,墙长18,要求菜园的面积不小于110靠墙的一边长为试用不等式表示其中的不等关系.
解:由于矩形菜园靠墙的一边长为,而墙长为18,∴
这时菜园的另一条边长为
因此菜园的面积
依题意有即
故该题中的不等式关系表示为
练习
变1.用一段长为30的篱笆围成一个一遍靠墙的矩形菜园,墙长18,要求矩形菜园的长宽都不能超过11,靠墙的一边长为试用不等式表示其中的不等关系.
解:由于矩形菜园靠墙的一边长为,
这时菜园的另一条边长为
而矩形的长宽都不能超过11,
∴有
即.
练习
方法技巧:
1.用不等式(组)表示不等关系的步骤:
(1)审清题意,明确条件中的不等关系的个数;
(2)适当设未知数表示变量;
(3)用不等式表示每一个不等关系,并写成不等式组的形式.
2.用不等式表示不等关系的注意点
(1)利用不等式表示不等关系时,应注意必须是具有相同性质,可以比较大小的两个量才可用,没有可比性的两个量之间不能用不等式来表示.
(2)在用不等式表示实际问题时,一定要注意单位统一.
练习
方法技巧:
比较两个实数(代数式)大小的步骤:
(1)作差.对要比较大小的两个实数(或式子)作差;
(2)变形.对差进行变形;
(3)判断差的符号.结合变形的结果及题设条件判断差的符号;
(4)得出结论.
上述步骤可概括为“三步一结论”,这里的“判断符号”是目的,“变形”是关键.在变形中,一般变得越彻底,越有利于下一步的判断.其中变形的技巧较多,常见的有因式分解法、配方法、有理化法等.
思考.
用今天所学的数学知识来解释生活中“糖水加糖甜更甜”的现象.
谢谢学习
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
