人教版八年级数学上册试题 第11章《三角形》单元测试(含答案)
文档属性
| 名称 | 人教版八年级数学上册试题 第11章《三角形》单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 306.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 10:53:35 | ||
图片预览


文档简介
第11章三角形单元测试
一、选择题(本大题共10小题,每小题3分,共30分).
1.正多边形的每个内角都是144°,则它的边数是( )
A.10 B.13 C.15 D.19
2.已知三角形的两边长分别为3cm和9cm,则此三角形的第三边长可能是( )
A.3cm B.6cm C.9cm D.13cm
3.下列图形具中有稳定性的是( )
A.正方形 B.正五边形 C.三角形 D.四边形
4.如图,图中x的值为( )
A.40 B.50 C.60 D.70
5.如图,在△ABC中,∠A=55°,∠C=65°,BD平分∠ABC,DE∥BC,则∠BDE的度数是( )
A.50° B.25° C.30° D.35°
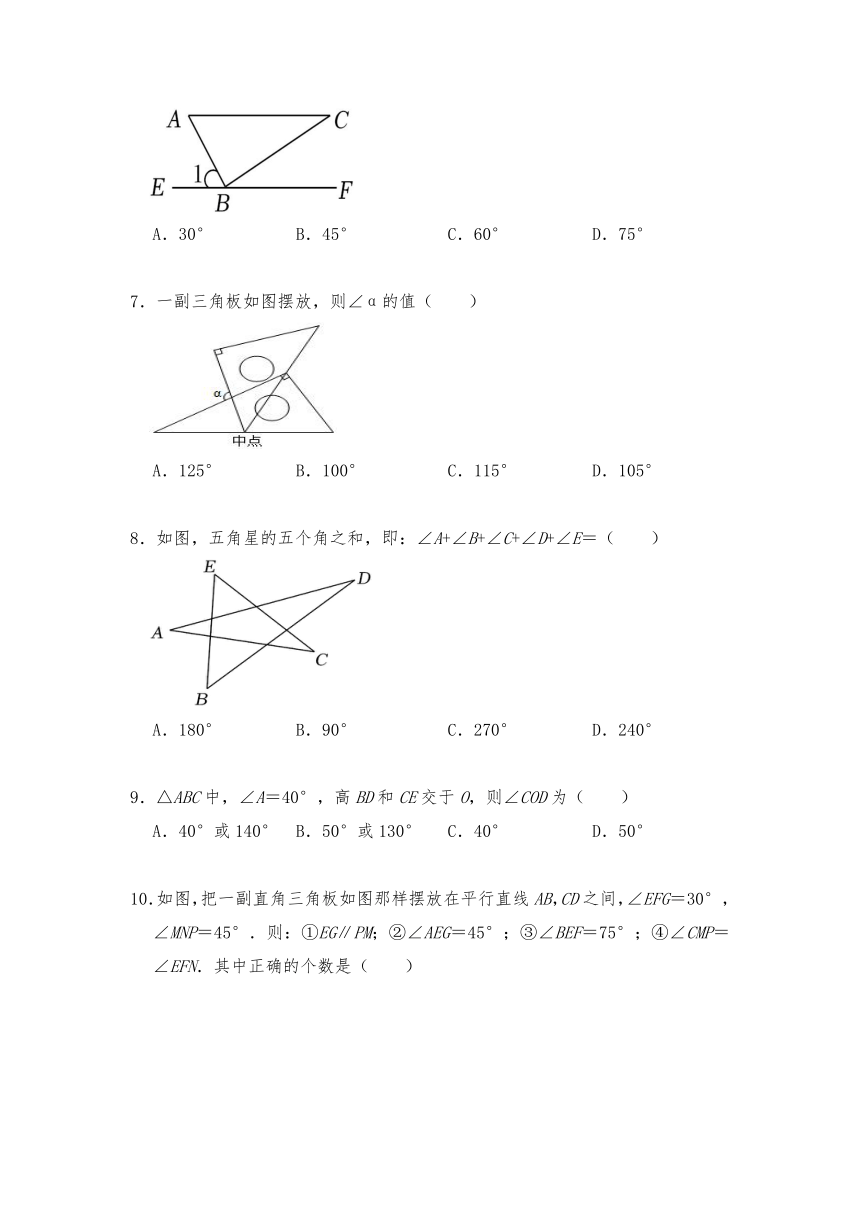
6.如图,把一块三角板ABC的直角顶点B放在直线EF上,∠C=30°,AC∥EF,则∠1=( )
A.30° B.45° C.60° D.75°
7.一副三角板如图摆放,则∠α的值( )
A.125° B.100° C.115° D.105°
8.如图,五角星的五个角之和,即:∠A+∠B+∠C+∠D+∠E=( )
A.180° B.90° C.270° D.240°
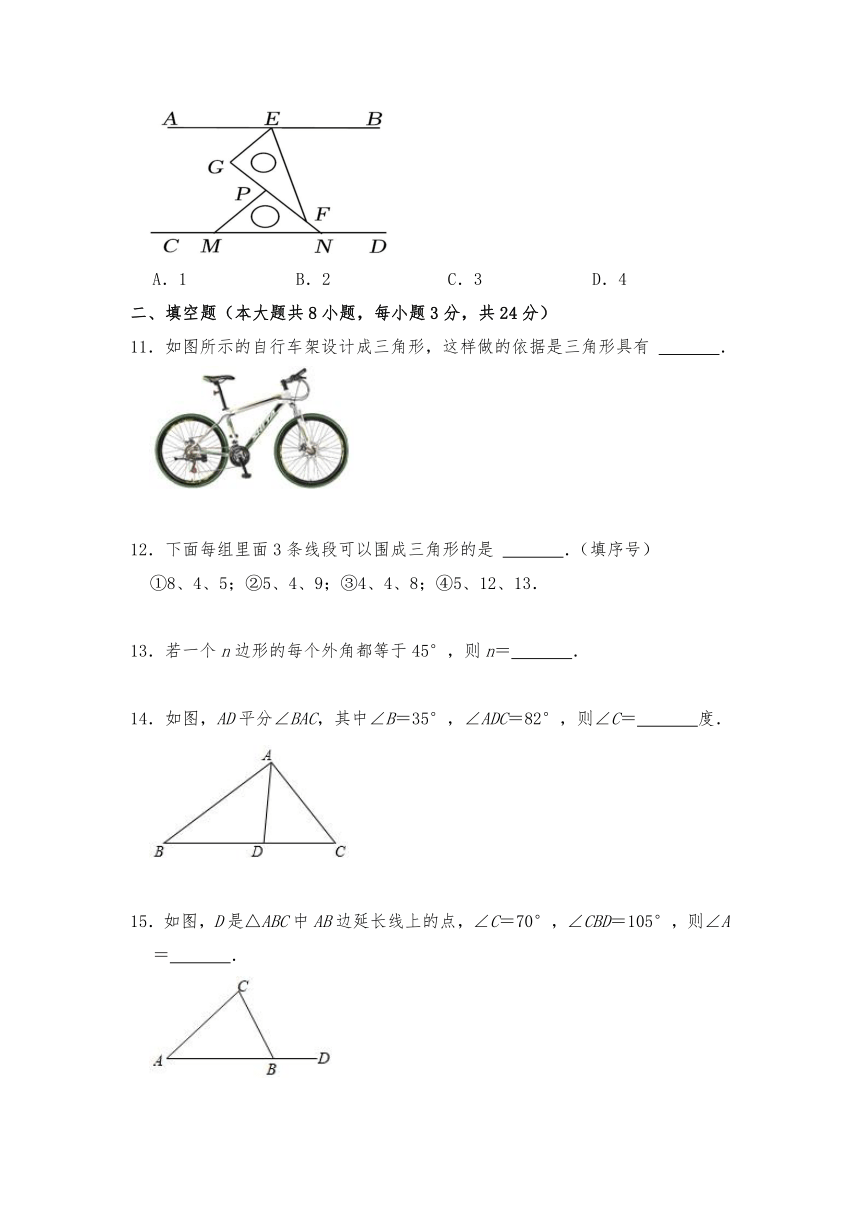
9.△ABC中,∠A=40°,高BD和CE交于O,则∠COD为( )
A.40°或140° B.50°或130° C.40° D.50°
10.如图,把一副直角三角板如图那样摆放在平行直线AB,CD之间,∠EFG=30°,∠MNP=45°.则:①EG∥PM;②∠AEG=45°;③∠BEF=75°;④∠CMP=∠EFN.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共8小题,每小题3分,共24分)
11.如图所示的自行车架设计成三角形,这样做的依据是三角形具有 .
12.下面每组里面3条线段可以围成三角形的是 .(填序号)
①8、4、5;②5、4、9;③4、4、8;④5、12、13.
13.若一个n边形的每个外角都等于45°,则n= .
14.如图,AD平分∠BAC,其中∠B=35°,∠ADC=82°,则∠C= 度.
15.如图,D是△ABC中AB边延长线上的点,∠C=70°,∠CBD=105°,则∠A= .
16.已知△ABC的三边长分别为a,b,c,则|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a+b|= .
17.如图所示,在△ABC中,∠B=60°,∠ACB=2∠A,将其折叠,使点B落在AC上的E点处,折痕为CD,则∠EDA= 度.
18.已知AD、AE分别是△ABC的角平分线和高线,∠B=50°.若∠DAE=10°,则∠BAC= °.
三、解答题(本大题共6小题,共46分.)
19.如图,在△ABC中,AD是高,AE是角平分线,∠B=36°,∠C=60°.
(1)求∠DAE的度数;
(2)若∠C﹣∠B=20°,直接写出∠DAE的度数.
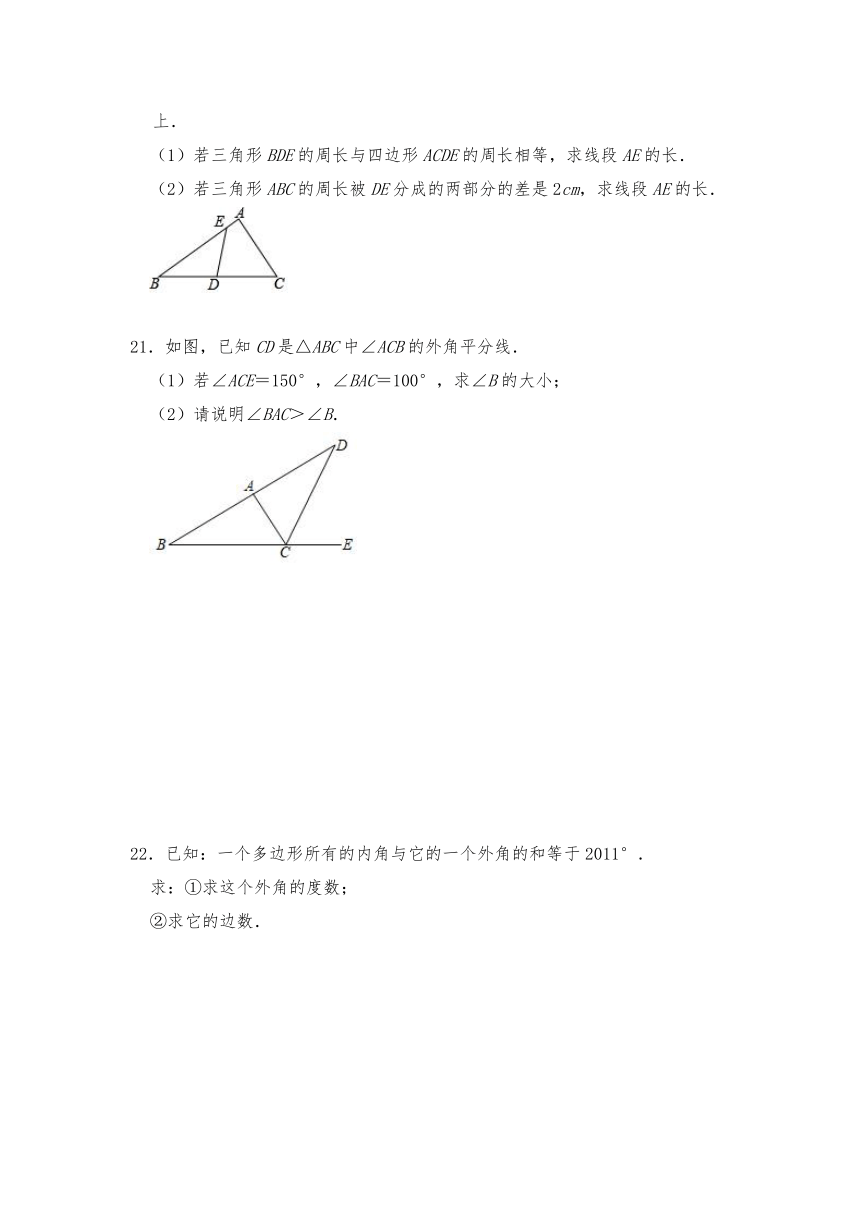
20.如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上.
(1)若三角形BDE的周长与四边形ACDE的周长相等,求线段AE的长.
(2)若三角形ABC的周长被DE分成的两部分的差是2cm,求线段AE的长.
21.如图,已知CD是△ABC中∠ACB的外角平分线.
(1)若∠ACE=150°,∠BAC=100°,求∠B的大小;
(2)请说明∠BAC>∠B.
22.已知:一个多边形所有的内角与它的一个外角的和等于2011°.
求:①求这个外角的度数;
②求它的边数.
23.阅读并解决下列问题:
(1)如图①,△ABC中,∠A=60°,∠ABC、∠ACB的平分线交于点D,则∠BDC= .
(2)如图②,五边形ABCDE中,AE∥BC,EF平分∠AED,CF平分∠BCD,若∠EDC=72°,求∠EFC的度数.
24.已知:△ABC中,记∠BAC=α,∠ACB=β.
(1)如图1,若AP平分∠BAC,BP、CP分别平分△ABC的外角∠CBM和∠BCN,BD⊥AP于点D.
①用α的代数式表示∠BPC的度数;
②用β的代数式表示∠PBD的度数;
(2)如图2,若点P为△ABC的三条内角平分线的交点,且BD⊥AP于点D.
①请补全图形;
②猜想(1)中的两个结论是否发生变化?如果不变,请说明理由;如果变化,直接写出正确的结论.
答案
一、选择题
A.C.C.C.C.C.D.A.C.C.
二.填空题
11.稳定性.
12.①④.
13.8.
14.51.
15.35°.
16.﹣a+b+3c.
17.20.
18.60或100.
三.解答题
19.解:(1)∵AD是高,
∴∠ADC=90°,
∵∠C=60°,
∴∠DAC=30°,
∵∠B=36°,∠C=60°,
∴∠BAC=180°﹣36°﹣60°=84°,
∵AE是角平分线,
∴∠CAE=42°,
∴∠DAE=42°﹣30°=12°;
(2)∠DAE=10°,理由如下:
∵AD是高,
∴∠ADC=90°,
∴∠DAC=90°﹣∠C,
∵∠BAC=180°﹣∠B﹣∠C,
又∵AE是角平分线,
∴∠CAE=∠BAC=(180°﹣∠B﹣∠C),
∴∠DAE=∠CAE﹣∠DAC=(∠C﹣∠B),
∵∠C﹣∠B=20°,
∴∠DAE=10°.
20.解:(1)由图可知三角形BDE的周长=BE+BD+DE,四边形ACDE的周长=AE+AC+DC+DE,
又三角形BDE的周长与四边形ACDE的周长相等,D为BC中点,
∴BD=DC,BE+BD+DE=AE+AC+DC+DE,
即BE=AE+AC,
∵AB=10cm,AC=6cm,
∴10﹣AE=AE+6,
∴AE=2cm.
(2)由三角形ABC的周长被DE分成的两部分的差是2,可得方程
①BE=AE+AC+2或②BE=AE+AC﹣2.
解①得AE=1cm,解②得AE=3cm.
故AE长为1cm或3cm.
21.解:(1)∵∠ACE=150°,∠BAC=100°,
∴∠B=∠ACE﹣∠BAC=150°﹣100°=50°;
(2)∵CD是△ABC中∠ACB的外角平分线,
∴∠ACD=∠ECD,
∵∠BAC是△ACD的外角,
∴∠BAC>∠ACD,
∴∠BAC>∠ECD,
∵∠ECD是△BCD的外角,
∴∠ECD>∠B,
∴∠BAC>∠B.
22.解:①∵一个多边形的所有内角与它的一个外角的和等于2011°,2011°÷180°=11…31°,
∴这个外角的度数是31°;
②∵一个多边形的所有内角与它的一个外角的和等于2011°,2011°÷180°=11…31°,
∴这个多边形的边数为:11+2=13.
23.解:(1)∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵∠ABC、∠ACB的平分线交于点D,
∴∠ABD=∠DBC,∠DCB=∠ACD,
∴∠DBC+∠DCB=120°÷2=60°,
∴∠BDC=180°﹣60°=120°,
故答案为:120°;
(2)∵AE∥BC,
∴∠A+∠B=180°,
∵五边形ABCDE的内角和是540°,
∴∠AED+∠EDC+∠BCD=540°﹣180°=360°,
∵∠EDC=72°,
∴∠AED+∠BCD=360°﹣72°=288°,
∵EF平分∠AED,CF平分∠BCD,
∴∠FED+∠FCD=288°÷2=144°,
∴∠EFC=360°﹣(∠FED+∠FCD+∠EDC)=360°﹣(144°+72°)=144°
24.解:(1)①如图1∵BP、CP分别平分△ABC的外角∠CBM和∠BCN
∴∠PBC=∠PBM=∠CBM=(α+β)
∠1=∠BCN=(180°﹣β)
∴∠BPC=180°﹣∠PBC﹣∠1
=180°﹣(α+β)﹣(180°﹣β)
=90°﹣α;
②在Rt△PBD中,∠PBD=90°﹣∠BPD,
∵∠BPD=∠PBM﹣∠2
=(α+β)﹣α
=β
∴∠PBD=90°﹣β;
(2)①如图2所示,
②中的两个结论发生了变化,
∵∠BAC=α,
∴∠ABC+∠ACB=180°﹣α,
∵点P为△ABC的三条内角平分线的交点,
∴∠PBC=ABC,∠PCB=ACB,
∴∠PBC+∠PCB=(∠ABC+∠ACB),
∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB)=90°+α;
∵∠BPD=∠BAP+∠ABP=(∠ABC+∠BAC)=(180°﹣∠ACB)=90°﹣β,
∵BD⊥AD,
∴∠ADB=90°,
∴∠PBD=90°﹣(90°﹣β)=.
一、选择题(本大题共10小题,每小题3分,共30分).
1.正多边形的每个内角都是144°,则它的边数是( )
A.10 B.13 C.15 D.19
2.已知三角形的两边长分别为3cm和9cm,则此三角形的第三边长可能是( )
A.3cm B.6cm C.9cm D.13cm
3.下列图形具中有稳定性的是( )
A.正方形 B.正五边形 C.三角形 D.四边形
4.如图,图中x的值为( )
A.40 B.50 C.60 D.70
5.如图,在△ABC中,∠A=55°,∠C=65°,BD平分∠ABC,DE∥BC,则∠BDE的度数是( )
A.50° B.25° C.30° D.35°
6.如图,把一块三角板ABC的直角顶点B放在直线EF上,∠C=30°,AC∥EF,则∠1=( )
A.30° B.45° C.60° D.75°
7.一副三角板如图摆放,则∠α的值( )
A.125° B.100° C.115° D.105°
8.如图,五角星的五个角之和,即:∠A+∠B+∠C+∠D+∠E=( )
A.180° B.90° C.270° D.240°
9.△ABC中,∠A=40°,高BD和CE交于O,则∠COD为( )
A.40°或140° B.50°或130° C.40° D.50°
10.如图,把一副直角三角板如图那样摆放在平行直线AB,CD之间,∠EFG=30°,∠MNP=45°.则:①EG∥PM;②∠AEG=45°;③∠BEF=75°;④∠CMP=∠EFN.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共8小题,每小题3分,共24分)
11.如图所示的自行车架设计成三角形,这样做的依据是三角形具有 .
12.下面每组里面3条线段可以围成三角形的是 .(填序号)
①8、4、5;②5、4、9;③4、4、8;④5、12、13.
13.若一个n边形的每个外角都等于45°,则n= .
14.如图,AD平分∠BAC,其中∠B=35°,∠ADC=82°,则∠C= 度.
15.如图,D是△ABC中AB边延长线上的点,∠C=70°,∠CBD=105°,则∠A= .
16.已知△ABC的三边长分别为a,b,c,则|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a+b|= .
17.如图所示,在△ABC中,∠B=60°,∠ACB=2∠A,将其折叠,使点B落在AC上的E点处,折痕为CD,则∠EDA= 度.
18.已知AD、AE分别是△ABC的角平分线和高线,∠B=50°.若∠DAE=10°,则∠BAC= °.
三、解答题(本大题共6小题,共46分.)
19.如图,在△ABC中,AD是高,AE是角平分线,∠B=36°,∠C=60°.
(1)求∠DAE的度数;
(2)若∠C﹣∠B=20°,直接写出∠DAE的度数.
20.如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上.
(1)若三角形BDE的周长与四边形ACDE的周长相等,求线段AE的长.
(2)若三角形ABC的周长被DE分成的两部分的差是2cm,求线段AE的长.
21.如图,已知CD是△ABC中∠ACB的外角平分线.
(1)若∠ACE=150°,∠BAC=100°,求∠B的大小;
(2)请说明∠BAC>∠B.
22.已知:一个多边形所有的内角与它的一个外角的和等于2011°.
求:①求这个外角的度数;
②求它的边数.
23.阅读并解决下列问题:
(1)如图①,△ABC中,∠A=60°,∠ABC、∠ACB的平分线交于点D,则∠BDC= .
(2)如图②,五边形ABCDE中,AE∥BC,EF平分∠AED,CF平分∠BCD,若∠EDC=72°,求∠EFC的度数.
24.已知:△ABC中,记∠BAC=α,∠ACB=β.
(1)如图1,若AP平分∠BAC,BP、CP分别平分△ABC的外角∠CBM和∠BCN,BD⊥AP于点D.
①用α的代数式表示∠BPC的度数;
②用β的代数式表示∠PBD的度数;
(2)如图2,若点P为△ABC的三条内角平分线的交点,且BD⊥AP于点D.
①请补全图形;
②猜想(1)中的两个结论是否发生变化?如果不变,请说明理由;如果变化,直接写出正确的结论.
答案
一、选择题
A.C.C.C.C.C.D.A.C.C.
二.填空题
11.稳定性.
12.①④.
13.8.
14.51.
15.35°.
16.﹣a+b+3c.
17.20.
18.60或100.
三.解答题
19.解:(1)∵AD是高,
∴∠ADC=90°,
∵∠C=60°,
∴∠DAC=30°,
∵∠B=36°,∠C=60°,
∴∠BAC=180°﹣36°﹣60°=84°,
∵AE是角平分线,
∴∠CAE=42°,
∴∠DAE=42°﹣30°=12°;
(2)∠DAE=10°,理由如下:
∵AD是高,
∴∠ADC=90°,
∴∠DAC=90°﹣∠C,
∵∠BAC=180°﹣∠B﹣∠C,
又∵AE是角平分线,
∴∠CAE=∠BAC=(180°﹣∠B﹣∠C),
∴∠DAE=∠CAE﹣∠DAC=(∠C﹣∠B),
∵∠C﹣∠B=20°,
∴∠DAE=10°.
20.解:(1)由图可知三角形BDE的周长=BE+BD+DE,四边形ACDE的周长=AE+AC+DC+DE,
又三角形BDE的周长与四边形ACDE的周长相等,D为BC中点,
∴BD=DC,BE+BD+DE=AE+AC+DC+DE,
即BE=AE+AC,
∵AB=10cm,AC=6cm,
∴10﹣AE=AE+6,
∴AE=2cm.
(2)由三角形ABC的周长被DE分成的两部分的差是2,可得方程
①BE=AE+AC+2或②BE=AE+AC﹣2.
解①得AE=1cm,解②得AE=3cm.
故AE长为1cm或3cm.
21.解:(1)∵∠ACE=150°,∠BAC=100°,
∴∠B=∠ACE﹣∠BAC=150°﹣100°=50°;
(2)∵CD是△ABC中∠ACB的外角平分线,
∴∠ACD=∠ECD,
∵∠BAC是△ACD的外角,
∴∠BAC>∠ACD,
∴∠BAC>∠ECD,
∵∠ECD是△BCD的外角,
∴∠ECD>∠B,
∴∠BAC>∠B.
22.解:①∵一个多边形的所有内角与它的一个外角的和等于2011°,2011°÷180°=11…31°,
∴这个外角的度数是31°;
②∵一个多边形的所有内角与它的一个外角的和等于2011°,2011°÷180°=11…31°,
∴这个多边形的边数为:11+2=13.
23.解:(1)∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵∠ABC、∠ACB的平分线交于点D,
∴∠ABD=∠DBC,∠DCB=∠ACD,
∴∠DBC+∠DCB=120°÷2=60°,
∴∠BDC=180°﹣60°=120°,
故答案为:120°;
(2)∵AE∥BC,
∴∠A+∠B=180°,
∵五边形ABCDE的内角和是540°,
∴∠AED+∠EDC+∠BCD=540°﹣180°=360°,
∵∠EDC=72°,
∴∠AED+∠BCD=360°﹣72°=288°,
∵EF平分∠AED,CF平分∠BCD,
∴∠FED+∠FCD=288°÷2=144°,
∴∠EFC=360°﹣(∠FED+∠FCD+∠EDC)=360°﹣(144°+72°)=144°
24.解:(1)①如图1∵BP、CP分别平分△ABC的外角∠CBM和∠BCN
∴∠PBC=∠PBM=∠CBM=(α+β)
∠1=∠BCN=(180°﹣β)
∴∠BPC=180°﹣∠PBC﹣∠1
=180°﹣(α+β)﹣(180°﹣β)
=90°﹣α;
②在Rt△PBD中,∠PBD=90°﹣∠BPD,
∵∠BPD=∠PBM﹣∠2
=(α+β)﹣α
=β
∴∠PBD=90°﹣β;
(2)①如图2所示,
②中的两个结论发生了变化,
∵∠BAC=α,
∴∠ABC+∠ACB=180°﹣α,
∵点P为△ABC的三条内角平分线的交点,
∴∠PBC=ABC,∠PCB=ACB,
∴∠PBC+∠PCB=(∠ABC+∠ACB),
∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB)=90°+α;
∵∠BPD=∠BAP+∠ABP=(∠ABC+∠BAC)=(180°﹣∠ACB)=90°﹣β,
∵BD⊥AD,
∴∠ADB=90°,
∴∠PBD=90°﹣(90°﹣β)=.
