人教版八年级数学上册试题 第十一章 三角形 单元测试(含答案)
文档属性
| 名称 | 人教版八年级数学上册试题 第十一章 三角形 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 235.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 10:49:49 | ||
图片预览




文档简介
第十一章 三角形单元测试
一、选择题(本大题共10小题,每小题3分,共30分).
1.下列事物所运用的原理不属于三角形稳定性的是( )
A.长方形门框的斜拉条 B.埃及金字塔
C.三角形房架 D.学校的电动伸缩大门
2.已知三角形两边长分别为2cm和5cm,则该三角形第三边的长可能是( )
A.3cm B.6cm C.7cm D.9cm
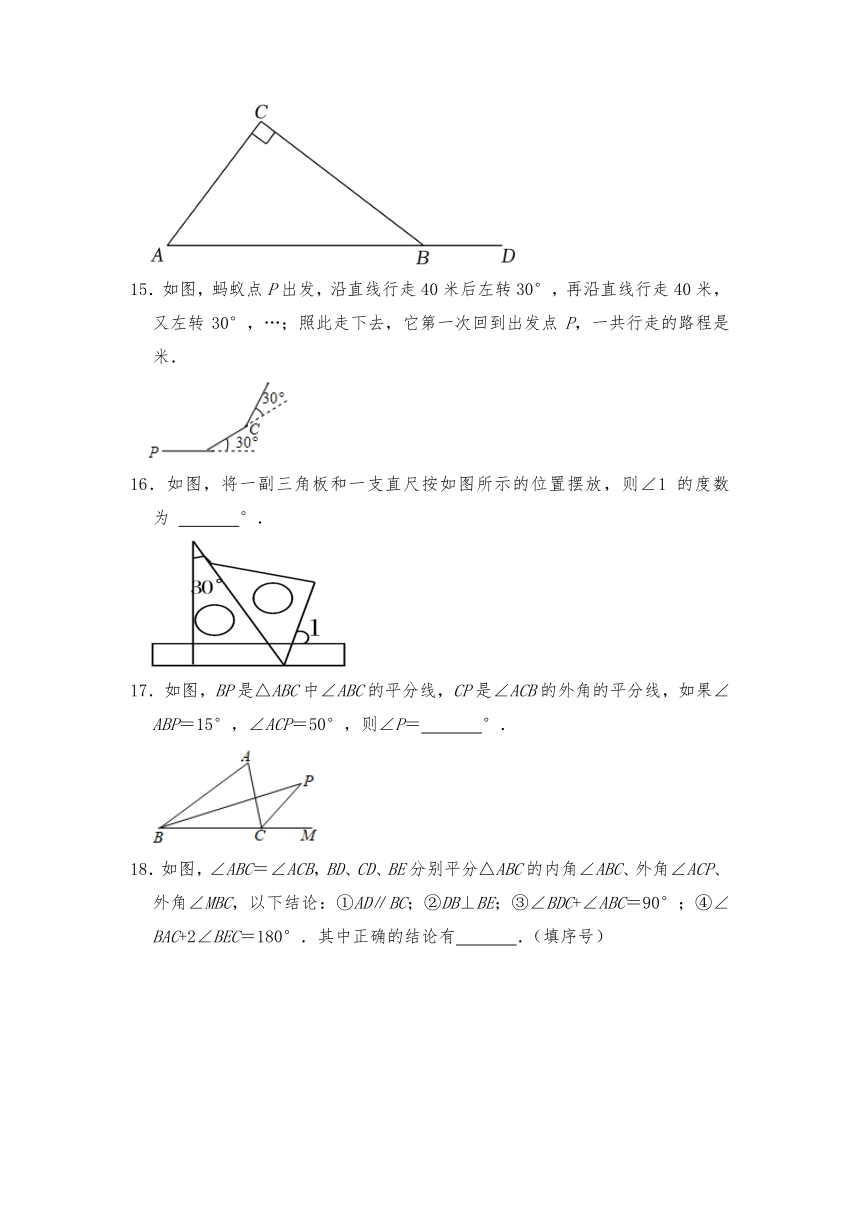
3.如图,在△ABC中,BC边的高是( )
A.CE B.CD C.AC D.AF
4.如图所示,直线m∥n,直角三角形ABC(∠C=90°)的顶点A在直线n上,若∠β=43°,则∠α的度数为( )
A.47° B.43° C.57° D.53°
5.如图,点E、F分别在AB、CD上,∠B=40°,∠C=60°,则∠1+∠2等于( )
A.70° B.80° C.90° D.100°
6.在下列条件中,不能判定△ABC是直角三角形的是( )
A.3∠A=2∠B=∠C B.∠A+∠B=∠C
C.∠A=50°,∠B=40° D.∠A=∠B=∠C
7.将一副普通的直角三角尺ADE和ABC如图放置,点D恰好落在BC边上,三角尺中∠ABC=60°,较长的边AE∥BC,则∠FAD的度数是( )
A.30° B.25° C.10° D.15°
8.定义:当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么这个“特征角”α的度数为( )
A.48° B.96°
C.88°或48° D.48°或96°或88°
9.如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC; ②∠ACB=2∠ADB; ③DB平分∠ADC; ④∠ADC=90°﹣∠ABD; ⑤∠BDC=∠BAC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.如图,直线a∥b,Rt△ABC的直角顶点A落在直线a上,点B落在直线b上,若∠1=15°,∠2=25°,则∠ABC的大小为( )
A.40° B.45° C.50° D.55°
二、填空题(本大题共8小题,每小题3分,共24分)
11.内角和是1440°的多边形的边数是 .
12.如图△ABC中,AB=21,AC=20,AD为中线,则△ABD与△ACD的周长之差= .
13.如图,在四边形ABCD中,∠1=∠2=∠A=30°,则∠ADB= .
14.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,点D是AB延长线上一点,则∠CBD的度数是 .
15.如图,蚂蚁点P出发,沿直线行走40米后左转30°,再沿直线行走40米,又左转30°,…;照此走下去,它第一次回到出发点P,一共行走的路程是 米.
16.如图,将一副三角板和一支直尺按如图所示的位置摆放,则∠1的度数为 °.
17.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=15°,∠ACP=50°,则∠P= °.
18.如图,∠ABC=∠ACB,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC,以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠BAC+2∠BEC=180°.其中正确的结论有 .(填序号)
三、解答题(本大题共6小题,共46分.)
19.如图所示,已知AD是△ABC的边BC上的中线.
(1)作出△ABD的边BD上的高.
(2)若△ABC的面积为10,求△ADC的面积.
(3)若△ABD的面积为6,且BD边上的高为3,求BC的长.
20.如图,已知AD是△ABC的中线,∠B=33°,∠BAD=21°,△ABD的周长比△ADC的周长大2,且AB=5.
(1)求∠ADC的度数;
(2)求AC的长.
21.如图,△ABC中,D为BC上一点,∠C=∠BAD,△ABC的角平分线BE交AD于点F.
(1)求证:∠AEF=∠AFE;
(2)G为BC上一点,当FE平分∠AFG且∠C=30°时,求∠CGF的度数.
22.如图,∠CAD与∠CBD的角平分线交于点P.
(1)若∠C=35°,∠D=29°,求∠P的度数;
(2)猜想∠D,∠C,∠P的等量关系.
23.(1)如图1,在△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D,若∠ABC=75°,∠ACB=45°,求∠D的度数.
(2)如图2,在四边形MNCB中,BD平分∠MBC,且与四边形MNCB的外角∠NCE的角平分线交于点D,若∠BMN=130°,∠CNM=100°,求∠D的度数.
24.[问题背景]
(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B=∠C+∠D.
[简单应用](可直接使用问题(1)中的结论)
(2)如图2,AP、CP分别平分∠BAD、∠BCD,
①若∠ABC=28°,∠ADC=20°,求∠P的度数;
②∠D和∠B为任意角时,其他条件不变,试直接写出∠P与∠D、∠B之间数量关系.
[问题探究]
(3)如图3,直线BP平分∠ABC的邻补角∠FBC,DP平分∠ADC的邻补角∠ADE,
①若∠A=30°,∠C=18°,则∠P的度数为 ;
②∠A和∠C为任意角时,其他条件不变,试直接写出∠P与∠A、∠C之间数量关系.
[拓展延伸]
(4)在图4中,若设∠C=x,∠B=y,∠CAP=∠CAB,∠CDP=∠CDB,试问∠P与∠C、∠B之间的数量关系为 ;(用x、y的代数式表示∠P)
(5)在图5中,直线BP平分∠ABC,DP平分∠ADC的外角∠ADE,猜想∠P与∠A、∠C的关系,直接写出结论 .
答案
一、选择题
D.B.D.A.D.A.D.D.D.C.
二.填空题
11.10.
12.1.
13.120°.
14.140°.
15.480.
16.75.
17.35.
18.①②③④.
三.解答题
19.解:(1)如图所示:
(2)∵AD是△ABC的边BC上的中线,△ABC的面积为10,
∴△ADC的面积=△ABC的面积=5.
(3)∵AD是△ABC的边BC上的中线,△ABD的面积为6,
∴△ABC的面积为12,
∵BD边上的高为3,
∴BC=12×2÷3=8.
20.解:(1)∵∠B=33°,∠BAD=21°,∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=33°+21°=54°;
(2)∵AD是BC边上中线,
∴BD=CD,
∴△ABD的周长﹣△ADC的周长=AB﹣AC,
∵△ABD的周长比△ADC的周长大2,且AB=5.
∴5﹣AC=2,即AC=3.
21.解:(1)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABF+∠BAD=∠CBE+∠C,
∵∠AFE=∠ABF+∠BAD,∠AEF=∠CBE+∠C,
∴∠AEF=∠AFE;
(2)∵FE平分∠AFG,
∴∠AFE=∠GFE,
∵∠AEF=∠AFE,
∴∠AEF=∠GFE,
∴FG∥AC,
∵∠C=30°,
∴∠CGF=180°﹣∠C=150°.
22.解:(1)设∠CAD=2x,∠CBD=2y,
根据∠CAD和∠CBD的角平分线相交于点P可知:
∠CAP=∠PAD=x,∠CBP=∠DBP=y,
∵三角形的内角和等于180°,∠C=35°,∠D=29°,
∴∠C+∠CAD=∠D+∠CBD,即35°+2x=29°+2y①.
∵∠AEB是△APE与△DBE的外角,
∴∠P+∠EAP=∠D+∠DBP,即∠P+x=29°+y②.
同理,∵∠AFB是△ACF与△BFP的外角,
∴∠C+∠CAP=∠P+∠CBP,即35°+x=∠P+y③,
①﹣②得,y=x+35°﹣∠P④,
①﹣③得,x=y+29°﹣∠P⑤,
④代入⑤得,x=x+35°﹣∠P+29°﹣∠P,
2∠P=35°+29°,
解得∠P=32°;
(2)∠P=(∠C+∠D),理由如下:
由(1)同理可知:
2∠P=∠C+∠D,
解得∠P=(∠C+∠D).
23.解:(1)∵BD平分∠ABC,CD平分∠ACE,
∴,.
∵∠ACE=∠ABC+∠A,∠DCE=∠DBC+∠D,
∴=,即,
∴.
∵∠ABC=75°,∠ACB=45°,∠A=60°,
∴∠D=30°.
(2)如图,延长BM,CN交于点A.
∵∠BMN=∠ANM+∠A,∠CNM=∠AMN+∠A,
∴∠A=∠BMN+∠CNM﹣180°=50°,
由(1)知.
24.解:(1)如图1中,
∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)①如图2中,
设∠BAP=∠PAD=x,∠BCP=∠PCD=y,
则有,
∴∠B﹣∠P=∠P﹣∠D,
∴∠P=(∠B+∠D)=(28°+20°)=24°;
②2∠P=∠B+∠D;
(3)①如图3中,设∠CBJ=∠JBF=x,∠ADP=∠PDE=y.
则有,
∴2∠P=∠A+∠C,
∴∠P=(30°+18°)=24°;
故答案为:24°;
②设∠CBJ=∠JBF=x,∠ADP=∠PDE=y.
则有,
∴2∠P=∠A+∠C;
(4)如图4中,设∠CAP=α,∠CDP=β,则∠PAB=3α,∠PDB=3β,
则有,
∴4∠P=3∠C+∠B,
∴∠P=(3x+y),
故答案为∠P=(3x+y).
(5)如图5中,延长AB交PD于J,设∠PBJ=x,∠ADP=∠PDE=y.
则有∠A+2x=∠C+180°﹣2y,
∴x+y=90°+(∠C﹣∠A),
∵∠P+x+∠A+y=180°,
∴∠P=90°﹣∠C﹣∠A.
故答案为∠P=90°﹣∠C﹣∠A.
一、选择题(本大题共10小题,每小题3分,共30分).
1.下列事物所运用的原理不属于三角形稳定性的是( )
A.长方形门框的斜拉条 B.埃及金字塔
C.三角形房架 D.学校的电动伸缩大门
2.已知三角形两边长分别为2cm和5cm,则该三角形第三边的长可能是( )
A.3cm B.6cm C.7cm D.9cm
3.如图,在△ABC中,BC边的高是( )
A.CE B.CD C.AC D.AF
4.如图所示,直线m∥n,直角三角形ABC(∠C=90°)的顶点A在直线n上,若∠β=43°,则∠α的度数为( )
A.47° B.43° C.57° D.53°
5.如图,点E、F分别在AB、CD上,∠B=40°,∠C=60°,则∠1+∠2等于( )
A.70° B.80° C.90° D.100°
6.在下列条件中,不能判定△ABC是直角三角形的是( )
A.3∠A=2∠B=∠C B.∠A+∠B=∠C
C.∠A=50°,∠B=40° D.∠A=∠B=∠C
7.将一副普通的直角三角尺ADE和ABC如图放置,点D恰好落在BC边上,三角尺中∠ABC=60°,较长的边AE∥BC,则∠FAD的度数是( )
A.30° B.25° C.10° D.15°
8.定义:当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么这个“特征角”α的度数为( )
A.48° B.96°
C.88°或48° D.48°或96°或88°
9.如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC; ②∠ACB=2∠ADB; ③DB平分∠ADC; ④∠ADC=90°﹣∠ABD; ⑤∠BDC=∠BAC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.如图,直线a∥b,Rt△ABC的直角顶点A落在直线a上,点B落在直线b上,若∠1=15°,∠2=25°,则∠ABC的大小为( )
A.40° B.45° C.50° D.55°
二、填空题(本大题共8小题,每小题3分,共24分)
11.内角和是1440°的多边形的边数是 .
12.如图△ABC中,AB=21,AC=20,AD为中线,则△ABD与△ACD的周长之差= .
13.如图,在四边形ABCD中,∠1=∠2=∠A=30°,则∠ADB= .
14.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,点D是AB延长线上一点,则∠CBD的度数是 .
15.如图,蚂蚁点P出发,沿直线行走40米后左转30°,再沿直线行走40米,又左转30°,…;照此走下去,它第一次回到出发点P,一共行走的路程是 米.
16.如图,将一副三角板和一支直尺按如图所示的位置摆放,则∠1的度数为 °.
17.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=15°,∠ACP=50°,则∠P= °.
18.如图,∠ABC=∠ACB,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC,以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠BAC+2∠BEC=180°.其中正确的结论有 .(填序号)
三、解答题(本大题共6小题,共46分.)
19.如图所示,已知AD是△ABC的边BC上的中线.
(1)作出△ABD的边BD上的高.
(2)若△ABC的面积为10,求△ADC的面积.
(3)若△ABD的面积为6,且BD边上的高为3,求BC的长.
20.如图,已知AD是△ABC的中线,∠B=33°,∠BAD=21°,△ABD的周长比△ADC的周长大2,且AB=5.
(1)求∠ADC的度数;
(2)求AC的长.
21.如图,△ABC中,D为BC上一点,∠C=∠BAD,△ABC的角平分线BE交AD于点F.
(1)求证:∠AEF=∠AFE;
(2)G为BC上一点,当FE平分∠AFG且∠C=30°时,求∠CGF的度数.
22.如图,∠CAD与∠CBD的角平分线交于点P.
(1)若∠C=35°,∠D=29°,求∠P的度数;
(2)猜想∠D,∠C,∠P的等量关系.
23.(1)如图1,在△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D,若∠ABC=75°,∠ACB=45°,求∠D的度数.
(2)如图2,在四边形MNCB中,BD平分∠MBC,且与四边形MNCB的外角∠NCE的角平分线交于点D,若∠BMN=130°,∠CNM=100°,求∠D的度数.
24.[问题背景]
(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B=∠C+∠D.
[简单应用](可直接使用问题(1)中的结论)
(2)如图2,AP、CP分别平分∠BAD、∠BCD,
①若∠ABC=28°,∠ADC=20°,求∠P的度数;
②∠D和∠B为任意角时,其他条件不变,试直接写出∠P与∠D、∠B之间数量关系.
[问题探究]
(3)如图3,直线BP平分∠ABC的邻补角∠FBC,DP平分∠ADC的邻补角∠ADE,
①若∠A=30°,∠C=18°,则∠P的度数为 ;
②∠A和∠C为任意角时,其他条件不变,试直接写出∠P与∠A、∠C之间数量关系.
[拓展延伸]
(4)在图4中,若设∠C=x,∠B=y,∠CAP=∠CAB,∠CDP=∠CDB,试问∠P与∠C、∠B之间的数量关系为 ;(用x、y的代数式表示∠P)
(5)在图5中,直线BP平分∠ABC,DP平分∠ADC的外角∠ADE,猜想∠P与∠A、∠C的关系,直接写出结论 .
答案
一、选择题
D.B.D.A.D.A.D.D.D.C.
二.填空题
11.10.
12.1.
13.120°.
14.140°.
15.480.
16.75.
17.35.
18.①②③④.
三.解答题
19.解:(1)如图所示:
(2)∵AD是△ABC的边BC上的中线,△ABC的面积为10,
∴△ADC的面积=△ABC的面积=5.
(3)∵AD是△ABC的边BC上的中线,△ABD的面积为6,
∴△ABC的面积为12,
∵BD边上的高为3,
∴BC=12×2÷3=8.
20.解:(1)∵∠B=33°,∠BAD=21°,∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=33°+21°=54°;
(2)∵AD是BC边上中线,
∴BD=CD,
∴△ABD的周长﹣△ADC的周长=AB﹣AC,
∵△ABD的周长比△ADC的周长大2,且AB=5.
∴5﹣AC=2,即AC=3.
21.解:(1)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABF+∠BAD=∠CBE+∠C,
∵∠AFE=∠ABF+∠BAD,∠AEF=∠CBE+∠C,
∴∠AEF=∠AFE;
(2)∵FE平分∠AFG,
∴∠AFE=∠GFE,
∵∠AEF=∠AFE,
∴∠AEF=∠GFE,
∴FG∥AC,
∵∠C=30°,
∴∠CGF=180°﹣∠C=150°.
22.解:(1)设∠CAD=2x,∠CBD=2y,
根据∠CAD和∠CBD的角平分线相交于点P可知:
∠CAP=∠PAD=x,∠CBP=∠DBP=y,
∵三角形的内角和等于180°,∠C=35°,∠D=29°,
∴∠C+∠CAD=∠D+∠CBD,即35°+2x=29°+2y①.
∵∠AEB是△APE与△DBE的外角,
∴∠P+∠EAP=∠D+∠DBP,即∠P+x=29°+y②.
同理,∵∠AFB是△ACF与△BFP的外角,
∴∠C+∠CAP=∠P+∠CBP,即35°+x=∠P+y③,
①﹣②得,y=x+35°﹣∠P④,
①﹣③得,x=y+29°﹣∠P⑤,
④代入⑤得,x=x+35°﹣∠P+29°﹣∠P,
2∠P=35°+29°,
解得∠P=32°;
(2)∠P=(∠C+∠D),理由如下:
由(1)同理可知:
2∠P=∠C+∠D,
解得∠P=(∠C+∠D).
23.解:(1)∵BD平分∠ABC,CD平分∠ACE,
∴,.
∵∠ACE=∠ABC+∠A,∠DCE=∠DBC+∠D,
∴=,即,
∴.
∵∠ABC=75°,∠ACB=45°,∠A=60°,
∴∠D=30°.
(2)如图,延长BM,CN交于点A.
∵∠BMN=∠ANM+∠A,∠CNM=∠AMN+∠A,
∴∠A=∠BMN+∠CNM﹣180°=50°,
由(1)知.
24.解:(1)如图1中,
∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)①如图2中,
设∠BAP=∠PAD=x,∠BCP=∠PCD=y,
则有,
∴∠B﹣∠P=∠P﹣∠D,
∴∠P=(∠B+∠D)=(28°+20°)=24°;
②2∠P=∠B+∠D;
(3)①如图3中,设∠CBJ=∠JBF=x,∠ADP=∠PDE=y.
则有,
∴2∠P=∠A+∠C,
∴∠P=(30°+18°)=24°;
故答案为:24°;
②设∠CBJ=∠JBF=x,∠ADP=∠PDE=y.
则有,
∴2∠P=∠A+∠C;
(4)如图4中,设∠CAP=α,∠CDP=β,则∠PAB=3α,∠PDB=3β,
则有,
∴4∠P=3∠C+∠B,
∴∠P=(3x+y),
故答案为∠P=(3x+y).
(5)如图5中,延长AB交PD于J,设∠PBJ=x,∠ADP=∠PDE=y.
则有∠A+2x=∠C+180°﹣2y,
∴x+y=90°+(∠C﹣∠A),
∵∠P+x+∠A+y=180°,
∴∠P=90°﹣∠C﹣∠A.
故答案为∠P=90°﹣∠C﹣∠A.
