2023-2024学年华师大版数学九年级上册 23.1.2 平行线分线段成比例 课件(共22张PPT)
文档属性
| 名称 | 2023-2024学年华师大版数学九年级上册 23.1.2 平行线分线段成比例 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 672.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 11:25:34 | ||
图片预览




文档简介
(共22张PPT)
23.1.2 平行线分线段成比例
教学目标
(1)了解相似三角形的概念.
(2)了解相似三角形与全等三角形之间的关系.
(3)掌握平行线分线段成比例的基本事实:
理解平行线分线段成比例定理的基本事实及其推论. (重点、难点)
教学重难点
一、温故知新
1.什么是成比例线段?判断四条线段成比例的步骤是什么?
2.比例的基本性质是什么?
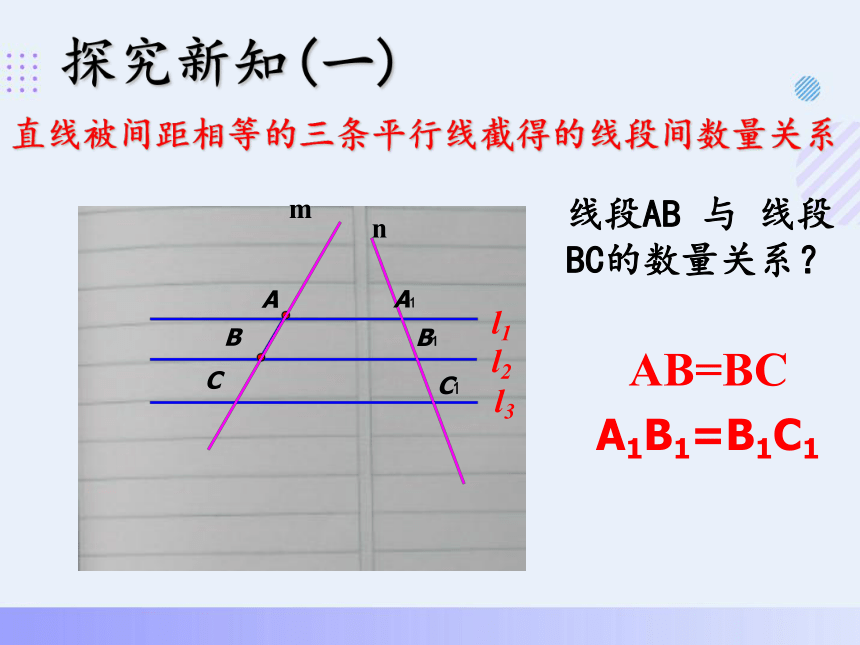
探究新知(一)
直线被间距相等的三条平行线截得的线段间数量关系
l1
l2
l3
A
B
C
线段AB 与 线段BC的数量关系?
AB=BC
A1
B1
C1
A1B1=B1C1
m
n
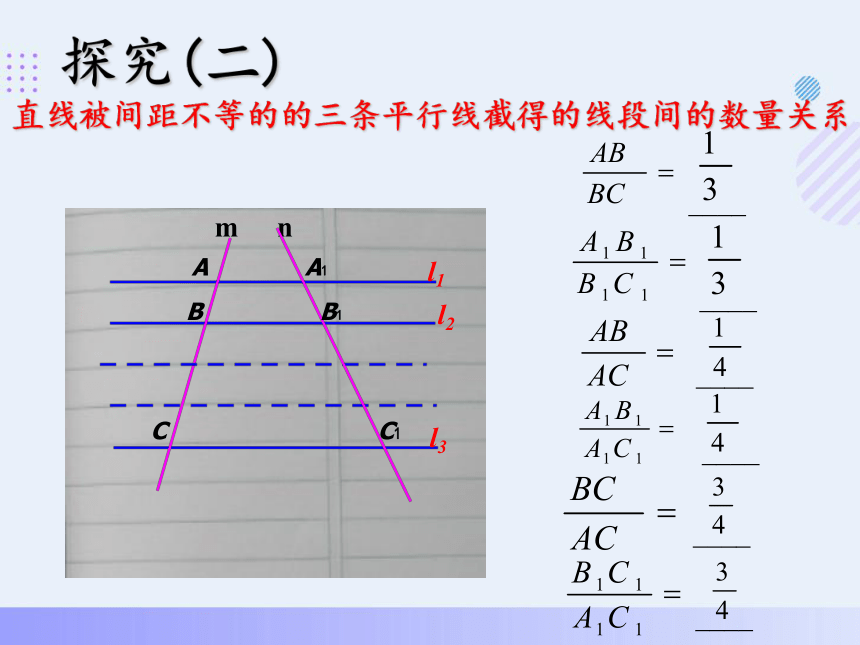
探究(二)
直线被间距不等的的三条平行线截得的线段间的数量关系
A
B
C
A1
B1
C1
l1
l2
l3
____
____
____
____
____
____
m
n
A
B
C
A1
B1
C1
l1
l2
l3
m
n
A
B
C
A1
B1
C1
l1
l2
l3
m
n
A
B
C
A1
B1
C1
l1
l2
l3
m
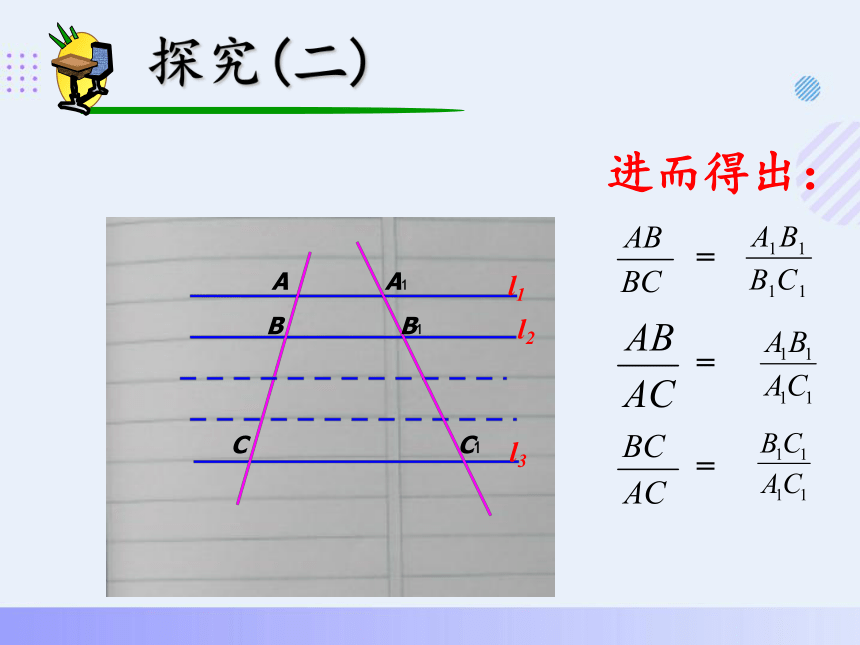
探究(二)
A
B
C
A1
B1
C1
l1
l2
l3
进而得出:
=
=
=
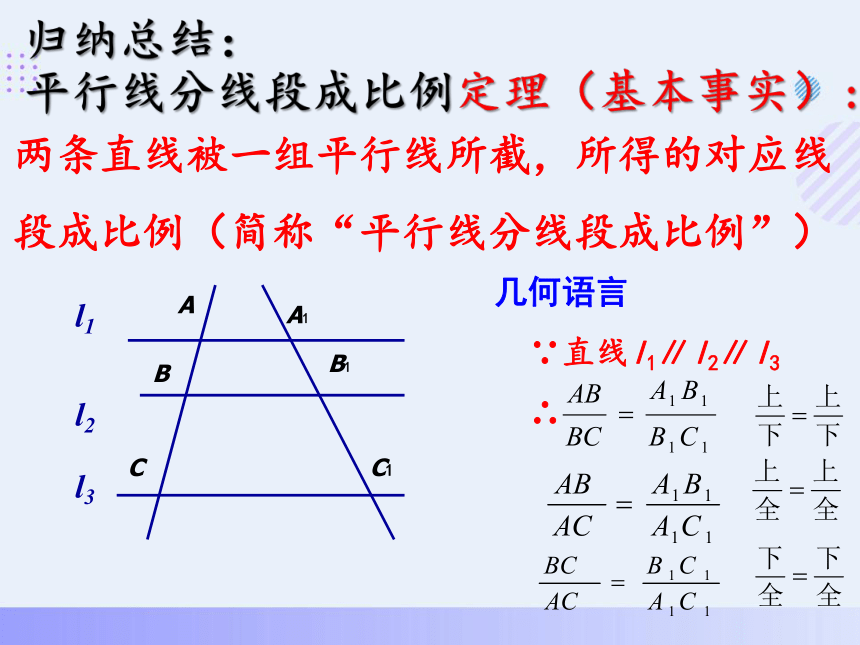
归纳总结:
平行线分线段成比例定理(基本事实):
几何语言
∵直线l1∥l2∥l3
∴
A
B
C
A1
B1
C1
l1
l2
l3
两条直线被一组平行线所截,所得的对应线
段成比例(简称“平行线分线段成比例”)
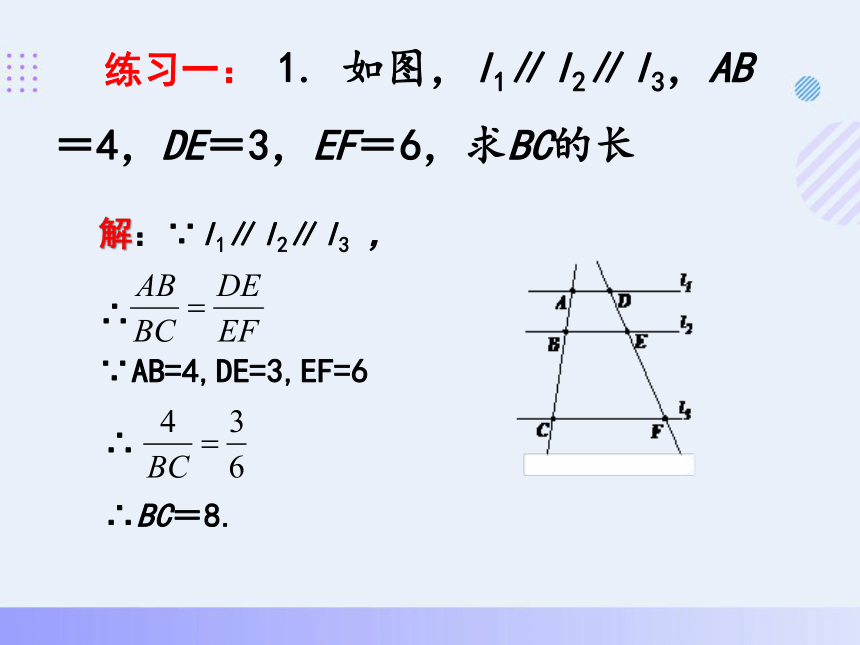
练习一: 1. 如图,l1∥l2∥l3,AB=4,DE=3,EF=6,求BC的长
解:∵l1∥l2∥l3 ,
∴
∵AB=4,DE=3,EF=6
∴
∴BC=8.
l1
l2
l3
m
n
A
D
B
C
E
F
n
仔细思考
几何语言
A
B
C
D
E
∵DE∥BC,
A型图
l1
l2
l3
m
n
D
A
B
C
F
E
n
∵DE∥BC,
几何语言
A
B
C
E
D
X型图
平行线分三角形两边成比例:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
几何语言:
∵ DE∥BC,
A
B
C
D
E
A
B
C
E
D
1、判断题:
如图:DE∥BC, 下列各式是否正确:
A
B
C
D
E
2、填空题:
如图:DE∥BC,已知 则
A
B
C
E
D
练习二:
做一做 教材p53
已知:DE//AF//BC,找出图中成比例的线段。
课堂小结
一、平行线分线段成比例基本事实:
两条直线被一组平行线所截,所得的对应线段成比例。(关键要能熟练地找出对应线段)
二、该基本事实在三角形中的应用:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
1.定理名称:
2.文字语言:
3.图形语言:
4.符号语言:
5.模型语言:
A
D
E
B
C
F
A
D
B
C
字母 型 字母 型
图4
图5
平行线分线段成比例定理的推论或三角形一边平行线的性质定理
平行于三角形一边的直线截其它两边(或两边的延长线),所得的对应线段成比例。
若DE∥BC 若AF∥BC
则: 则:
A
X
作业:
1.完成课本P54读一读;
2.课本P55练习题1,2题。
补充练习
1.已知:点E在平行四边形ABCD的边AB的延长线上,DE分别交AC、BC于点F、G,在图中找出字母A型图、字母X型图。
A
B
E
D
C
G
F
图10
答案
字母A型图
字母X型图
A
B
C
D
E
F
G
A
B
C
D
E
F
G
A
B
D
C
E
F
G
图10-1
图10-3
图10-4
图10-2
A
D
B
C
F
G
E
再见
23.1.2 平行线分线段成比例
教学目标
(1)了解相似三角形的概念.
(2)了解相似三角形与全等三角形之间的关系.
(3)掌握平行线分线段成比例的基本事实:
理解平行线分线段成比例定理的基本事实及其推论. (重点、难点)
教学重难点
一、温故知新
1.什么是成比例线段?判断四条线段成比例的步骤是什么?
2.比例的基本性质是什么?
探究新知(一)
直线被间距相等的三条平行线截得的线段间数量关系
l1
l2
l3
A
B
C
线段AB 与 线段BC的数量关系?
AB=BC
A1
B1
C1
A1B1=B1C1
m
n
探究(二)
直线被间距不等的的三条平行线截得的线段间的数量关系
A
B
C
A1
B1
C1
l1
l2
l3
____
____
____
____
____
____
m
n
A
B
C
A1
B1
C1
l1
l2
l3
m
n
A
B
C
A1
B1
C1
l1
l2
l3
m
n
A
B
C
A1
B1
C1
l1
l2
l3
m
探究(二)
A
B
C
A1
B1
C1
l1
l2
l3
进而得出:
=
=
=
归纳总结:
平行线分线段成比例定理(基本事实):
几何语言
∵直线l1∥l2∥l3
∴
A
B
C
A1
B1
C1
l1
l2
l3
两条直线被一组平行线所截,所得的对应线
段成比例(简称“平行线分线段成比例”)
练习一: 1. 如图,l1∥l2∥l3,AB=4,DE=3,EF=6,求BC的长
解:∵l1∥l2∥l3 ,
∴
∵AB=4,DE=3,EF=6
∴
∴BC=8.
l1
l2
l3
m
n
A
D
B
C
E
F
n
仔细思考
几何语言
A
B
C
D
E
∵DE∥BC,
A型图
l1
l2
l3
m
n
D
A
B
C
F
E
n
∵DE∥BC,
几何语言
A
B
C
E
D
X型图
平行线分三角形两边成比例:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
几何语言:
∵ DE∥BC,
A
B
C
D
E
A
B
C
E
D
1、判断题:
如图:DE∥BC, 下列各式是否正确:
A
B
C
D
E
2、填空题:
如图:DE∥BC,已知 则
A
B
C
E
D
练习二:
做一做 教材p53
已知:DE//AF//BC,找出图中成比例的线段。
课堂小结
一、平行线分线段成比例基本事实:
两条直线被一组平行线所截,所得的对应线段成比例。(关键要能熟练地找出对应线段)
二、该基本事实在三角形中的应用:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
1.定理名称:
2.文字语言:
3.图形语言:
4.符号语言:
5.模型语言:
A
D
E
B
C
F
A
D
B
C
字母 型 字母 型
图4
图5
平行线分线段成比例定理的推论或三角形一边平行线的性质定理
平行于三角形一边的直线截其它两边(或两边的延长线),所得的对应线段成比例。
若DE∥BC 若AF∥BC
则: 则:
A
X
作业:
1.完成课本P54读一读;
2.课本P55练习题1,2题。
补充练习
1.已知:点E在平行四边形ABCD的边AB的延长线上,DE分别交AC、BC于点F、G,在图中找出字母A型图、字母X型图。
A
B
E
D
C
G
F
图10
答案
字母A型图
字母X型图
A
B
C
D
E
F
G
A
B
C
D
E
F
G
A
B
D
C
E
F
G
图10-1
图10-3
图10-4
图10-2
A
D
B
C
F
G
E
再见
