2023-2024学年华师大版数学九年级上册 23.3.2 相似三角形的判定 课件(共22张PPT)
文档属性
| 名称 | 2023-2024学年华师大版数学九年级上册 23.3.2 相似三角形的判定 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 11:37:31 | ||
图片预览




文档简介
(共22张PPT)
23.3.2 相似三角形的判定
教学目标
1、经历两个三角形相似条件的探索过程,知道三角形相似的判定定理1,进一步体会类比、分类、归纳等思想与方法;
2.能应用相似三角形的判定定理1进行判定,进一步发展学生的合情推理能力和初步的逻辑推理能力。
自学内容:阅读教材第64页---65页内容. 自学方法:独立看书。 自学时间:4分钟。 自学要求:
1.思考第64页图中问题,并按要求完成第65页“探索”。
2.自学后完成学习检测。
A
B
C
D
E
F
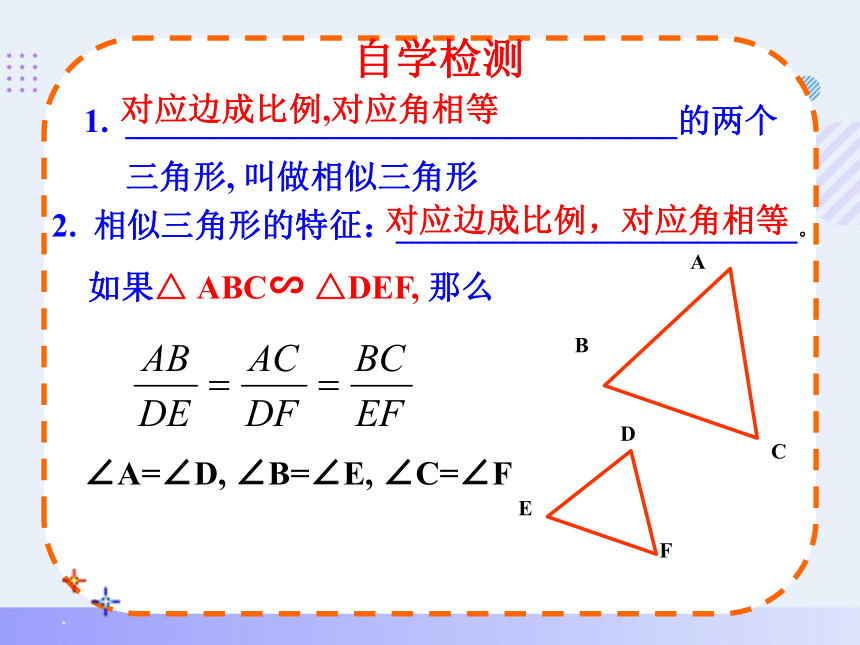
自学检测
1. _________________________________的两个
三角形, 叫做相似三角形
对应边成比例,对应角相等
2. 相似三角形的特征:________________________。
对应边成比例,对应角相等
如果△ ABC∽ △DEF, 那么
∠A=∠D, ∠B=∠E, ∠C=∠F
A′
B′
C′
10
6
12
51°
82°
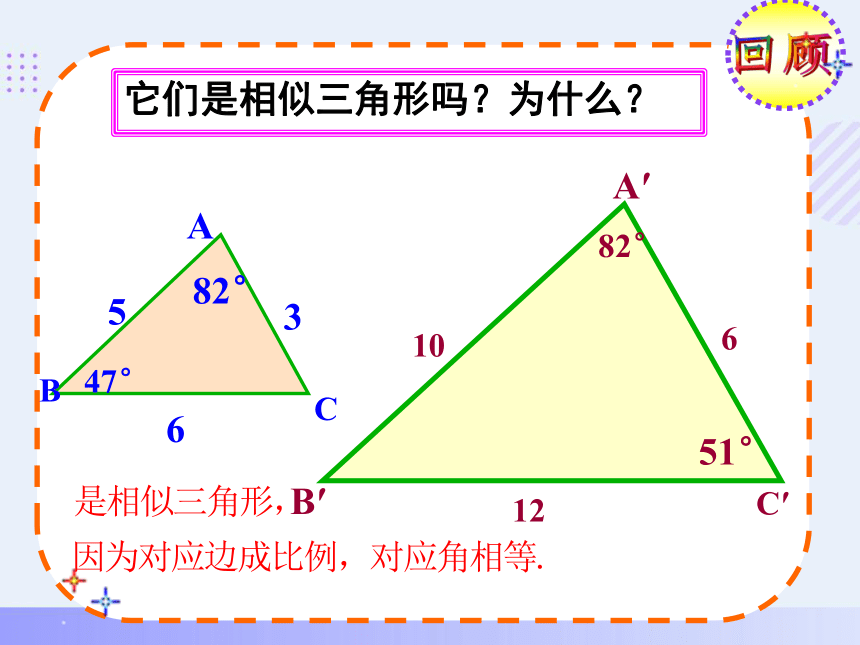
它们是相似三角形吗?为什么?
A
6
B
C
5
3
82°
47°
6
我们现在判定两个三角形是否相似,必须要知道它们的对应角是否相等,对应边是否成比例.那么是否存在判定两个三角形相似的简便方法呢?
观察你与你同伴的直角三角尺,同样角度(30°与60°,或45°与45°)的三角尺看起来是相似的.这样从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了.确实这样吗?
我们在判断两个三角形全等时,使用了哪些方法?判断三角形相似是否有类似的方法呢?
如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么它们相似吗?
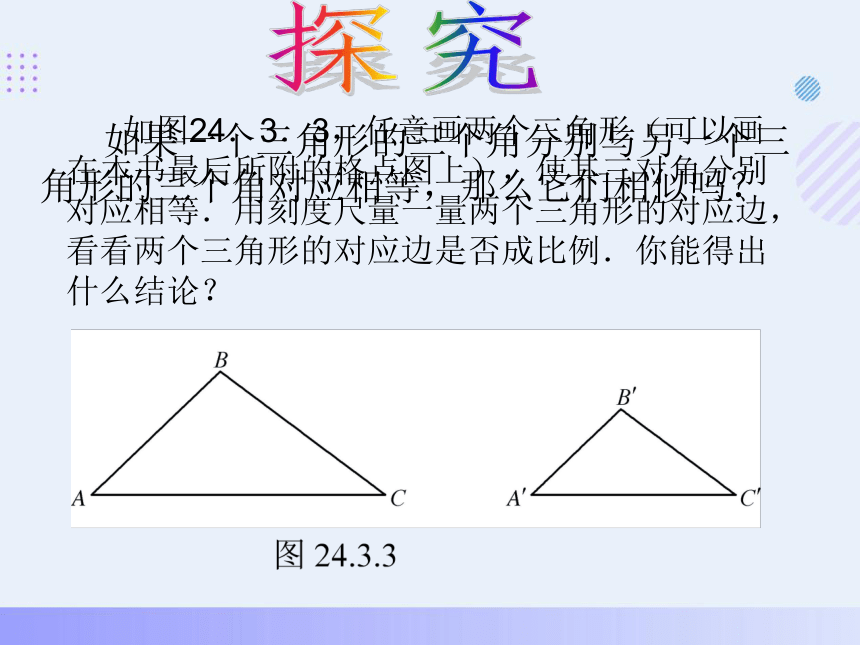
如图24.3.3,任意画两个三角形(可以画在本书最后所附的格点图上),使其三对角分别对应相等.用刻度尺量一量两个三角形的对应边,看看两个三角形的对应边是否成比例.你能得出什么结论?
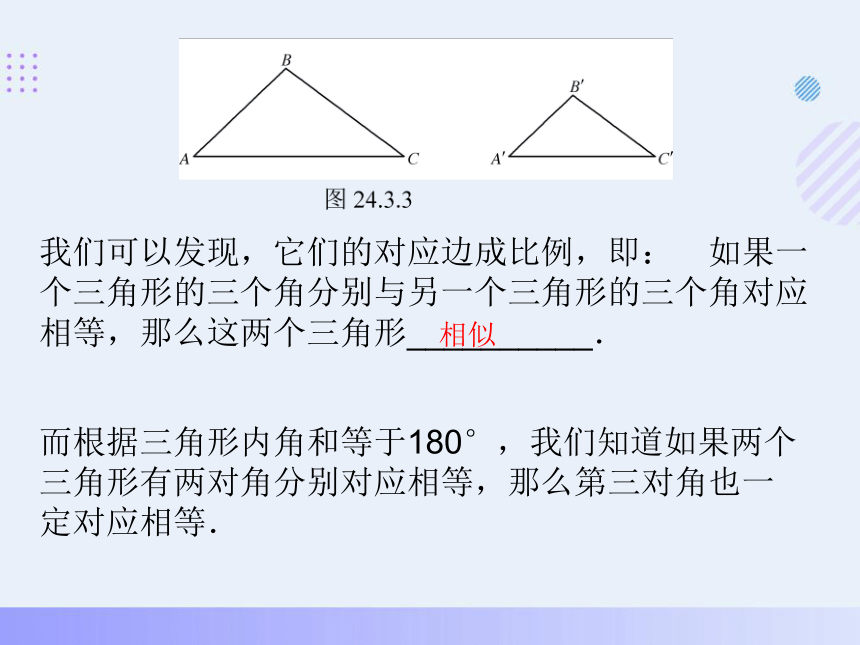
我们可以发现,它们的对应边成比例,即: 如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形__________.
而根据三角形内角和等于180°,我们知道如果两个三角形有两对角分别对应相等,那么第三对角也一定对应相等.
相似
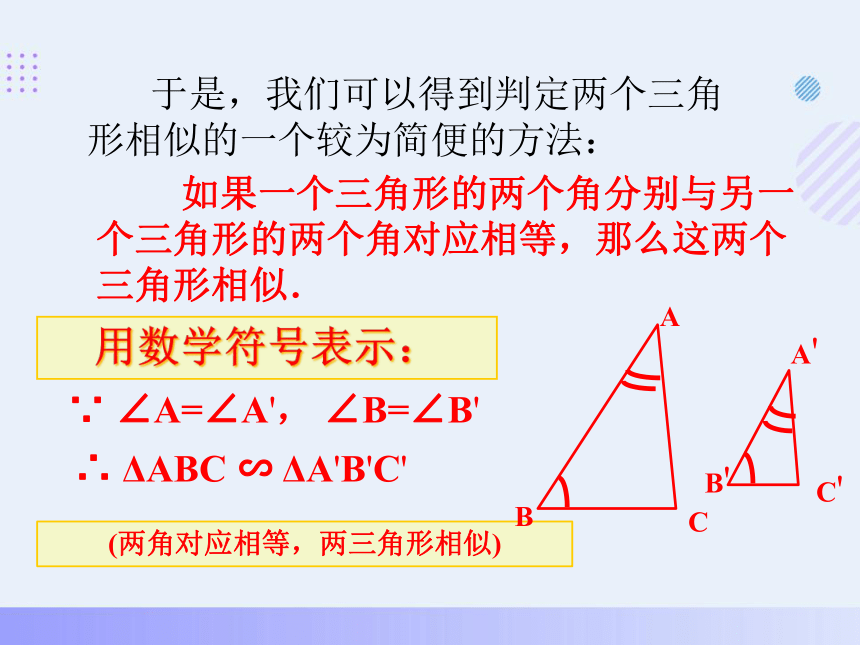
于是,我们可以得到判定两个三角形相似的一个较为简便的方法:
如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似.
用数学符号表示:
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
(两角对应相等,两三角形相似)
B
C
A
A'
B'
C'
C
A
思考
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
1.下列各组图形可能不相似的是( )
(A)有一个角是60°的两个等腰三角形
(B)各有一个角是45°的两个等腰三角形
(C)各有一个角是105°的两个等腰三角形
(D)两个等腰直角三角形
2 .如图AD⊥BC于D,CE⊥AB于E交AD于F,则图中相似三角形的对数有几对 请分别写出来?
3. 已知:如图,在△ABC中,∠AED=∠B,则下列等式成立的是( )
B
6对它们分别是△AEF∽△ADB∽△CEB∽△CDF
C
自学内容:教材第66页---67页内容. 自学方法:独立看书。 自学时间:5分钟。 自学要求:
1.思考第66页云图中内容、并按要求完成“想一想”。
2.自学后完成学习检测。
1 如图24.3.4所示,在两个直角三角形△ABC和△A′B′C′中,∠C=∠C′=90°,∠A=∠A′,证明△ABC∽△A′B′C′.
证明 ∵ ∠C=∠C′=90°,
∠A=∠A′,
∴ △ABC∽△A′B′C′(如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似).
如图,△ABC中,DE∥BC,EF∥AB,证明: △ADE∽△EFC.
证明 ∵ DE∥BC,EF∥AB,
∴ ∠ADE=∠B=∠EFC,
∴ ∠AED=∠C,
∴ △ADE∽△EFC(如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似).
如果点D恰好是边AB的中点,那么点E是边AC的中点吗?DE和BC又有什么关系呢?
1.(1)两个等边三角形相似( )
(2)两个直角三角形相似( )
(3)两个等腰直角三角形相似( )
(4)有一个角为50°的两个等腰三角形相似( )
(5)有一个角为100°的两个等腰三角形相似( )
2.如图, ABCD中,E是CD的延长线上一点,BE与AD交于点F.求证:△ABF∽△CEB.
3.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.
√
×
√
×
√
<
<
1. 如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____
2.已知在△ABC和△DEF中, ∠A=40°,∠B=80°,∠E=80°, ∠F=60°求证:△ABC∽△DEF.
.
1:4
3. 如图,Rt△ABC中,CD是斜边上的高,找出图中相似的三角形?写出各对应的成比例线段,并证明你的结论
<
<
4.已知:如图,在△ABC中,DE∥BC,DE分别
与AB、AC相交于D、E,AD∶AB=1∶3.
若DE=2,则BC=
5.已知△ABC∽△DEF,BG、EH分别是△ABC和△DEF的角平分线,BC=6 cm,EF=4 cm,BG=4.8 cm.求EH的长.
6
3.2cm
三等角模型
如图,△ABC中,AB=AC,D是BC上
一点,且∠ABC=∠ADE=∠ACB找出图中相似的三角形,并写出其对应成比例的线段
A
B
C
D
E
△ABD∽DCE
AB:DC=BD:CE=AD:DE
三直角模型
如图,AB⊥BC,AE⊥DE,DC⊥BC,找出图中相似的三角形,并写出比例线段
A
B
C
D
E
△ABC∽ECD
AB:EC=BC:CD=AC:ED
通过本节课的学习,你有哪些收获?
教材第75页4(1)、76页5.
23.3.2 相似三角形的判定
教学目标
1、经历两个三角形相似条件的探索过程,知道三角形相似的判定定理1,进一步体会类比、分类、归纳等思想与方法;
2.能应用相似三角形的判定定理1进行判定,进一步发展学生的合情推理能力和初步的逻辑推理能力。
自学内容:阅读教材第64页---65页内容. 自学方法:独立看书。 自学时间:4分钟。 自学要求:
1.思考第64页图中问题,并按要求完成第65页“探索”。
2.自学后完成学习检测。
A
B
C
D
E
F
自学检测
1. _________________________________的两个
三角形, 叫做相似三角形
对应边成比例,对应角相等
2. 相似三角形的特征:________________________。
对应边成比例,对应角相等
如果△ ABC∽ △DEF, 那么
∠A=∠D, ∠B=∠E, ∠C=∠F
A′
B′
C′
10
6
12
51°
82°
它们是相似三角形吗?为什么?
A
6
B
C
5
3
82°
47°
6
我们现在判定两个三角形是否相似,必须要知道它们的对应角是否相等,对应边是否成比例.那么是否存在判定两个三角形相似的简便方法呢?
观察你与你同伴的直角三角尺,同样角度(30°与60°,或45°与45°)的三角尺看起来是相似的.这样从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了.确实这样吗?
我们在判断两个三角形全等时,使用了哪些方法?判断三角形相似是否有类似的方法呢?
如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么它们相似吗?
如图24.3.3,任意画两个三角形(可以画在本书最后所附的格点图上),使其三对角分别对应相等.用刻度尺量一量两个三角形的对应边,看看两个三角形的对应边是否成比例.你能得出什么结论?
我们可以发现,它们的对应边成比例,即: 如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形__________.
而根据三角形内角和等于180°,我们知道如果两个三角形有两对角分别对应相等,那么第三对角也一定对应相等.
相似
于是,我们可以得到判定两个三角形相似的一个较为简便的方法:
如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似.
用数学符号表示:
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
(两角对应相等,两三角形相似)
B
C
A
A'
B'
C'
C
A
思考
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
1.下列各组图形可能不相似的是( )
(A)有一个角是60°的两个等腰三角形
(B)各有一个角是45°的两个等腰三角形
(C)各有一个角是105°的两个等腰三角形
(D)两个等腰直角三角形
2 .如图AD⊥BC于D,CE⊥AB于E交AD于F,则图中相似三角形的对数有几对 请分别写出来?
3. 已知:如图,在△ABC中,∠AED=∠B,则下列等式成立的是( )
B
6对它们分别是△AEF∽△ADB∽△CEB∽△CDF
C
自学内容:教材第66页---67页内容. 自学方法:独立看书。 自学时间:5分钟。 自学要求:
1.思考第66页云图中内容、并按要求完成“想一想”。
2.自学后完成学习检测。
1 如图24.3.4所示,在两个直角三角形△ABC和△A′B′C′中,∠C=∠C′=90°,∠A=∠A′,证明△ABC∽△A′B′C′.
证明 ∵ ∠C=∠C′=90°,
∠A=∠A′,
∴ △ABC∽△A′B′C′(如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似).
如图,△ABC中,DE∥BC,EF∥AB,证明: △ADE∽△EFC.
证明 ∵ DE∥BC,EF∥AB,
∴ ∠ADE=∠B=∠EFC,
∴ ∠AED=∠C,
∴ △ADE∽△EFC(如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似).
如果点D恰好是边AB的中点,那么点E是边AC的中点吗?DE和BC又有什么关系呢?
1.(1)两个等边三角形相似( )
(2)两个直角三角形相似( )
(3)两个等腰直角三角形相似( )
(4)有一个角为50°的两个等腰三角形相似( )
(5)有一个角为100°的两个等腰三角形相似( )
2.如图, ABCD中,E是CD的延长线上一点,BE与AD交于点F.求证:△ABF∽△CEB.
3.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.
√
×
√
×
√
<
<
1. 如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____
2.已知在△ABC和△DEF中, ∠A=40°,∠B=80°,∠E=80°, ∠F=60°求证:△ABC∽△DEF.
.
1:4
3. 如图,Rt△ABC中,CD是斜边上的高,找出图中相似的三角形?写出各对应的成比例线段,并证明你的结论
<
<
4.已知:如图,在△ABC中,DE∥BC,DE分别
与AB、AC相交于D、E,AD∶AB=1∶3.
若DE=2,则BC=
5.已知△ABC∽△DEF,BG、EH分别是△ABC和△DEF的角平分线,BC=6 cm,EF=4 cm,BG=4.8 cm.求EH的长.
6
3.2cm
三等角模型
如图,△ABC中,AB=AC,D是BC上
一点,且∠ABC=∠ADE=∠ACB找出图中相似的三角形,并写出其对应成比例的线段
A
B
C
D
E
△ABD∽DCE
AB:DC=BD:CE=AD:DE
三直角模型
如图,AB⊥BC,AE⊥DE,DC⊥BC,找出图中相似的三角形,并写出比例线段
A
B
C
D
E
△ABC∽ECD
AB:EC=BC:CD=AC:ED
通过本节课的学习,你有哪些收获?
教材第75页4(1)、76页5.
