2014-2015学年高二上学期苏教版数学期末模拟试卷
文档属性
| 名称 | 2014-2015学年高二上学期苏教版数学期末模拟试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 348.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-06 15:19:42 | ||
图片预览



文档简介
2014-2015学年高中数学苏教版期末模拟试卷 必修三
评卷人
得分
一、选择题(题型注释)
1.某单位有840名职工, 现采用系统抽样方法, 抽取42人做问卷调查, 将840人按1, 2,…840随机编号, 则抽取的42人中, 编号落入区间[481, 720]的人数为( )
A.11 B.12 C.13 D.14
2.袋中有大小相同的黄、红、白球各一个,每次任取一个,有放回地取3次,则是下列哪个是事件的概率 ( )【版权所有:21教育】
A.颜色全同 B.颜色全不同 C.颜色不全同 D.无红球
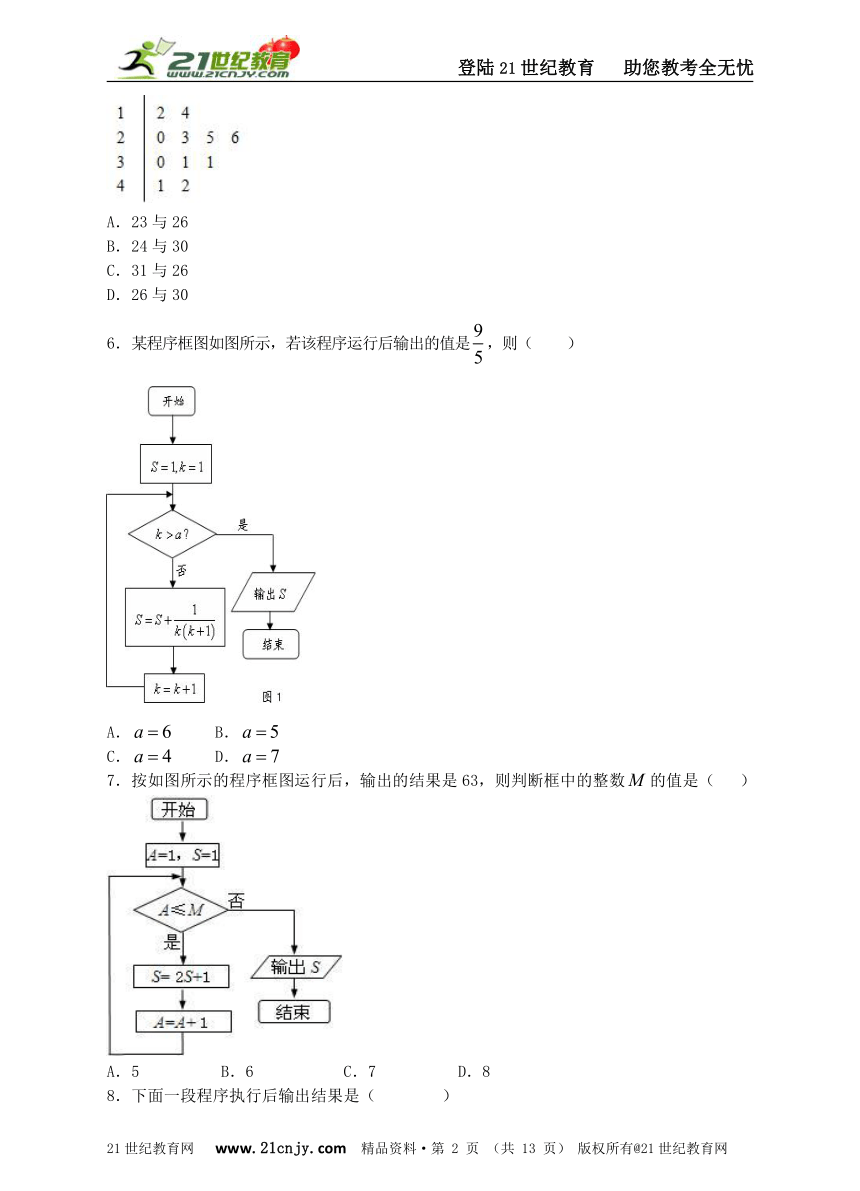
3. 某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为,若低于60分的人数是15人,则该班的学生人数是( )
A. B. C. D.
4.如图所示,程序框图(算法流程图)的输出结果是 ( )
A. B. C. D.
5.在如图所示的“茎叶图”表示的数据中,众数和中位数分别( )
A.23与26
B.24与30
C.31与26
D.26与30
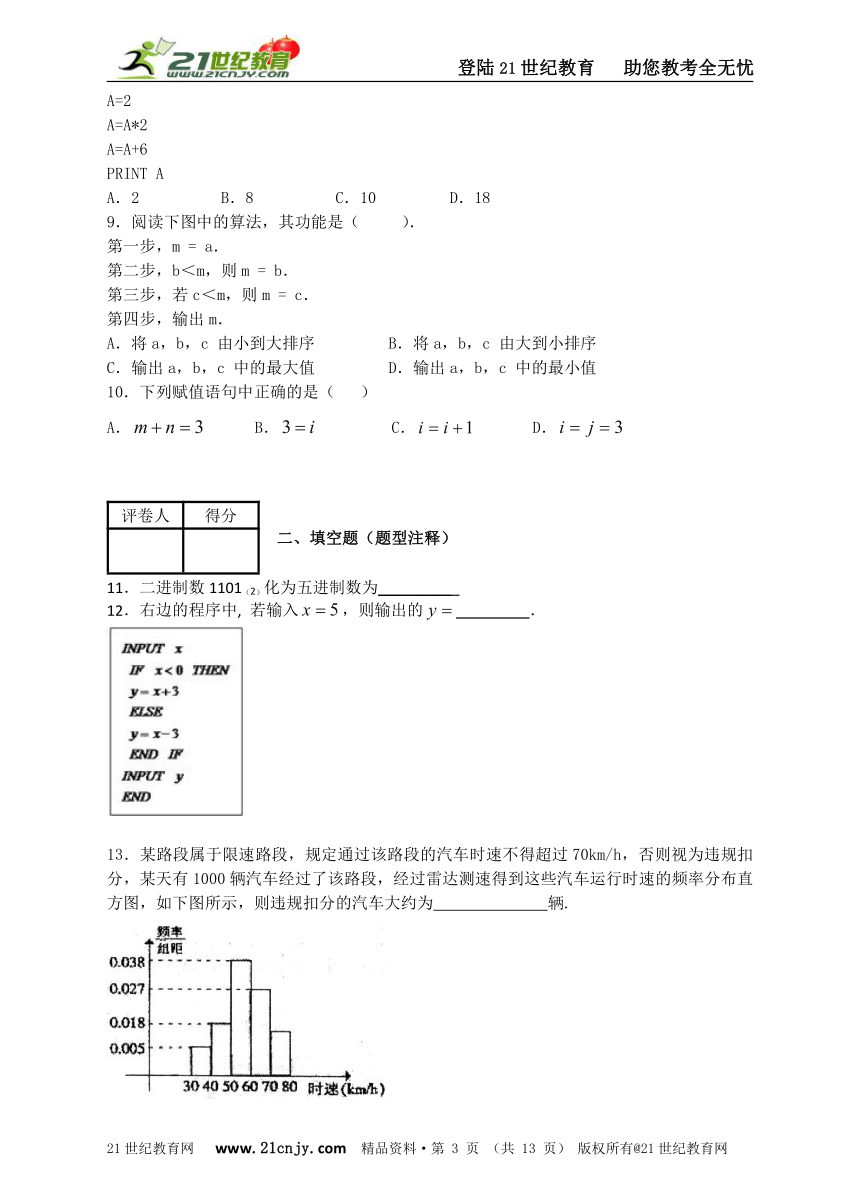
6.某程序框图如图所示,若该程序运行后输出的值是,则( )
A. B.
C. D.
7.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数的值是( )
A.5 B.6 C.7 D.8
8.下面一段程序执行后输出结果是( )
A=2
A=A*2
A=A+6
PRINT A
A.2 B.8 C.10 D.18
9.阅读下图中的算法,其功能是( ).
第一步,m = a.
第二步,b<m,则m = b.
第三步,若c<m,则m = c.
第四步,输出m.
A.将a,b,c 由小到大排序 B.将a,b,c 由大到小排序
C.输出a,b,c 中的最大值 D.输出a,b,c 中的最小值
10.下列赋值语句中正确的是( )
A. B. C. D.
评卷人
得分
二、填空题(题型注释)
11.二进制数1101(2)化为五进制数为_________
12.右边的程序中, 若输入,则输出的 .
13.某路段属于限速路段,规定通过该路段的汽车时速不得超过70km/h,否则视为违规扣分,某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图,如下图所示,则违规扣分的汽车大约为 辆.21·cn·jy·com
14.已知点E在正△ABC的边AB上,AE = 2EB,在边AC上任意取一点P,则“△AEP的面积恰好小于△ABC面积的一半”的概率为 .【来源:21·世纪·教育·网】
15.在区间[-6,6]内任取一个元素x0,抛物线x2=4y在x=x0处的切线的倾斜角为α,则α∈[,]的概率为________.21·世纪*教育网www-2-1-cnjy-com
16.若不等式组表示的平面区域为M,x2+y2≤1所表示的平面区域为N,现随机向区域M内抛一粒豆子,则豆子落在区域N内的概率为________.
17.张先生订了一份《南昌晚报》,送报人在早上6:30-7:30之间把报纸送到他家,张先生离开家去上班的时间在早上7:00-8:00之间,则张先生在离开家之前能拿到报纸的概率是________.www-2-1-cnjy-com【出处:21教育名师】
18.有一个底面圆的半径为1、高为2的圆柱,点O为这个圆柱底面圆的圆心,在这个圆柱内随机取一点P,则点P到点O的距离大于1的概率为________.21*cnjy*com
19.某校早上8:00开始上课,假设该校学生小张与小王在早上7:30—7:50之间到校,且每人在
该时间段的任何时刻到校是等可能的,则小张比小王至少早5分钟到校的概率为_____(用数字作答)
20.某校有高中学生2000人,其中高三学生800人,高一学生的人数与高二学生人数之比为,为了解高中学生身体素质,采用分层抽样,共抽取一个100人的样本,则样本中高一学生人数为__ ____人.21教育网 21*cnjy*com
评卷人
得分
三、解答题
21.(本小题满分13分)图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是 .【来源:21·世纪·教育·网】
(1)从正方形ABCD的四条边及两条对角线共6条线段中任取2条线段(每条线段被取到的可能性相等),求其中一条线段长度是另一条线段长度的倍的概率;
(2)求此长方体的体积.
22.(本小题满分13分)如图是学校从走读生中随机调查200名走读生早上上学所需时间(单位:分钟)样本的频率分布直方图.
(1)学校所有走读生早上上学所需要的平均时间约是多少分钟?
(2)根据调查,距离学校500米以内的走读生上学时间不超过10分钟,距离学校1000米以内的走读生上学时间不超过20分钟.那么,距离学校500米以内的走读生和距离学校1000米以上的走读生所占全校走读生的百分率各是多少?
23.(本小题满分12分)下图是调查某地某公司1000名员工的月收入后制作的直方图.
(1)求该公司员工的月平均收入及员工月收入的中位数;
(2)在收入为1000至1500元和收入为3500至4000元的员工中用分层抽样的方法抽取一个容量15的样本, 员工甲、乙的月收入分别为1200元、3800元, 求甲乙同时被抽到的概率.
24.(满分12分)某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60), ,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:
(1)求第四小组的频率;并补全频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分。
参考答案
1.B
【解析】
试题分析:经分析,组距为20,计算所以编号落入区间[481, 720]的人数为12人。
考点:样本数据的频率分布。
2.C
【解析】
试题分析:所有可能的情况如下:黄红白,黄白红,红黄白,红白黄,白黄红,白红黄,黄黄红,黄红黄,红黄黄,黄黄白,黄白黄,白黄黄,红红白,红白红,白红红,红红黄,红黄红,黄红红,白白黄,白黄白,黄白白,白白红,白红白,白红白,黄黄黄,红红红,白白白,则颜色全同的概率为颜色全不同的概率为,颜色不全同的概率为无红球的概率为,故选C。21世纪教育网版权所有21世纪教育网版权所有
考点:有放回的抽样概率。
3.B
【解析】
试题分析:从频率分布直方图分析可知,低于60分包括
的频率为(0.005+0.01)20=0.3,因此该班的学生人数为。
考点:从频率分布直方图求频率。
4.D
【解析】
试题分析:经分析当时,退出循环结构 ,输出
考点:1、程序框图的认识;2、循环结构。
5.C
【解析】
试题分析:通过分析茎叶图中的数据为12、14、20、23、25、26、30、31、31、41、42,其众数和中位数分别为31与26。21cnjy.com21·世纪*教育网
考点:1、对茎叶图的认识;2、众数、中位数。
6.C
【解析】第一次,S=1,k=1,进入循环,S=
第二次,k=2,再进入循环,S=
第三次,k=3,再进入循环,S=
第四次,k=4,再进入循环,S=
第五次,k=5,跳出循环,故a=4
考点:算法,程序框图
7.A
【解析】
试题分析:第一次执行完循环体,,此时判断框的条件成立,第二次执行完循环体,
,此时判断框的条件成立,第三次执行完循环体,,此时判断框的条件成立,第四次执行完循环体,,此时判断框的条件成立,第五次执行完循环体,,此时判断框的条件不成立,,故答案为A.
考点:程序框图的应用.
8.C
【解析】
试题分析:第一步,把2赋值给A,则A=2
第二步,把赋值给A,则A=4
第三步,则把4+6赋值给A,则A=10
第四步,输出10.
考点:赋值语句.
9.D
【解析】
试题分析:第一步,把赋值给
第二步,若b<m,则把赋值给
第三步,若c<m,则把赋值给
第四步,输出的m为a,b,c 中的最小值.
考点:条件结构.
10.C
【解析】
试题分析:A:左侧为代数式,不是赋值语句;B:左侧为数字,不是赋值语句;C:赋值语句,把i+1的值赋给i;D:是等式,不是赋值语句.2·1·c·n·j·y21教育网
考点:赋值语句.
11.23
【解析】
试题分析:将二进制数转化为十进制数,再把十进制化为五进制.
1101(2)=1×23+1×22+1=13
13=2
考点:不同进制之间的转换
12.2
【解析】
试题分析:INPUT的意思就是输入一数,然后作出选择,IF即为假如输入的数小于0,THEN即则执行;ELSE即为假如输入的数大于或等于0时,执行,最后输出结果;本题输入的是,所以执行,即。
考点:基本算法语句、条件语句
13.120.
【解析】
试题分析:易求得70-80这组的频率为1-0.05-0.18-0.38-0.27=0.12,则违规扣分的汽车大约为辆.2-1-c-n-j-y21·cn·jy·com
考点:频率分布直方图中每组对应的长方形面积为,总面积为1,频数=频率样本容量.
14.
【解析】
试题分析:设AP=x,当△AEP的面积恰好等于于△ABC面积的一半时,
S△AEP= AE?x?sinA= S△ABC= ? AB?AC?sinA,
即?AB?x?sinA= ? AB?AC?sinA,解得x=AC,
故所求的概率P==
故答案为:
考点:几何概型.
15.
【解析】当切线的倾斜角α∈[,]时,切线斜率的取值范围是(-∞,-1]∪[1,+∞),抛物线x2=4y在x=x0处的切线斜率是x0,故只要x0∈(-∞,-2]∪[2,+∞)即可,若在区间[-6,6]内取值,则只能取区间[-6,-2]∪[2,6)内的值,这个区间的长度是8,区间[-6,6]的长度是12,故所求的概率是=.www.21-cn-jy.com21cnjy.com
16.
【解析】如图,△AOB为区域M,扇形COD为区域M内的区域N,易知A(3,3),B(1,-1),S△AOB=××3=3,S扇形COD=,所以豆子落在区域N内的概率为=.
17.
【解析】以横坐标x表示报纸送到时间,以纵坐标y表示张先生离家时间,建立平面直角坐标系,如图.因为随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.根据题意只要点落在阴影部分,就表示张先生在离开家之前能拿到报纸,即所求事件A发生,所以P(A)==. 21*cnjy*comwww.21-cn-jy.com
18.
【解析】先求点P到点O的距离小于或等于1的概率,圆柱的体积V圆柱=π×12×2=2π,以O为球心,1为半径且在圆柱内部的半球的体积V半球=×π×13=π.则点P到点O的距离小于或等于1的概率为=,故点P到点O的距离大于1的概率为1-=.
19.
【解析】
试题分析:用表示小张到校的时间,
用表示小王到校的时间,
则所有可能的结果对应直角坐标平面内的正方形区域
记“小张比小王至少早到5分钟”为事件M,则M所对区域为图中的阴影部分
所以
所以答案应填:.
考点:几何概型.
20.24
【解析】
试题分析:由题意得高一高二高三人数为480 ,720 ,800 三者的比为6:9:10 则样本中高一人数为人【来源:21cnj*y.co*m】2·1·c·n·j·y
考点:1.统计知识.2.分层抽样.
21.(1);(2).
【解析】
试题分析:(1)本题属于古典概型中的等可能性事件概率,依题意,用列举法可列出6条线段中任取2条线段的15种结果,而其中一条线段长度是另一条线段长度的倍,则说明一条线段取自正方形的边,另一线段取自正方形的对角线,可列举出共有8种结果,故概率为;(2)依题意设长方体的高为,则虚线框的面积为,而长方体的平面展开图的面积即为长方体的表面积为,由几何概型的概率公式知,从而,故长方体的体积是.【出处:21教育名师】
试题解析:(1)记事件:从6条线段中任取2条线段,其中一条线段长度是另一条线段长度的倍.从6条线段中任取2条线段,有15种等可能的取法:和, 和,和, 和,和,和,和,和,和,和,和, 和,和, 和,和 3分
其中事件包含8种结果:和,和,和,和,和,和,和, 和 4分21教育名师原创作品
,因此,所求事件的概率为 6分
(2)记事件:向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内.
设长方体的高为,则图2中虚线围成的矩形长为,宽为,面积为 9分
长方体的平面展开图的面积为; 10分
由几何概型的概率公式知,得, 12分
所以长方体的体积是. 13分
考点:两种概率类型的概率计算
22.(1); (2) 40﹪, 6﹪.
【解析】
试题分析:(1)本题考查由样本的频率分布直方图求样本数据的平均值,由图代入数据得; (2)距离学校500米以内的走读生分布在第一小组和第二小组,概率为=40%,从而可得各小组人数分别为16,64,72,24,24,故距离学校1000米以上的走读生人数为12,概率为6%.21*cnjy*com2-1-c-n-j-y
试题解析:(1),
所以,走读生早上上学所需要的平均时间约为分钟. 6分
(2)﹪,﹪, 12分
所以距离学校500米以内的走读生占全校走读生的40﹪,距离学校1000米以上的走读生占全校走读生的6﹪. 13分【来源:21cnj*y.co*m】
考点:由频率分布直方图求样本平均数和概率
23.(1)平均收入为2400,中位数为2400;
(2)甲、乙同时被抽到的概率为
【解析】
试题分析:
(1)利用组中值,可得该公司员工的月平均收入及员工月收入的中位数;
(2)月收入在1000至1500元之间的有100人,月收入在3500元至4000元之间的有50人,由分层抽样可知甲、乙同时被抽到的概率.【版权所有:21教育】
试题解析:(1)可求出第一个小矩形的高度为0.0002
平均收入为2400元
中位数为元(面积分为相等的两部分; (3分)
(2)月收入在1000至1500元之间的有100人, 月收入在3500元至4000元之间的有50人, 由分层抽样可知, 甲、乙同时被抽到的概率为21教育名师原创作品
考点:频率分布直方图
24.(1)第四小组的频率为0.3;频率分布直方图见解析.
(2)及格率 75%,平均分71.
【解析】
试题分析:(1)由图知,第一组、第二组、第三组、第五组、第六组的频率依次为0.1,0.15,0.15,0.25,0.05,而各组的频率和等于1,故可得第四组的频率为0.3,从而可画出对应的全频率分布直方图;
(2)60分及以上的分数所在的第三、四、五、六组的频率和为0.75,故及格率为75%;利用频率分布直方图求平均值得:平均分=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.
试题解析:
(1)因为各组的频率和等于1,故第四组的频率:
f4=1-(0.025+0.015×2+0.01+0.005)×10=0.3. (3分)
其频率分布直方图如图所示. (5分)
(2)依题意,60分及以上的分数所在的第三、四、五、六组,频率和为:
(0.015+0.030+0.025+0.005)×10=0.75.
所以,估计这次考试的合格率是75%. (8分)
利用组中值估算这次考试的平均分,可得:
45·f1+55·f2+65·f3+75·f4+85·f5+95·f6 (10分)
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71 (12分)
考点:统计的有关计算
评卷人
得分
一、选择题(题型注释)
1.某单位有840名职工, 现采用系统抽样方法, 抽取42人做问卷调查, 将840人按1, 2,…840随机编号, 则抽取的42人中, 编号落入区间[481, 720]的人数为( )
A.11 B.12 C.13 D.14
2.袋中有大小相同的黄、红、白球各一个,每次任取一个,有放回地取3次,则是下列哪个是事件的概率 ( )【版权所有:21教育】
A.颜色全同 B.颜色全不同 C.颜色不全同 D.无红球
3. 某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为,若低于60分的人数是15人,则该班的学生人数是( )
A. B. C. D.
4.如图所示,程序框图(算法流程图)的输出结果是 ( )
A. B. C. D.
5.在如图所示的“茎叶图”表示的数据中,众数和中位数分别( )
A.23与26
B.24与30
C.31与26
D.26与30
6.某程序框图如图所示,若该程序运行后输出的值是,则( )
A. B.
C. D.
7.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数的值是( )
A.5 B.6 C.7 D.8
8.下面一段程序执行后输出结果是( )
A=2
A=A*2
A=A+6
PRINT A
A.2 B.8 C.10 D.18
9.阅读下图中的算法,其功能是( ).
第一步,m = a.
第二步,b<m,则m = b.
第三步,若c<m,则m = c.
第四步,输出m.
A.将a,b,c 由小到大排序 B.将a,b,c 由大到小排序
C.输出a,b,c 中的最大值 D.输出a,b,c 中的最小值
10.下列赋值语句中正确的是( )
A. B. C. D.
评卷人
得分
二、填空题(题型注释)
11.二进制数1101(2)化为五进制数为_________
12.右边的程序中, 若输入,则输出的 .
13.某路段属于限速路段,规定通过该路段的汽车时速不得超过70km/h,否则视为违规扣分,某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图,如下图所示,则违规扣分的汽车大约为 辆.21·cn·jy·com
14.已知点E在正△ABC的边AB上,AE = 2EB,在边AC上任意取一点P,则“△AEP的面积恰好小于△ABC面积的一半”的概率为 .【来源:21·世纪·教育·网】
15.在区间[-6,6]内任取一个元素x0,抛物线x2=4y在x=x0处的切线的倾斜角为α,则α∈[,]的概率为________.21·世纪*教育网www-2-1-cnjy-com
16.若不等式组表示的平面区域为M,x2+y2≤1所表示的平面区域为N,现随机向区域M内抛一粒豆子,则豆子落在区域N内的概率为________.
17.张先生订了一份《南昌晚报》,送报人在早上6:30-7:30之间把报纸送到他家,张先生离开家去上班的时间在早上7:00-8:00之间,则张先生在离开家之前能拿到报纸的概率是________.www-2-1-cnjy-com【出处:21教育名师】
18.有一个底面圆的半径为1、高为2的圆柱,点O为这个圆柱底面圆的圆心,在这个圆柱内随机取一点P,则点P到点O的距离大于1的概率为________.21*cnjy*com
19.某校早上8:00开始上课,假设该校学生小张与小王在早上7:30—7:50之间到校,且每人在
该时间段的任何时刻到校是等可能的,则小张比小王至少早5分钟到校的概率为_____(用数字作答)
20.某校有高中学生2000人,其中高三学生800人,高一学生的人数与高二学生人数之比为,为了解高中学生身体素质,采用分层抽样,共抽取一个100人的样本,则样本中高一学生人数为__ ____人.21教育网 21*cnjy*com
评卷人
得分
三、解答题
21.(本小题满分13分)图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是 .【来源:21·世纪·教育·网】
(1)从正方形ABCD的四条边及两条对角线共6条线段中任取2条线段(每条线段被取到的可能性相等),求其中一条线段长度是另一条线段长度的倍的概率;
(2)求此长方体的体积.
22.(本小题满分13分)如图是学校从走读生中随机调查200名走读生早上上学所需时间(单位:分钟)样本的频率分布直方图.
(1)学校所有走读生早上上学所需要的平均时间约是多少分钟?
(2)根据调查,距离学校500米以内的走读生上学时间不超过10分钟,距离学校1000米以内的走读生上学时间不超过20分钟.那么,距离学校500米以内的走读生和距离学校1000米以上的走读生所占全校走读生的百分率各是多少?
23.(本小题满分12分)下图是调查某地某公司1000名员工的月收入后制作的直方图.
(1)求该公司员工的月平均收入及员工月收入的中位数;
(2)在收入为1000至1500元和收入为3500至4000元的员工中用分层抽样的方法抽取一个容量15的样本, 员工甲、乙的月收入分别为1200元、3800元, 求甲乙同时被抽到的概率.
24.(满分12分)某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60), ,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:
(1)求第四小组的频率;并补全频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分。
参考答案
1.B
【解析】
试题分析:经分析,组距为20,计算所以编号落入区间[481, 720]的人数为12人。
考点:样本数据的频率分布。
2.C
【解析】
试题分析:所有可能的情况如下:黄红白,黄白红,红黄白,红白黄,白黄红,白红黄,黄黄红,黄红黄,红黄黄,黄黄白,黄白黄,白黄黄,红红白,红白红,白红红,红红黄,红黄红,黄红红,白白黄,白黄白,黄白白,白白红,白红白,白红白,黄黄黄,红红红,白白白,则颜色全同的概率为颜色全不同的概率为,颜色不全同的概率为无红球的概率为,故选C。21世纪教育网版权所有21世纪教育网版权所有
考点:有放回的抽样概率。
3.B
【解析】
试题分析:从频率分布直方图分析可知,低于60分包括
的频率为(0.005+0.01)20=0.3,因此该班的学生人数为。
考点:从频率分布直方图求频率。
4.D
【解析】
试题分析:经分析当时,退出循环结构 ,输出
考点:1、程序框图的认识;2、循环结构。
5.C
【解析】
试题分析:通过分析茎叶图中的数据为12、14、20、23、25、26、30、31、31、41、42,其众数和中位数分别为31与26。21cnjy.com21·世纪*教育网
考点:1、对茎叶图的认识;2、众数、中位数。
6.C
【解析】第一次,S=1,k=1,进入循环,S=
第二次,k=2,再进入循环,S=
第三次,k=3,再进入循环,S=
第四次,k=4,再进入循环,S=
第五次,k=5,跳出循环,故a=4
考点:算法,程序框图
7.A
【解析】
试题分析:第一次执行完循环体,,此时判断框的条件成立,第二次执行完循环体,
,此时判断框的条件成立,第三次执行完循环体,,此时判断框的条件成立,第四次执行完循环体,,此时判断框的条件成立,第五次执行完循环体,,此时判断框的条件不成立,,故答案为A.
考点:程序框图的应用.
8.C
【解析】
试题分析:第一步,把2赋值给A,则A=2
第二步,把赋值给A,则A=4
第三步,则把4+6赋值给A,则A=10
第四步,输出10.
考点:赋值语句.
9.D
【解析】
试题分析:第一步,把赋值给
第二步,若b<m,则把赋值给
第三步,若c<m,则把赋值给
第四步,输出的m为a,b,c 中的最小值.
考点:条件结构.
10.C
【解析】
试题分析:A:左侧为代数式,不是赋值语句;B:左侧为数字,不是赋值语句;C:赋值语句,把i+1的值赋给i;D:是等式,不是赋值语句.2·1·c·n·j·y21教育网
考点:赋值语句.
11.23
【解析】
试题分析:将二进制数转化为十进制数,再把十进制化为五进制.
1101(2)=1×23+1×22+1=13
13=2
考点:不同进制之间的转换
12.2
【解析】
试题分析:INPUT的意思就是输入一数,然后作出选择,IF即为假如输入的数小于0,THEN即则执行;ELSE即为假如输入的数大于或等于0时,执行,最后输出结果;本题输入的是,所以执行,即。
考点:基本算法语句、条件语句
13.120.
【解析】
试题分析:易求得70-80这组的频率为1-0.05-0.18-0.38-0.27=0.12,则违规扣分的汽车大约为辆.2-1-c-n-j-y21·cn·jy·com
考点:频率分布直方图中每组对应的长方形面积为,总面积为1,频数=频率样本容量.
14.
【解析】
试题分析:设AP=x,当△AEP的面积恰好等于于△ABC面积的一半时,
S△AEP= AE?x?sinA= S△ABC= ? AB?AC?sinA,
即?AB?x?sinA= ? AB?AC?sinA,解得x=AC,
故所求的概率P==
故答案为:
考点:几何概型.
15.
【解析】当切线的倾斜角α∈[,]时,切线斜率的取值范围是(-∞,-1]∪[1,+∞),抛物线x2=4y在x=x0处的切线斜率是x0,故只要x0∈(-∞,-2]∪[2,+∞)即可,若在区间[-6,6]内取值,则只能取区间[-6,-2]∪[2,6)内的值,这个区间的长度是8,区间[-6,6]的长度是12,故所求的概率是=.www.21-cn-jy.com21cnjy.com
16.
【解析】如图,△AOB为区域M,扇形COD为区域M内的区域N,易知A(3,3),B(1,-1),S△AOB=××3=3,S扇形COD=,所以豆子落在区域N内的概率为=.
17.
【解析】以横坐标x表示报纸送到时间,以纵坐标y表示张先生离家时间,建立平面直角坐标系,如图.因为随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.根据题意只要点落在阴影部分,就表示张先生在离开家之前能拿到报纸,即所求事件A发生,所以P(A)==. 21*cnjy*comwww.21-cn-jy.com
18.
【解析】先求点P到点O的距离小于或等于1的概率,圆柱的体积V圆柱=π×12×2=2π,以O为球心,1为半径且在圆柱内部的半球的体积V半球=×π×13=π.则点P到点O的距离小于或等于1的概率为=,故点P到点O的距离大于1的概率为1-=.
19.
【解析】
试题分析:用表示小张到校的时间,
用表示小王到校的时间,
则所有可能的结果对应直角坐标平面内的正方形区域
记“小张比小王至少早到5分钟”为事件M,则M所对区域为图中的阴影部分
所以
所以答案应填:.
考点:几何概型.
20.24
【解析】
试题分析:由题意得高一高二高三人数为480 ,720 ,800 三者的比为6:9:10 则样本中高一人数为人【来源:21cnj*y.co*m】2·1·c·n·j·y
考点:1.统计知识.2.分层抽样.
21.(1);(2).
【解析】
试题分析:(1)本题属于古典概型中的等可能性事件概率,依题意,用列举法可列出6条线段中任取2条线段的15种结果,而其中一条线段长度是另一条线段长度的倍,则说明一条线段取自正方形的边,另一线段取自正方形的对角线,可列举出共有8种结果,故概率为;(2)依题意设长方体的高为,则虚线框的面积为,而长方体的平面展开图的面积即为长方体的表面积为,由几何概型的概率公式知,从而,故长方体的体积是.【出处:21教育名师】
试题解析:(1)记事件:从6条线段中任取2条线段,其中一条线段长度是另一条线段长度的倍.从6条线段中任取2条线段,有15种等可能的取法:和, 和,和, 和,和,和,和,和,和,和,和, 和,和, 和,和 3分
其中事件包含8种结果:和,和,和,和,和,和,和, 和 4分21教育名师原创作品
,因此,所求事件的概率为 6分
(2)记事件:向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内.
设长方体的高为,则图2中虚线围成的矩形长为,宽为,面积为 9分
长方体的平面展开图的面积为; 10分
由几何概型的概率公式知,得, 12分
所以长方体的体积是. 13分
考点:两种概率类型的概率计算
22.(1); (2) 40﹪, 6﹪.
【解析】
试题分析:(1)本题考查由样本的频率分布直方图求样本数据的平均值,由图代入数据得; (2)距离学校500米以内的走读生分布在第一小组和第二小组,概率为=40%,从而可得各小组人数分别为16,64,72,24,24,故距离学校1000米以上的走读生人数为12,概率为6%.21*cnjy*com2-1-c-n-j-y
试题解析:(1),
所以,走读生早上上学所需要的平均时间约为分钟. 6分
(2)﹪,﹪, 12分
所以距离学校500米以内的走读生占全校走读生的40﹪,距离学校1000米以上的走读生占全校走读生的6﹪. 13分【来源:21cnj*y.co*m】
考点:由频率分布直方图求样本平均数和概率
23.(1)平均收入为2400,中位数为2400;
(2)甲、乙同时被抽到的概率为
【解析】
试题分析:
(1)利用组中值,可得该公司员工的月平均收入及员工月收入的中位数;
(2)月收入在1000至1500元之间的有100人,月收入在3500元至4000元之间的有50人,由分层抽样可知甲、乙同时被抽到的概率.【版权所有:21教育】
试题解析:(1)可求出第一个小矩形的高度为0.0002
平均收入为2400元
中位数为元(面积分为相等的两部分; (3分)
(2)月收入在1000至1500元之间的有100人, 月收入在3500元至4000元之间的有50人, 由分层抽样可知, 甲、乙同时被抽到的概率为21教育名师原创作品
考点:频率分布直方图
24.(1)第四小组的频率为0.3;频率分布直方图见解析.
(2)及格率 75%,平均分71.
【解析】
试题分析:(1)由图知,第一组、第二组、第三组、第五组、第六组的频率依次为0.1,0.15,0.15,0.25,0.05,而各组的频率和等于1,故可得第四组的频率为0.3,从而可画出对应的全频率分布直方图;
(2)60分及以上的分数所在的第三、四、五、六组的频率和为0.75,故及格率为75%;利用频率分布直方图求平均值得:平均分=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.
试题解析:
(1)因为各组的频率和等于1,故第四组的频率:
f4=1-(0.025+0.015×2+0.01+0.005)×10=0.3. (3分)
其频率分布直方图如图所示. (5分)
(2)依题意,60分及以上的分数所在的第三、四、五、六组,频率和为:
(0.015+0.030+0.025+0.005)×10=0.75.
所以,估计这次考试的合格率是75%. (8分)
利用组中值估算这次考试的平均分,可得:
45·f1+55·f2+65·f3+75·f4+85·f5+95·f6 (10分)
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71 (12分)
考点:统计的有关计算
同课章节目录
