2. 圆的对称性(2)(广东省深圳市)
文档属性
| 名称 | 2. 圆的对称性(2)(广东省深圳市) |  | |
| 格式 | rar | ||
| 文件大小 | 488.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-01-08 10:09:00 | ||
图片预览

文档简介
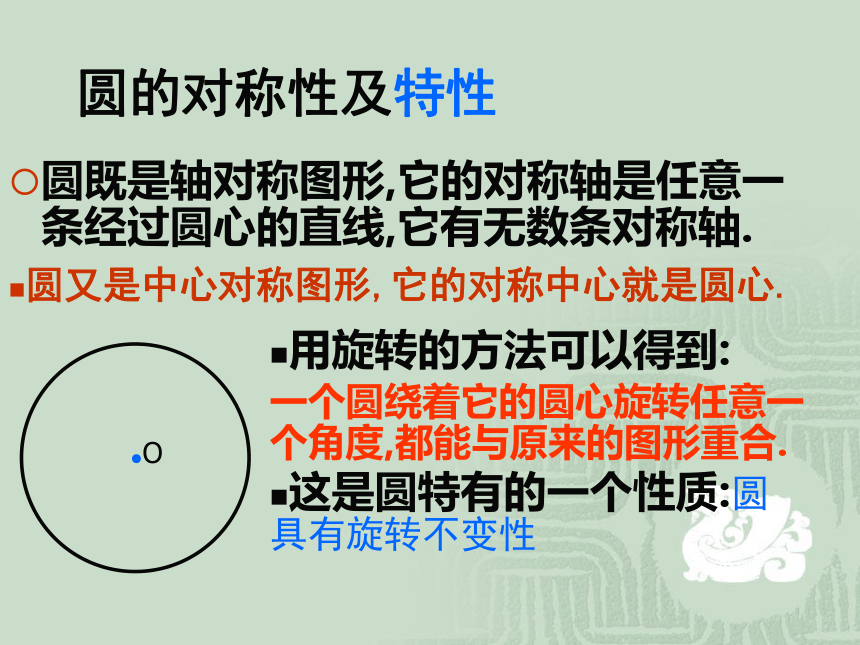
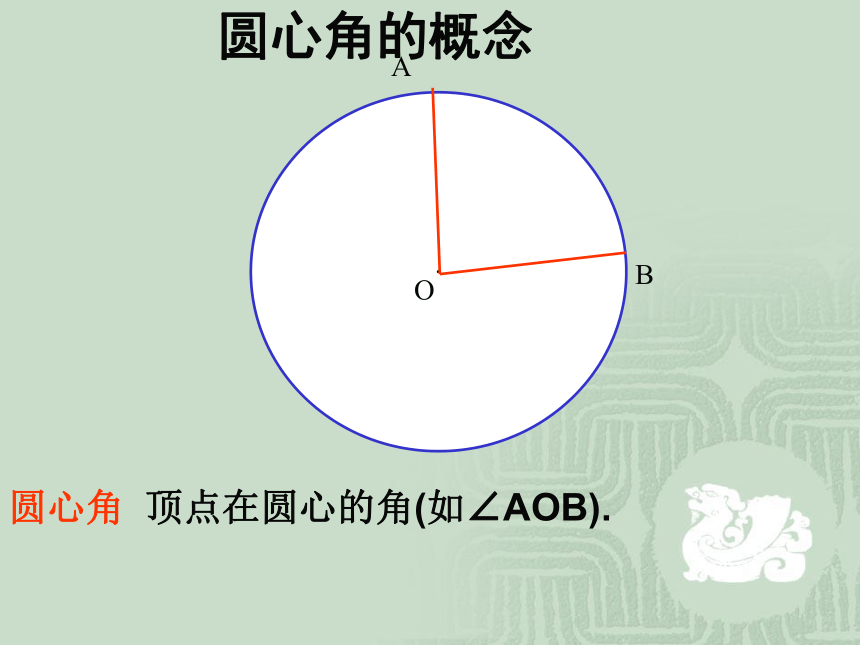
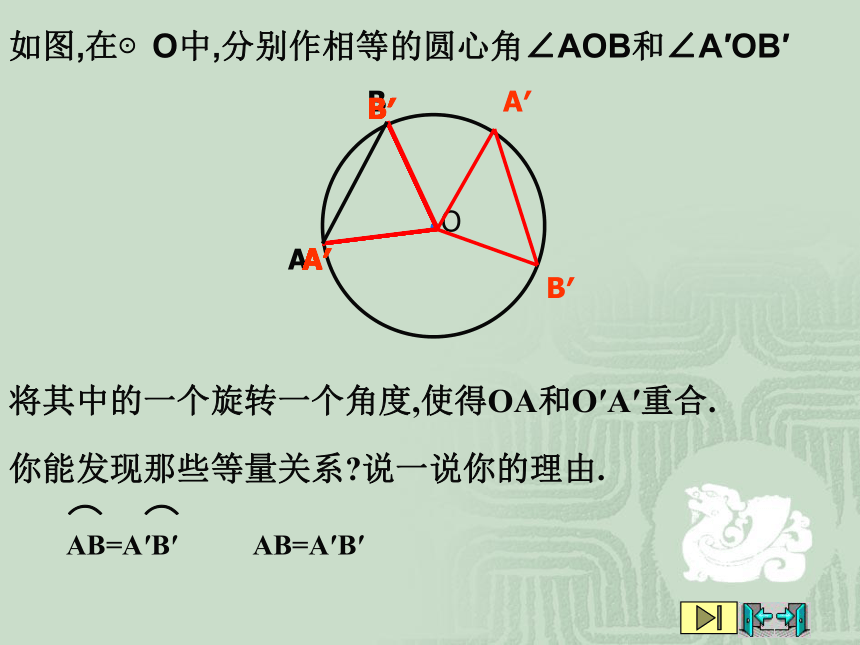
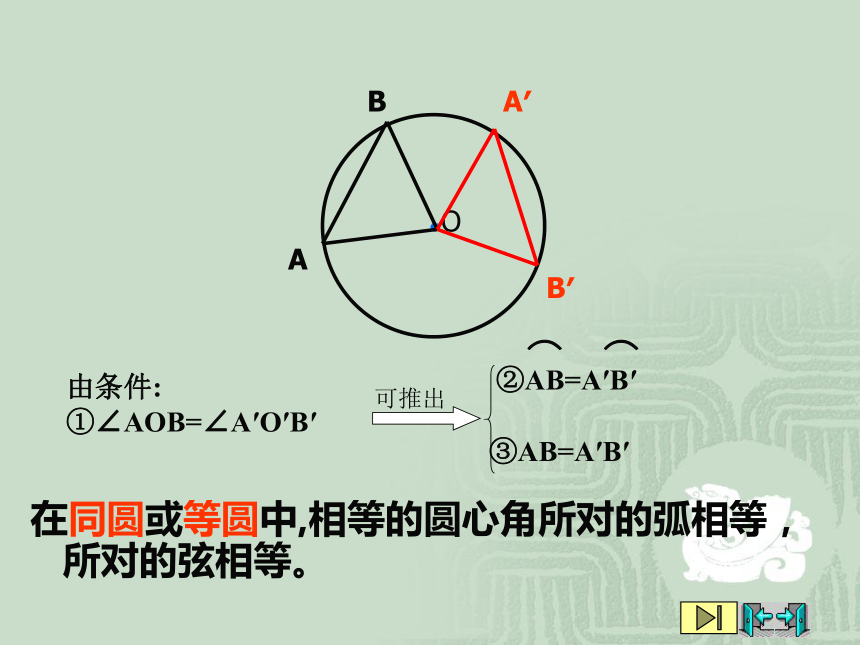
课件21张PPT。2. 圆的对称性(2)圆心角,弧,弦,弦心距之间的关系九年级数下学期 北师大版(1)圆是中心对称图形吗?(2)如果是,它的对称中心是什么?圆也是中心对称图形.它的对称中心就是圆心.圆的对称性及特性圆既是轴对称图形,它的对称轴是任意一条经过圆心的直线,它有无数条对称轴.圆又是中心对称图形,它的对称中心就是圆心.用旋转的方法可以得到:一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆具有旋转不变性圆心角 顶点在圆心的角(如∠AOB).圆心角的概念如图,在⊙O中,分别作相等的圆心角∠AOB和∠A′OB′你能发现那些等量关系?说一说你的理由.将其中的一个旋转一个角度,使得OA和O′A′重合.
由条件:
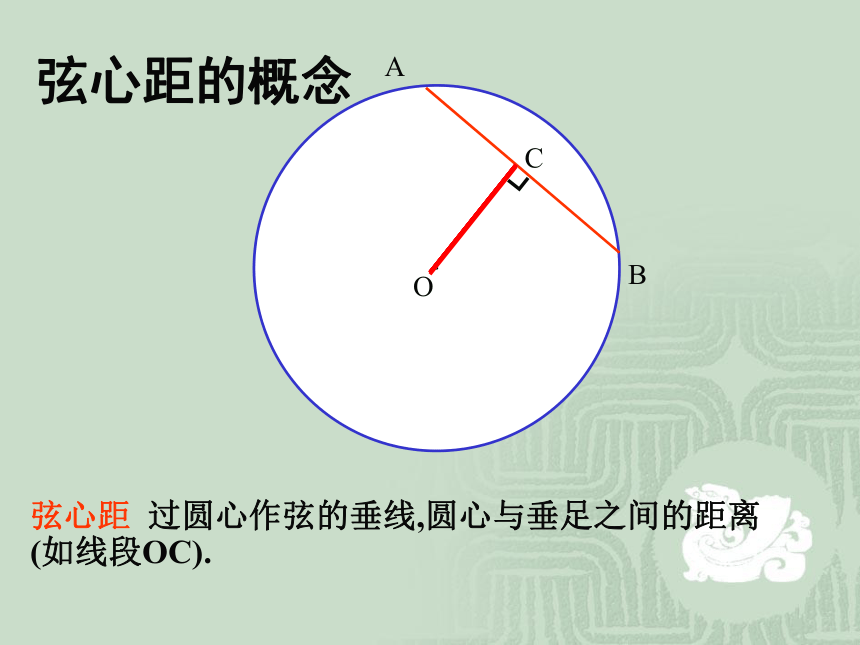
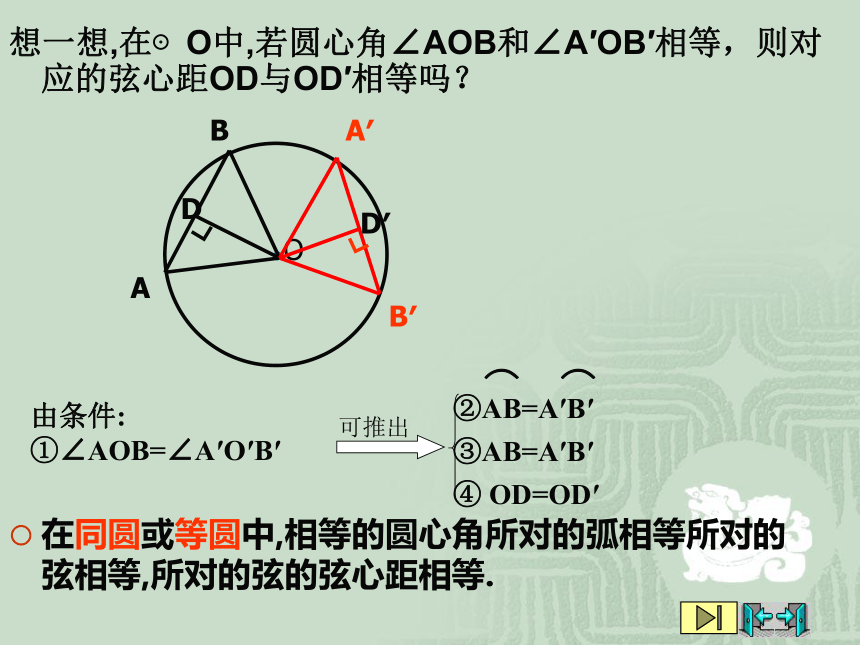
①∠AOB=∠A′O′B′③AB=A′B′在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。弦心距的概念弦心距 过圆心作弦的垂线,圆心与垂足之间的距离(如线段OC).想一想,在⊙O中,若圆心角∠AOB和∠A′OB′相等,则对应的弦心距OD与OD′相等吗?由条件:
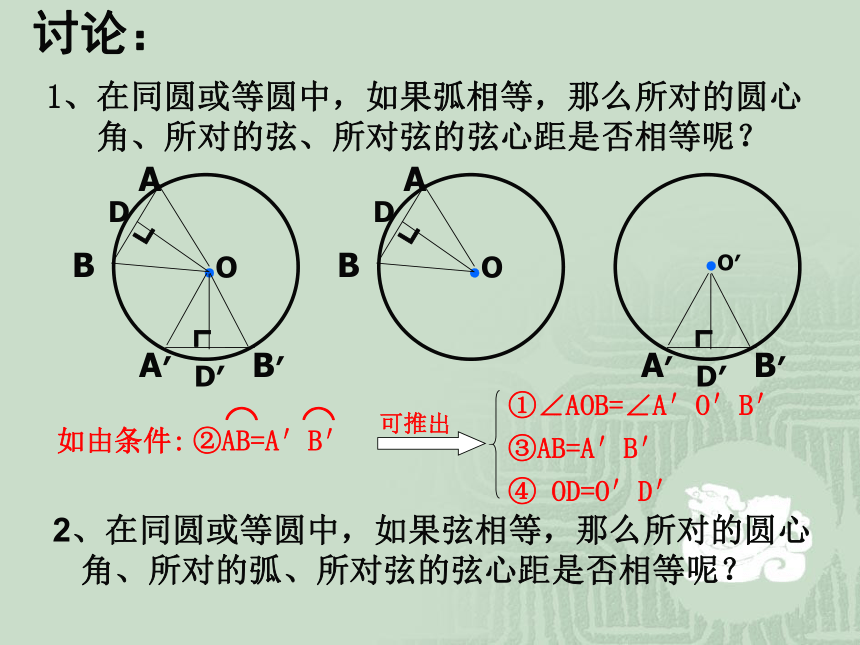
①∠AOB=∠A′O′B′③AB=A′B′④ OD=OD′在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.讨论:1、在同圆或等圆中,如果弧相等,那么所对的圆心
角、所对的弦、所对弦的弦心距是否相等呢?2、在同圆或等圆中,如果弦相等,那么所对的圆心
角、所对的弧、所对弦的弦心距是否相等呢?如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等. 抢答题
已知:如图,AB,CD是⊙O的两条弦,
OE,OF为AB、CD的弦心距,根据这
节课所学的定理及推论填空:ABCFDEO(2)如果OE=OF,那么 , , ;(4)如果AB=CD,那么 , , 。(1)如果∠AOB=∠COD,那么 , , ;∠AOB=∠COD AB=CD OE=OF试一试你的能力 3、如图,在⊙O中,弧AC=弧BD,
求∠2的度数。4、下面的说法正确吗?为什么?如图,因为
根据圆心角、弧、弦、弦心距的关系定理
可知: 试一试你的能力抢答题试一试你的能力5.判断下列说法是否正确:
相等的圆心角所对的弧相等。( )
6.如图,⊙O中,AB=CD,
,则×7、在⊙O中,a、b为弦,他们
的弦心距分别为 c、d,若a>b,则( )
A c<d B c>d
C c=d D 无法确定8、已知A、B是⊙O上的两点∠AOB=120°, C是弧AB的中点,试确定四边形OACB的形状,并说明理由。试一试你的能力达标练习:
1、如图,在⊙O中,弧AB=弧AC,
∠B=70°. 则∠C= .2、如图,AB是直径,弧BC=弧CD=弧DE,∠BOC=40°,则∠AOE= 。5、圆不仅是轴对称图形,它也
是 图形.它与其他中
心对称图形的区别是 。6、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB6、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB6、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB 2、本节课我们通过实验得到了圆不仅是中心对称图形,而且还是轴对称图形,而由圆的对称性又得出许多圆的性质,即
在同一个圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。小结:本节课你有什么收获?1、圆心角 弦心距的概念结束寄语读书要从薄到厚,再从厚到薄.再见
由条件:
①∠AOB=∠A′O′B′③AB=A′B′在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。弦心距的概念弦心距 过圆心作弦的垂线,圆心与垂足之间的距离(如线段OC).想一想,在⊙O中,若圆心角∠AOB和∠A′OB′相等,则对应的弦心距OD与OD′相等吗?由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=OD′在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.讨论:1、在同圆或等圆中,如果弧相等,那么所对的圆心
角、所对的弦、所对弦的弦心距是否相等呢?2、在同圆或等圆中,如果弦相等,那么所对的圆心
角、所对的弧、所对弦的弦心距是否相等呢?如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等. 抢答题
已知:如图,AB,CD是⊙O的两条弦,
OE,OF为AB、CD的弦心距,根据这
节课所学的定理及推论填空:ABCFDEO(2)如果OE=OF,那么 , , ;(4)如果AB=CD,那么 , , 。(1)如果∠AOB=∠COD,那么 , , ;∠AOB=∠COD AB=CD OE=OF试一试你的能力 3、如图,在⊙O中,弧AC=弧BD,
求∠2的度数。4、下面的说法正确吗?为什么?如图,因为
根据圆心角、弧、弦、弦心距的关系定理
可知: 试一试你的能力抢答题试一试你的能力5.判断下列说法是否正确:
相等的圆心角所对的弧相等。( )
6.如图,⊙O中,AB=CD,
,则×7、在⊙O中,a、b为弦,他们
的弦心距分别为 c、d,若a>b,则( )
A c<d B c>d
C c=d D 无法确定8、已知A、B是⊙O上的两点∠AOB=120°, C是弧AB的中点,试确定四边形OACB的形状,并说明理由。试一试你的能力达标练习:
1、如图,在⊙O中,弧AB=弧AC,
∠B=70°. 则∠C= .2、如图,AB是直径,弧BC=弧CD=弧DE,∠BOC=40°,则∠AOE= 。5、圆不仅是轴对称图形,它也
是 图形.它与其他中
心对称图形的区别是 。6、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB6、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB6、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DB 2、本节课我们通过实验得到了圆不仅是中心对称图形,而且还是轴对称图形,而由圆的对称性又得出许多圆的性质,即
在同一个圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。小结:本节课你有什么收获?1、圆心角 弦心距的概念结束寄语读书要从薄到厚,再从厚到薄.再见
