浙江省嘉兴市海盐县2022-2023学年高一下学期期中考试数学试题(Word版含答案)
文档属性
| 名称 | 浙江省嘉兴市海盐县2022-2023学年高一下学期期中考试数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 577.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-21 15:32:49 | ||
图片预览



文档简介
海盐县2022-2023学年高一下学期期中考试
数学试卷
考试时间:120分钟
一、单选题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合要求的。
1.下列几何体中是旋转体的是( )
①圆柱;②六棱锥;③正方体;④球体;⑤四面体.
A.①和⑤ B.① C.③和④ D.①和④
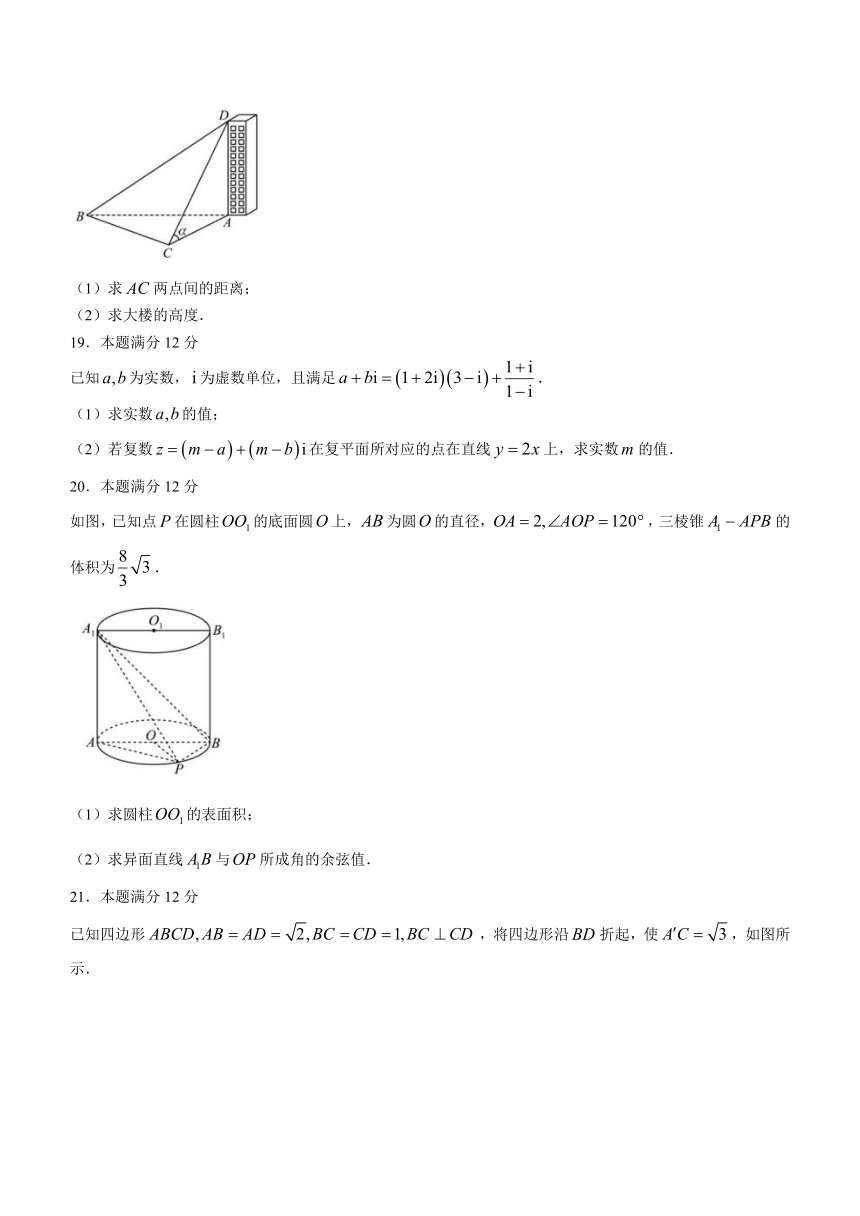
2.已知复数,(为虚数单位),若是纯虚数,则实数( )
A. B. C. D.3
3.已知平面和直线,则内至少有一条直线与( )
A.平行 B.相交 C.垂直 D.异面
4.向量,若,则( )
A. B. C. D.2
5.一个水平放置的平面图形的斜二测直观图是一个底角为,腰和上底边均为1的等腰梯形,则这个平面图形的面积是( )
A. B. C. D.
6.某款厨房用具中的香料收纳罐的实物图如图1所示,该几何体为上、下底面周长分别为,的正四棱台,若棱台的高为,忽略收纳罐的厚度,则该香料收纳罐的容积为( )
图1 图2
A. B. C. D.
7.某大学校园内有一个“少年湖”,湖的两侧有一个健身房和一个图书馆,如图,若设健身房在处,图书馆在处,为测量两地之间的距离,甲同学选定了与不共线的处,构成,以下是测量的数据的不同方案:①测量;②测量;③测量;④测量其中要求能唯一确定两地之间距离,甲同学应选择的方案的序号为( )
A.①② B.②③ C.②④ D.②③④
8.将3个半径为1的球和一个半径为的球叠为两层放在桌面上,上层只放一个较小的球,四个球两两相切,那么上层小球的最高点到桌面的距离是( )
A. B. C. D.
二、多选题:本大题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项是符合要求的。
9.如图,点是线段的三等分点,则下列结论正确的有( )
A. B. C. D.
10.如图,在四棱锥中,分别为上的点,且平面,则( )
A. B.平面 C. D.
11.已知向量不共线,若,且三点共线,则关于实数的值可以是( )
A. B. C. D.
12.如图,设分别是长方体的棱上的两个动点,点在点的左边,且满足,有下列结论:( )
A.平面 B.三棱锥体积为定值
C.平面 D.平面平面
三、填空题:本大题共4小题,每小题5分,共20分。
13.若复数(为虚数单位,),满足,则的值为_________.
14.已知向量,且在上的投影数量等于,则_________.
15.一个圆锥的表面积为,它的侧面展开图是圆心角为的扇形,则该圆锥的高为_________.
16.如图,正方形的边长都是1,而且平面互相垂直,点在上移动,点在上移动,若,则的长的最小值为_________.
三、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.本题满分10分
已知平面向量,且与的夹角为.
(1)求
(2)若与垂直,求k的值.
18.本题满分12分
某校学生利用解三角形有关知识进行数学实践活动.A处有一栋大楼,某学生选两处作为测量点,测得的距离为,在处测得大楼楼顶的仰角为.
(1)求两点间的距离;
(2)求大楼的高度.
19.本题满分12分
已知为实数,为虚数单位,且满足.
(1)求实数的值;
(2)若复数在复平面所对应的点在直线上,求实数的值.
20.本题满分12分
如图,已知点在圆柱的底面圆上,为圆的直径,,三棱锥的体积为.
(1)求圆柱的表面积;
(2)求异面直线与所成角的余弦值.
21.本题满分12分
已知四边形,将四边形沿折起,使,如图所示.
(1)求证:;
(2)求二面角的余弦值.
22.本题满分12分
在中,角的对边分别是,且.
(1)求角的大小;
(2)若为边上的一点,,且_________,求的面积.
请在下列两个条件中选择一个作为条件补充在横线上,并解决问题.
(1)是的平分线;(2)D为线段的中点.
海盐县2022-2023学年高一下学期期中考试
答案
一、二 选择题答案:
1 2 3 4 5 6 7 8 9 10 11 12
D A C C B C C A ACD BD CD BD
三、填空题:
14. 0或-2 15. 16.
解答题
17【答案】(1)
(2)
18、【详解】(1)因为,
在中,由正弦定理得,
即,所以m,
即AC两点的距离为m;
(2)在中,因为,,
所以,
又,
所以m,
即大楼的高度为m.
19、【答案】(1),;(2).
【分析】(1)利用复数的相等的概念以及复数的四则运算进行求解.
(2)利用复数的几何意义求解.
【详解】(1)因为,
所以.
(2)由(1)有:,
因为在复平面所对应的点是,且在直线上,所以.
解得.
20、(1)是圆O的直径,.
由题意,在中,,
,即,
在中,,,
又三棱锥的体积为,
由,解得,
故圆柱的表面积为:.
(2)取中点,连接,,
则,且.
或它的补角为异面直线与所成的角,
又, ,
在中,由余弦定理得,,
异面直线与所成角余弦值为.
21.(1)取的中点,连,
,
平面
(2)
是正三角形,,
,
即
取的中点,连,
则,且
因为,所以即二面角的平面角
22、【答案】(1)
(2)
【分析】(1)利用正弦定理边化角,结合两角和的正弦公式即可求解;
(2)选择①,由平分得,分别用三角形面积公式求解可得,利用余弦定理可得,联立即可求解的值,即可求得△ABC的面积;选择②,利用平面向量的线性运算可得,求解向量的模可得,利用余弦定理可得,联立即可求解的值,即可求得△ABC的面积.
【详解】(1)解:由正弦定理知,,
∵,
代入上式得,
∵,
∴,,
∵,∴.
(2)若选①:
由平分得,,
∴,
即.
在中,由余弦定理得,
又,∴,
联立得,
解得,(舍去),
∴.
若选②:
因为,,
,得,
在中,由余弦定理得,
即,
联立,可得,
∴.
数学试卷
考试时间:120分钟
一、单选题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合要求的。
1.下列几何体中是旋转体的是( )
①圆柱;②六棱锥;③正方体;④球体;⑤四面体.
A.①和⑤ B.① C.③和④ D.①和④
2.已知复数,(为虚数单位),若是纯虚数,则实数( )
A. B. C. D.3
3.已知平面和直线,则内至少有一条直线与( )
A.平行 B.相交 C.垂直 D.异面
4.向量,若,则( )
A. B. C. D.2
5.一个水平放置的平面图形的斜二测直观图是一个底角为,腰和上底边均为1的等腰梯形,则这个平面图形的面积是( )
A. B. C. D.
6.某款厨房用具中的香料收纳罐的实物图如图1所示,该几何体为上、下底面周长分别为,的正四棱台,若棱台的高为,忽略收纳罐的厚度,则该香料收纳罐的容积为( )
图1 图2
A. B. C. D.
7.某大学校园内有一个“少年湖”,湖的两侧有一个健身房和一个图书馆,如图,若设健身房在处,图书馆在处,为测量两地之间的距离,甲同学选定了与不共线的处,构成,以下是测量的数据的不同方案:①测量;②测量;③测量;④测量其中要求能唯一确定两地之间距离,甲同学应选择的方案的序号为( )
A.①② B.②③ C.②④ D.②③④
8.将3个半径为1的球和一个半径为的球叠为两层放在桌面上,上层只放一个较小的球,四个球两两相切,那么上层小球的最高点到桌面的距离是( )
A. B. C. D.
二、多选题:本大题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项是符合要求的。
9.如图,点是线段的三等分点,则下列结论正确的有( )
A. B. C. D.
10.如图,在四棱锥中,分别为上的点,且平面,则( )
A. B.平面 C. D.
11.已知向量不共线,若,且三点共线,则关于实数的值可以是( )
A. B. C. D.
12.如图,设分别是长方体的棱上的两个动点,点在点的左边,且满足,有下列结论:( )
A.平面 B.三棱锥体积为定值
C.平面 D.平面平面
三、填空题:本大题共4小题,每小题5分,共20分。
13.若复数(为虚数单位,),满足,则的值为_________.
14.已知向量,且在上的投影数量等于,则_________.
15.一个圆锥的表面积为,它的侧面展开图是圆心角为的扇形,则该圆锥的高为_________.
16.如图,正方形的边长都是1,而且平面互相垂直,点在上移动,点在上移动,若,则的长的最小值为_________.
三、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.本题满分10分
已知平面向量,且与的夹角为.
(1)求
(2)若与垂直,求k的值.
18.本题满分12分
某校学生利用解三角形有关知识进行数学实践活动.A处有一栋大楼,某学生选两处作为测量点,测得的距离为,在处测得大楼楼顶的仰角为.
(1)求两点间的距离;
(2)求大楼的高度.
19.本题满分12分
已知为实数,为虚数单位,且满足.
(1)求实数的值;
(2)若复数在复平面所对应的点在直线上,求实数的值.
20.本题满分12分
如图,已知点在圆柱的底面圆上,为圆的直径,,三棱锥的体积为.
(1)求圆柱的表面积;
(2)求异面直线与所成角的余弦值.
21.本题满分12分
已知四边形,将四边形沿折起,使,如图所示.
(1)求证:;
(2)求二面角的余弦值.
22.本题满分12分
在中,角的对边分别是,且.
(1)求角的大小;
(2)若为边上的一点,,且_________,求的面积.
请在下列两个条件中选择一个作为条件补充在横线上,并解决问题.
(1)是的平分线;(2)D为线段的中点.
海盐县2022-2023学年高一下学期期中考试
答案
一、二 选择题答案:
1 2 3 4 5 6 7 8 9 10 11 12
D A C C B C C A ACD BD CD BD
三、填空题:
14. 0或-2 15. 16.
解答题
17【答案】(1)
(2)
18、【详解】(1)因为,
在中,由正弦定理得,
即,所以m,
即AC两点的距离为m;
(2)在中,因为,,
所以,
又,
所以m,
即大楼的高度为m.
19、【答案】(1),;(2).
【分析】(1)利用复数的相等的概念以及复数的四则运算进行求解.
(2)利用复数的几何意义求解.
【详解】(1)因为,
所以.
(2)由(1)有:,
因为在复平面所对应的点是,且在直线上,所以.
解得.
20、(1)是圆O的直径,.
由题意,在中,,
,即,
在中,,,
又三棱锥的体积为,
由,解得,
故圆柱的表面积为:.
(2)取中点,连接,,
则,且.
或它的补角为异面直线与所成的角,
又, ,
在中,由余弦定理得,,
异面直线与所成角余弦值为.
21.(1)取的中点,连,
,
平面
(2)
是正三角形,,
,
即
取的中点,连,
则,且
因为,所以即二面角的平面角
22、【答案】(1)
(2)
【分析】(1)利用正弦定理边化角,结合两角和的正弦公式即可求解;
(2)选择①,由平分得,分别用三角形面积公式求解可得,利用余弦定理可得,联立即可求解的值,即可求得△ABC的面积;选择②,利用平面向量的线性运算可得,求解向量的模可得,利用余弦定理可得,联立即可求解的值,即可求得△ABC的面积.
【详解】(1)解:由正弦定理知,,
∵,
代入上式得,
∵,
∴,,
∵,∴.
(2)若选①:
由平分得,,
∴,
即.
在中,由余弦定理得,
又,∴,
联立得,
解得,(舍去),
∴.
若选②:
因为,,
,得,
在中,由余弦定理得,
即,
联立,可得,
∴.
同课章节目录
