2023-2024学年吉林省长春市博硕学校高三(上)期初数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年吉林省长春市博硕学校高三(上)期初数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 318.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-21 15:35:13 | ||
图片预览




文档简介
2023-2024学年吉林省长春市博硕学校高三(上)期初数学试卷
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知集合,下列选项正确的是( )
A. B. C. D.
2. 是的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
3. 某市一次高三模拟考试一共有万名考生参加,他们的总分服从正态分布,若,则总分高于分的考生人数为( )
A. B. C. D.
4. 已知,则等于( )
A. B. C. D.
5. 在射击比赛中,甲乙两人对同一目标各进行一次射击,甲击中目标的概率为,乙击中目标的概率为,在目标被击中的情况下,甲击中目标的概率为( )
A. B. C. D.
6. 设某医院仓库中有盒同样规格的光片,已知其中有盒、盒、盒依次是甲厂、乙厂、丙厂生产的.且甲、乙、丙三厂生产该种光片的次品率依次为,,,现从这盒中任取一盒,再从这盒中任取一张光片,则取得的光片是次品的概率为( )
A. B. C. D.
7. 为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑期开设“礼”“乐”“射”“御”“书”“数”六门体验课程,每周一门,连续开设六周若课程“乐”不排在第一周,课程“御”不排在最后一周,则所有可能的排法种数为( )
A. B. C. D.
8. 已知函数满足对任意恒成立,且时,则的值为( )
A. B. C. D.
二、多选题(本大题共2小题,共10.0分。在每小题有多项符合题目要求)
9. 下列命题为真命题的是( )
A. 若,则
B. 若,则
C. 若关于的不等式的解集为,则
D. 若,,则“”是“”的必要不充分条件
10. 已知函数,则( )
A. 在是增函数
B. 有极大值点,且
C. 的极小值点,且
D. 没有零点
三、填空题(本大题共4小题,共20.0分)
11. 函数的定义域是______.
12. 曲线在点处的切线方程为______.
13. 已知,是正实数,函数的图像经过点,则的最小值为______ .
14. 已知定义在上的连续函数满足:
在上单调;
;
对恒成立;
对恒成立.
若,,,,记与形成的封闭图形的面积为,,则满足的最小的的值为______ .
四、解答题(本大题共4小题,共50.0分。解答应写出文字说明,证明过程或演算步骤)
15. 本小题分
已知.
解上述不等式;
在的条件下,求函数的最大值和最小值及对应的的值.
16. 本小题分
甲乙两所友好学校举行篮球联谊赛,先获得场比赛胜利的学校获得冠军并终止比赛,比赛交替在甲校与乙校进行,第一场比赛在甲校进行已知甲队在主场甲校获胜的概率为,在客场乙校获胜的概率为,每场比赛要分出胜负且胜负概率不变.
求甲队以胜负的成绩赢得冠军的概率;
设篮球联谊赛比赛进行的场数为,求随机变量的分布列与期望.
17. 本小题分
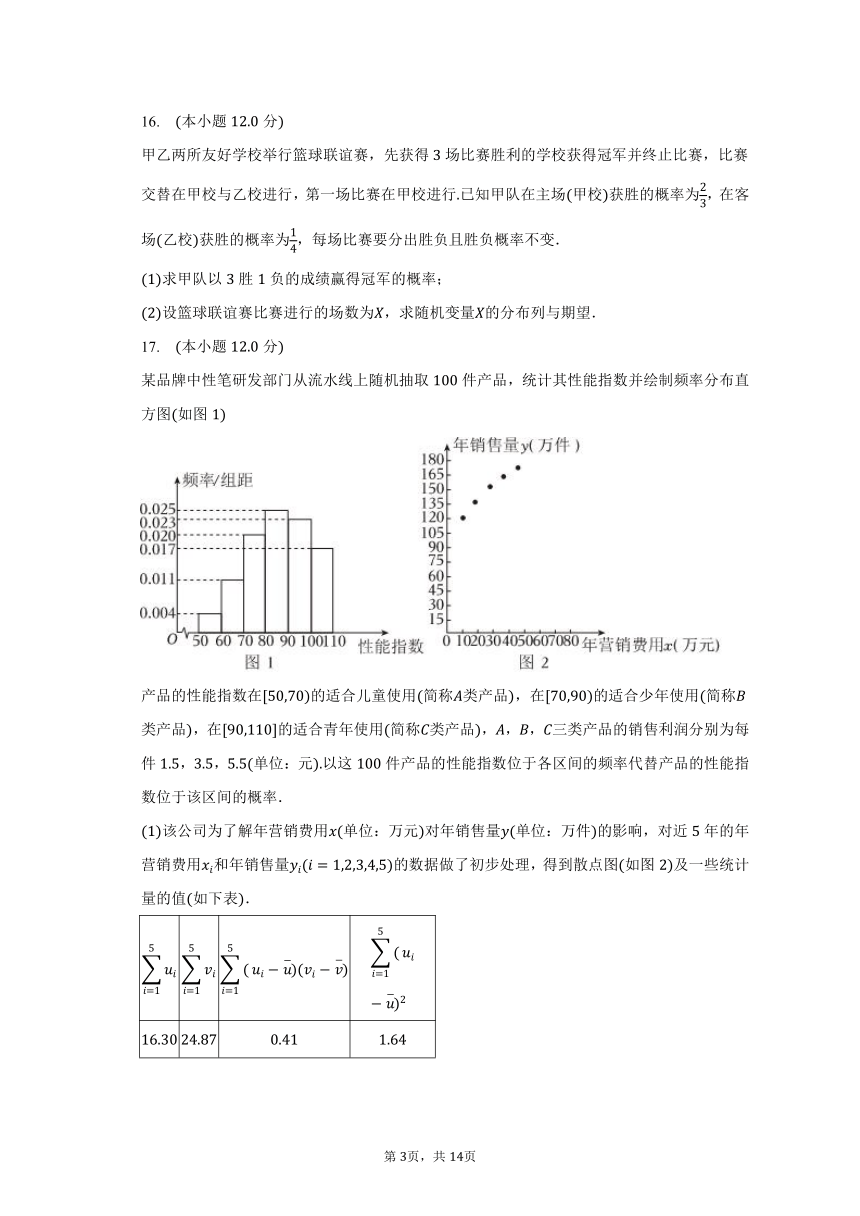
某品牌中性笔研发部门从流水线上随机抽取件产品,统计其性能指数并绘制频率分布直方图如图
产品的性能指数在的适合儿童使用简称类产品,在的适合少年使用简称类产品,在的适合青年使用简称类产品,,,三类产品的销售利润分别为每件,,单位:元以这件产品的性能指数位于各区间的频率代替产品的性能指数位于该区间的概率.
该公司为了解年营销费用单位:万元对年销售量单位:万件的影响,对近年的年营销费用和年销售量的数据做了初步处理,得到散点图如图及一些统计量的值如下表.
表中.
根据散点图判断,可以作为年销售量万件关于年营销费用万元的回归方程,求关于的回归方程;取
求每件产品的平均销售利润;并用所求的回归方程估计该公司应投入多少营销费,才能使得该产品一年的收益达到最大?收益销售利润营销费用
参考公式:对于一组数据,,,,其回归直线的斜率和截距的最小二乘估计分别为.
18. 本小题分
证明:当时,;
是否存在正数,使得在上单调递增,若存在,求出的取值范围;若不存在,请说明理由.
答案和解析
1.【答案】
【解析】解:因为集合,
则是集合的子集,所以C错误,D正确,
因为集合间是包含关系,所以,B错误,
故选:.
根据集合的元素以及集合间的包含关系的定义对应各个选项即可判断求解.
本题考查了集合的包含关系的应用,考查了学生的分析问题的能力,属于基础题.
2.【答案】
【解析】解:,,
,或,
,
是的充分不必要条件,
故选:.
先解指数不等式,一元二次不等式,再利用充要条件的定义判定即可.
本题考查了指数不等式,一元二次不等式的解法,充要条件的判定,属于中档题.
3.【答案】
【解析】解:总分服从正态分布,,
,
,
总分高于分的考生人数为.
故选:.
根据已知条件,结合正态分布的对称性,考查频率与频数的关系,即可求解.
本题主要考查正态分布的对称性,考查频率与频数的关系,属于基础题.
4.【答案】
【解析】解:由二项式定理得,
即,所以,所以,
故选:.
逆用二项式定理建立方程求出的值,进而可以求解.
本题考查了二项式定理的应用,考查了学生的运算求解能力,属于基础题.
5.【答案】
【解析】解:由题意得目标被击中的概率为:,
甲击中目标的概率为:,
则在目标被击中的情况下,甲击中目标的概率为:.
故选:.
先得出目标被击中的概率,再得出甲击中目标的概率,即可得出答案.
本题主要考查条件概率公式,属于基础题.
6.【答案】
【解析】【分析】
本题考查概率的求法,考查全概率公式等基础知识,考查运算求解能力,是中档题.
以,,分别表示取得的这盒光片是由甲厂、乙厂、丙厂生产的,表示取得的光片为次品,由全概率公式能求出结果.
【解答】
解:以,,分别表示取得的这盒光片是由甲厂、乙厂、丙厂生产的,表示取得的光片为次品,
,,,
,,,
由全概率公式得:
.
故选:.
7.【答案】
【解析】解:根据题意,分种情况讨论:
,“御”排在第一,将剩下的“五艺”全排列,安排在剩下的周,有种排法,
,“御”不排在第一,则“御”的排法有种,“乐”的排法有种,将剩下的“四艺”全排列,安排在剩下的周,有种情况,
则此时有种排法,
则一共有种排法;
故选:.
根据题意,分种情况讨论:,“御”排在第一,将剩下的“五艺”全排列,安排在剩下的周;,“御”不排在第一,由分步计数原理求出此时的排法数目,进而由加法原理计算可得答案.
本题考查排列、组合的应用,涉及分步、分类计数原理的应用,属于基础题.
8.【答案】
【解析】解:根据题意,函数满足对任意恒成立,
,
用替换,则,,
函数是以为周期的周期函数,
,,
,
,
则.
故选:.
由条件可得函数是以为周期的周期函数,再由指对数的运算法则和函数的周期性计算即可.
本题考查抽象函数的周期性,指对数的运算,属于中档题.
9.【答案】
【解析】解:对于:当,时,不等式的关系不成立,故A错误;
对于:由于,所以,故,故B正确;
对于:若关于的不等式的解集为,所以和相当于的两根,所以,整理得,,整理得,故,故C正确;
对于:若,,则“”整理得,故,反之不成立,故“”是“”的充分不必要条件,故D错误.
故选:.
直接利用不等式的性质,基本不等式的应用,充分条件和必要条件的应用,判断、、、的结论.
本题考查的知识要点:不等式的性质,基本不等式的应用,充分条件和必要条件的应用,主要考查学生的运算能力和数学思维能力,属于中档题.
10.【答案】
【解析】解:已知,函数定义域为,
可得,
当时,,
所以,
即,单调递增,故选项A正确;
令,
解得,
当时,,单调递减;
当时,,单调递增,
因为,
所以,
而函数的极小值点为,故选项B错误,选项C正确;
因为,
所以函数没有零点,故选项D正确.
故选:.
由题意,对函数进行求导,利用导数得到函数的单调性和极值,再对选项进行逐一分析即可.
本题考查利用导数研究函数的单调性,考查了逻辑推理能力.
11.【答案】或
【解析】解:由题意得,
解答或.
故答案为:或.
根据函数的解析式,列出使函数解析式有意义的不等式组,求出解集即可
本题考查了求函数定义域的应用问题,解题的关键是列出使函数解析式有意义的不等式组,是基础题目
12.【答案】
【解析】解:由题意可得:,
所以在点处的切线斜率为,
所以在点处的切线方程为:.
故答案为:.
由题意求出导数:,进而根据切点坐标求出切线的斜率,即可求出切线的方程.
此题考查学生熟练利用导数求曲线上过某点切线方程的斜率,能够根据一点坐标和斜率写出直线的方程,是一道基础题.
13.【答案】
【解析】解:由题意有:,即,
则
,
当且仅当,即,时等号成立.
故答案为:.
由函数经过定点,得到,再利用整体代换思想代入所求式,运用基本不等式求最小值即可.
本题考查运用基本不等式求最值的运用,属基础题.
14.【答案】
【解析】解:由题意可知当,的函数图像关于对称,
当,的函数图像关于直线对称,
其图像如下:
根据对称性可知与所围几何图形面积为,即,
由于,,所以,
即,以此类推,有,,
即数列是以为首项,为公比的等比数列,
所以,
由于,,且数列为正项数列,
所以所求的最小值为.
故答案为:.
由题意可知当,的函数图像关于对称,当,的函数图像关于直线对称,根据对称性可求出,由于,,所以
,即,以此类推,,由此即可求出不等式的解.
本题主要考查抽象函数性质以及等比数列性质,属中档题.
15.【答案】解:由,可得,求得,
所以,不等式的解集为.
对于函数,
令,由于,可得,
则.
当时,即时,;当时,即时,.
【解析】由题意利用对数函数的定义域和单调性,解对数不等式,求得的范围.
由题意利用指数函数的定义域和值域,可得 的范围,再利用二次函数的性质,求得函数的最大值和最小值及对应的的值.
本题主要考查对数不等式的解法,指数函数的定义域和值域,二次函数的性质,属于中档题.
16.【答案】解:设事件为:“甲队以胜负的成绩赢得冠军”,
则;
由题意:的可能取值为,,.
则,
,
,
故随机变量的分布列为:
.
【解析】利用概率公式可求甲队以胜负的成绩赢得冠军的概率;
的可能取值为,,计算可求随机变量的分布列与期望.
本题考查求随机变量的分布列与期望,考查运算求解能力,属中档题.
17.【答案】解:由,得,
令,,,则,
则,
则,
,
即,
,,
所求的回归方程为;
设每件产品的销售利润为元,则的所有可能取值为,,,
由直方图可得,,,三类产品的频率分别为,,,
,
,
.
随机变量的分布列为:
则,
故每件产品的平均销售利润为元;
设年收益为万元,则,
设,则,
当时,,在单週递增,
当时,,在单调递减,
当,即时,有最大值为.
估计当该公司一年投入万元营销费时,能使得该产品年收益达到最大.
【解析】根据表中数据求出相应参数,即可得到回归方程;
求出每件产品的销售利润的分布列,得出均值,即每件产品的平均销售利润,求出年收益的表达式,通过求导得出该公司在该产品一年的收益达到最大时应投入的营销费.
本题考查回归方程的求法,考查化归与转化思想,训练了利用导数求最值,是中档题.
18.【答案】解:证明:不妨设,函数定义域为,
可得,
当时,,单调递减;
当时,,单调递增,
所以,
则,
所以,
当时,整理得,
则当时,;
已知,函数定义域为,
可得,
不妨设,函数定义域为,
可得,
若在上单调递增,
则在上恒成立,
又,
此时在处取得最小值,
要使其符合题意,此时,
解得,
当时,,
可得,
可得,
不妨设,函数定义域为,
可得,单调递增,
所以,
不妨设,函数定义域为,
可得,单调递减,
所以,
若,
此时,
所以在上单调递增,
即在上单调递增;
若,
当时,可得
,
当时,可得,
所以函数在上单调递减,
即在上单调递减,
则,
所以当时,函数在上单调递增,
当时,
由知,
,
当时,,单调递减,不符合题意;
当时,
同理得当时,,
当时,,单调递减,不符合题意,
综上,当时,在上单调递增.
【解析】由题意,设,对进行求导,利用导数得到函数的单调性和最值,此时,易得,故不等式成立;
对函数进行求导,构造函数,对函数进行求导,由在上单调递增,得到在上恒成立,要使条件成立,需满足在处取得最小值,求出的值后再对进行检验即可求解.
本题考查利用导数研究函数的单调性以及不等式恒成立问题,考查了逻辑推理、分类讨论、转化思想和运算能力.
第1页,共1页
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知集合,下列选项正确的是( )
A. B. C. D.
2. 是的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
3. 某市一次高三模拟考试一共有万名考生参加,他们的总分服从正态分布,若,则总分高于分的考生人数为( )
A. B. C. D.
4. 已知,则等于( )
A. B. C. D.
5. 在射击比赛中,甲乙两人对同一目标各进行一次射击,甲击中目标的概率为,乙击中目标的概率为,在目标被击中的情况下,甲击中目标的概率为( )
A. B. C. D.
6. 设某医院仓库中有盒同样规格的光片,已知其中有盒、盒、盒依次是甲厂、乙厂、丙厂生产的.且甲、乙、丙三厂生产该种光片的次品率依次为,,,现从这盒中任取一盒,再从这盒中任取一张光片,则取得的光片是次品的概率为( )
A. B. C. D.
7. 为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑期开设“礼”“乐”“射”“御”“书”“数”六门体验课程,每周一门,连续开设六周若课程“乐”不排在第一周,课程“御”不排在最后一周,则所有可能的排法种数为( )
A. B. C. D.
8. 已知函数满足对任意恒成立,且时,则的值为( )
A. B. C. D.
二、多选题(本大题共2小题,共10.0分。在每小题有多项符合题目要求)
9. 下列命题为真命题的是( )
A. 若,则
B. 若,则
C. 若关于的不等式的解集为,则
D. 若,,则“”是“”的必要不充分条件
10. 已知函数,则( )
A. 在是增函数
B. 有极大值点,且
C. 的极小值点,且
D. 没有零点
三、填空题(本大题共4小题,共20.0分)
11. 函数的定义域是______.
12. 曲线在点处的切线方程为______.
13. 已知,是正实数,函数的图像经过点,则的最小值为______ .
14. 已知定义在上的连续函数满足:
在上单调;
;
对恒成立;
对恒成立.
若,,,,记与形成的封闭图形的面积为,,则满足的最小的的值为______ .
四、解答题(本大题共4小题,共50.0分。解答应写出文字说明,证明过程或演算步骤)
15. 本小题分
已知.
解上述不等式;
在的条件下,求函数的最大值和最小值及对应的的值.
16. 本小题分
甲乙两所友好学校举行篮球联谊赛,先获得场比赛胜利的学校获得冠军并终止比赛,比赛交替在甲校与乙校进行,第一场比赛在甲校进行已知甲队在主场甲校获胜的概率为,在客场乙校获胜的概率为,每场比赛要分出胜负且胜负概率不变.
求甲队以胜负的成绩赢得冠军的概率;
设篮球联谊赛比赛进行的场数为,求随机变量的分布列与期望.
17. 本小题分
某品牌中性笔研发部门从流水线上随机抽取件产品,统计其性能指数并绘制频率分布直方图如图
产品的性能指数在的适合儿童使用简称类产品,在的适合少年使用简称类产品,在的适合青年使用简称类产品,,,三类产品的销售利润分别为每件,,单位:元以这件产品的性能指数位于各区间的频率代替产品的性能指数位于该区间的概率.
该公司为了解年营销费用单位:万元对年销售量单位:万件的影响,对近年的年营销费用和年销售量的数据做了初步处理,得到散点图如图及一些统计量的值如下表.
表中.
根据散点图判断,可以作为年销售量万件关于年营销费用万元的回归方程,求关于的回归方程;取
求每件产品的平均销售利润;并用所求的回归方程估计该公司应投入多少营销费,才能使得该产品一年的收益达到最大?收益销售利润营销费用
参考公式:对于一组数据,,,,其回归直线的斜率和截距的最小二乘估计分别为.
18. 本小题分
证明:当时,;
是否存在正数,使得在上单调递增,若存在,求出的取值范围;若不存在,请说明理由.
答案和解析
1.【答案】
【解析】解:因为集合,
则是集合的子集,所以C错误,D正确,
因为集合间是包含关系,所以,B错误,
故选:.
根据集合的元素以及集合间的包含关系的定义对应各个选项即可判断求解.
本题考查了集合的包含关系的应用,考查了学生的分析问题的能力,属于基础题.
2.【答案】
【解析】解:,,
,或,
,
是的充分不必要条件,
故选:.
先解指数不等式,一元二次不等式,再利用充要条件的定义判定即可.
本题考查了指数不等式,一元二次不等式的解法,充要条件的判定,属于中档题.
3.【答案】
【解析】解:总分服从正态分布,,
,
,
总分高于分的考生人数为.
故选:.
根据已知条件,结合正态分布的对称性,考查频率与频数的关系,即可求解.
本题主要考查正态分布的对称性,考查频率与频数的关系,属于基础题.
4.【答案】
【解析】解:由二项式定理得,
即,所以,所以,
故选:.
逆用二项式定理建立方程求出的值,进而可以求解.
本题考查了二项式定理的应用,考查了学生的运算求解能力,属于基础题.
5.【答案】
【解析】解:由题意得目标被击中的概率为:,
甲击中目标的概率为:,
则在目标被击中的情况下,甲击中目标的概率为:.
故选:.
先得出目标被击中的概率,再得出甲击中目标的概率,即可得出答案.
本题主要考查条件概率公式,属于基础题.
6.【答案】
【解析】【分析】
本题考查概率的求法,考查全概率公式等基础知识,考查运算求解能力,是中档题.
以,,分别表示取得的这盒光片是由甲厂、乙厂、丙厂生产的,表示取得的光片为次品,由全概率公式能求出结果.
【解答】
解:以,,分别表示取得的这盒光片是由甲厂、乙厂、丙厂生产的,表示取得的光片为次品,
,,,
,,,
由全概率公式得:
.
故选:.
7.【答案】
【解析】解:根据题意,分种情况讨论:
,“御”排在第一,将剩下的“五艺”全排列,安排在剩下的周,有种排法,
,“御”不排在第一,则“御”的排法有种,“乐”的排法有种,将剩下的“四艺”全排列,安排在剩下的周,有种情况,
则此时有种排法,
则一共有种排法;
故选:.
根据题意,分种情况讨论:,“御”排在第一,将剩下的“五艺”全排列,安排在剩下的周;,“御”不排在第一,由分步计数原理求出此时的排法数目,进而由加法原理计算可得答案.
本题考查排列、组合的应用,涉及分步、分类计数原理的应用,属于基础题.
8.【答案】
【解析】解:根据题意,函数满足对任意恒成立,
,
用替换,则,,
函数是以为周期的周期函数,
,,
,
,
则.
故选:.
由条件可得函数是以为周期的周期函数,再由指对数的运算法则和函数的周期性计算即可.
本题考查抽象函数的周期性,指对数的运算,属于中档题.
9.【答案】
【解析】解:对于:当,时,不等式的关系不成立,故A错误;
对于:由于,所以,故,故B正确;
对于:若关于的不等式的解集为,所以和相当于的两根,所以,整理得,,整理得,故,故C正确;
对于:若,,则“”整理得,故,反之不成立,故“”是“”的充分不必要条件,故D错误.
故选:.
直接利用不等式的性质,基本不等式的应用,充分条件和必要条件的应用,判断、、、的结论.
本题考查的知识要点:不等式的性质,基本不等式的应用,充分条件和必要条件的应用,主要考查学生的运算能力和数学思维能力,属于中档题.
10.【答案】
【解析】解:已知,函数定义域为,
可得,
当时,,
所以,
即,单调递增,故选项A正确;
令,
解得,
当时,,单调递减;
当时,,单调递增,
因为,
所以,
而函数的极小值点为,故选项B错误,选项C正确;
因为,
所以函数没有零点,故选项D正确.
故选:.
由题意,对函数进行求导,利用导数得到函数的单调性和极值,再对选项进行逐一分析即可.
本题考查利用导数研究函数的单调性,考查了逻辑推理能力.
11.【答案】或
【解析】解:由题意得,
解答或.
故答案为:或.
根据函数的解析式,列出使函数解析式有意义的不等式组,求出解集即可
本题考查了求函数定义域的应用问题,解题的关键是列出使函数解析式有意义的不等式组,是基础题目
12.【答案】
【解析】解:由题意可得:,
所以在点处的切线斜率为,
所以在点处的切线方程为:.
故答案为:.
由题意求出导数:,进而根据切点坐标求出切线的斜率,即可求出切线的方程.
此题考查学生熟练利用导数求曲线上过某点切线方程的斜率,能够根据一点坐标和斜率写出直线的方程,是一道基础题.
13.【答案】
【解析】解:由题意有:,即,
则
,
当且仅当,即,时等号成立.
故答案为:.
由函数经过定点,得到,再利用整体代换思想代入所求式,运用基本不等式求最小值即可.
本题考查运用基本不等式求最值的运用,属基础题.
14.【答案】
【解析】解:由题意可知当,的函数图像关于对称,
当,的函数图像关于直线对称,
其图像如下:
根据对称性可知与所围几何图形面积为,即,
由于,,所以,
即,以此类推,有,,
即数列是以为首项,为公比的等比数列,
所以,
由于,,且数列为正项数列,
所以所求的最小值为.
故答案为:.
由题意可知当,的函数图像关于对称,当,的函数图像关于直线对称,根据对称性可求出,由于,,所以
,即,以此类推,,由此即可求出不等式的解.
本题主要考查抽象函数性质以及等比数列性质,属中档题.
15.【答案】解:由,可得,求得,
所以,不等式的解集为.
对于函数,
令,由于,可得,
则.
当时,即时,;当时,即时,.
【解析】由题意利用对数函数的定义域和单调性,解对数不等式,求得的范围.
由题意利用指数函数的定义域和值域,可得 的范围,再利用二次函数的性质,求得函数的最大值和最小值及对应的的值.
本题主要考查对数不等式的解法,指数函数的定义域和值域,二次函数的性质,属于中档题.
16.【答案】解:设事件为:“甲队以胜负的成绩赢得冠军”,
则;
由题意:的可能取值为,,.
则,
,
,
故随机变量的分布列为:
.
【解析】利用概率公式可求甲队以胜负的成绩赢得冠军的概率;
的可能取值为,,计算可求随机变量的分布列与期望.
本题考查求随机变量的分布列与期望,考查运算求解能力,属中档题.
17.【答案】解:由,得,
令,,,则,
则,
则,
,
即,
,,
所求的回归方程为;
设每件产品的销售利润为元,则的所有可能取值为,,,
由直方图可得,,,三类产品的频率分别为,,,
,
,
.
随机变量的分布列为:
则,
故每件产品的平均销售利润为元;
设年收益为万元,则,
设,则,
当时,,在单週递增,
当时,,在单调递减,
当,即时,有最大值为.
估计当该公司一年投入万元营销费时,能使得该产品年收益达到最大.
【解析】根据表中数据求出相应参数,即可得到回归方程;
求出每件产品的销售利润的分布列,得出均值,即每件产品的平均销售利润,求出年收益的表达式,通过求导得出该公司在该产品一年的收益达到最大时应投入的营销费.
本题考查回归方程的求法,考查化归与转化思想,训练了利用导数求最值,是中档题.
18.【答案】解:证明:不妨设,函数定义域为,
可得,
当时,,单调递减;
当时,,单调递增,
所以,
则,
所以,
当时,整理得,
则当时,;
已知,函数定义域为,
可得,
不妨设,函数定义域为,
可得,
若在上单调递增,
则在上恒成立,
又,
此时在处取得最小值,
要使其符合题意,此时,
解得,
当时,,
可得,
可得,
不妨设,函数定义域为,
可得,单调递增,
所以,
不妨设,函数定义域为,
可得,单调递减,
所以,
若,
此时,
所以在上单调递增,
即在上单调递增;
若,
当时,可得
,
当时,可得,
所以函数在上单调递减,
即在上单调递减,
则,
所以当时,函数在上单调递增,
当时,
由知,
,
当时,,单调递减,不符合题意;
当时,
同理得当时,,
当时,,单调递减,不符合题意,
综上,当时,在上单调递增.
【解析】由题意,设,对进行求导,利用导数得到函数的单调性和最值,此时,易得,故不等式成立;
对函数进行求导,构造函数,对函数进行求导,由在上单调递增,得到在上恒成立,要使条件成立,需满足在处取得最小值,求出的值后再对进行检验即可求解.
本题考查利用导数研究函数的单调性以及不等式恒成立问题,考查了逻辑推理、分类讨论、转化思想和运算能力.
第1页,共1页
同课章节目录
