1.2.4 绝对值的化简 培优练习(无答案) 2023--2024学年人教版七年级数学上册
文档属性
| 名称 | 1.2.4 绝对值的化简 培优练习(无答案) 2023--2024学年人教版七年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 153.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 15:32:54 | ||
图片预览


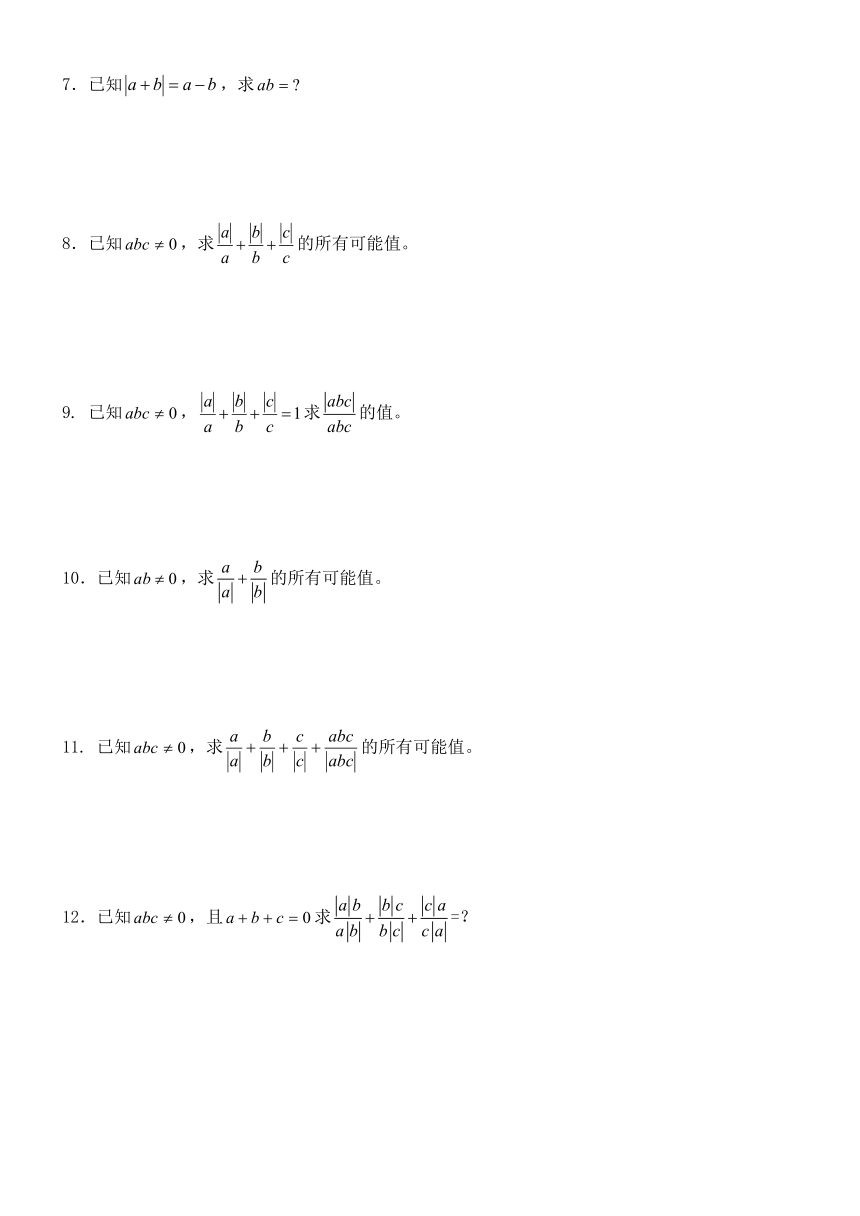


文档简介
【初一专题】绝对值的化简
【考点回顾】
(1)绝对值的几何意义:一个数a的绝对值就是数轴上表示数a的点与原点的距离,数a的绝对值记作|a|.
(2)绝对值的代数意义:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.
【注意】
①取绝对值也是一种运算,运算符号是“||”,求一个数的绝对值,就是根据性质去掉绝对值符号.
②绝对值的性质:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.
③绝对值具有非负性,取绝对值的结果总是正数或0.
④任何一个有理数都是由两部分组成:符号和它的绝对值,如-5符号是负号,绝对值是5.
(3)求字母a的绝对值:
① ② ③
(4)利用绝对值比较两个负有理数的大小:两个负数,绝对值大的反而小.
(5)绝对值非负性:如果若干个非负数的和为0,那么这若干个非负数都必为0.例如:若|a|+|b|+|c|=0,则a=0,b=0,c=0.
(6)其它重要性质:
①任何一个数的绝对值都不小于这个数,也不小于这个数的相反数,即|a|≥a,且|a|≥-a;
②若|a|=|b|,则a=b或a=-b;
③;;
④|a| =|a |=a ;
⑤||a|-|b||≤|a+b|≤|a|+|b|,对于|a+b|≤|a|+|b|,等号当且仅当a、b同号或a、b中至少有一个0时,等号成立;对于||a|-|b||≤|a+b|,等号当且仅当a、b异号或a、b中至少有一个0时,等号成立.
(7)绝对值的几何意义:当x=a时,|x-a|=0,此时a是|x-a|的零点值.
|a|的几何意义:在数轴上,表示这个数的点离开原点的距离.
|a-b|的几何意义:在数轴上,表示数a、b对应数轴上两点间的距离.
【分类强化】
(一)分类讨论
1.已知,求的所有可能值。
2.已知,求的所有可能值。
3.已知,且,求的所有可能值。
4.已知,且,求的所有可能值。
5.已知,且,求的所有可能值。
6.已知,且,求的所有可能值。
7.已知,求
8.已知,求的所有可能值。
9. 已知,求的值。
10.已知,求的所有可能值。
11. 已知,求的所有可能值。
12.已知,且求=?
(二)绝对值的非负性
已知,求的值。
2.已知,求的值。
3. 已知,求的值。
4.已知与互为相反数,求得值。
5.已知,求的值。
6.若,则=?
(三)比较大小
1.若,则用“<”把连接起来。
2.若,则用“<”把连接起来。
3. 若,则用“<”把连接起来。
4.若,则用“<”把连接起来。
5.若,则用“>”把连接起来。
(四)绝对值化简
1.若,则化简
2.若,则化简
3.若,则化简
4.若,则化简
5.若,则化简
6.若,则化简
7.若,则化简
(五)利用代数定义化简绝对值(数轴)
1.若,则化简.
2.若,则化简.
3.若,则化简.
4.若,则化简.
5.若,则化简.
6.若,则化简.
7.若,则化简.
8.若,则化简.
(六)零点分段(不给范围)
1.化简
2.化简
3.化简
4.求的值为常数时的范围.
(七)几何意义:分类讨论
1. 若,则=?
2. 若,则=?
3. 若,则整数解=?
4. 若,,则=?
(八)几何意义:极值问题
奇点:若含有奇数个绝对值,处于中间的零点值可以使代数式取最小值。
1. 求的最小值是多少?
2.求的最小值是多少?
3. 求的最小值是多少?
偶点:若含有偶数个绝对值,处于中间的2个零点值之间的任何一个数(包含2个零点值)都可以使可以使代数式取最小值。
4. 求的最小值是多少?
5. 求的最小值是多少?
【练习】
6. 求的最小值是多少?
7. 求的最小值是多少?
8. 若的最小值是3,则=?
9.若的最小值是5,则=?
10. 求的最大值.
11.,则的最值?
12. ,则的最值?
【考点回顾】
(1)绝对值的几何意义:一个数a的绝对值就是数轴上表示数a的点与原点的距离,数a的绝对值记作|a|.
(2)绝对值的代数意义:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.
【注意】
①取绝对值也是一种运算,运算符号是“||”,求一个数的绝对值,就是根据性质去掉绝对值符号.
②绝对值的性质:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.
③绝对值具有非负性,取绝对值的结果总是正数或0.
④任何一个有理数都是由两部分组成:符号和它的绝对值,如-5符号是负号,绝对值是5.
(3)求字母a的绝对值:
① ② ③
(4)利用绝对值比较两个负有理数的大小:两个负数,绝对值大的反而小.
(5)绝对值非负性:如果若干个非负数的和为0,那么这若干个非负数都必为0.例如:若|a|+|b|+|c|=0,则a=0,b=0,c=0.
(6)其它重要性质:
①任何一个数的绝对值都不小于这个数,也不小于这个数的相反数,即|a|≥a,且|a|≥-a;
②若|a|=|b|,则a=b或a=-b;
③;;
④|a| =|a |=a ;
⑤||a|-|b||≤|a+b|≤|a|+|b|,对于|a+b|≤|a|+|b|,等号当且仅当a、b同号或a、b中至少有一个0时,等号成立;对于||a|-|b||≤|a+b|,等号当且仅当a、b异号或a、b中至少有一个0时,等号成立.
(7)绝对值的几何意义:当x=a时,|x-a|=0,此时a是|x-a|的零点值.
|a|的几何意义:在数轴上,表示这个数的点离开原点的距离.
|a-b|的几何意义:在数轴上,表示数a、b对应数轴上两点间的距离.
【分类强化】
(一)分类讨论
1.已知,求的所有可能值。
2.已知,求的所有可能值。
3.已知,且,求的所有可能值。
4.已知,且,求的所有可能值。
5.已知,且,求的所有可能值。
6.已知,且,求的所有可能值。
7.已知,求
8.已知,求的所有可能值。
9. 已知,求的值。
10.已知,求的所有可能值。
11. 已知,求的所有可能值。
12.已知,且求=?
(二)绝对值的非负性
已知,求的值。
2.已知,求的值。
3. 已知,求的值。
4.已知与互为相反数,求得值。
5.已知,求的值。
6.若,则=?
(三)比较大小
1.若,则用“<”把连接起来。
2.若,则用“<”把连接起来。
3. 若,则用“<”把连接起来。
4.若,则用“<”把连接起来。
5.若,则用“>”把连接起来。
(四)绝对值化简
1.若,则化简
2.若,则化简
3.若,则化简
4.若,则化简
5.若,则化简
6.若,则化简
7.若,则化简
(五)利用代数定义化简绝对值(数轴)
1.若,则化简.
2.若,则化简.
3.若,则化简.
4.若,则化简.
5.若,则化简.
6.若,则化简.
7.若,则化简.
8.若,则化简.
(六)零点分段(不给范围)
1.化简
2.化简
3.化简
4.求的值为常数时的范围.
(七)几何意义:分类讨论
1. 若,则=?
2. 若,则=?
3. 若,则整数解=?
4. 若,,则=?
(八)几何意义:极值问题
奇点:若含有奇数个绝对值,处于中间的零点值可以使代数式取最小值。
1. 求的最小值是多少?
2.求的最小值是多少?
3. 求的最小值是多少?
偶点:若含有偶数个绝对值,处于中间的2个零点值之间的任何一个数(包含2个零点值)都可以使可以使代数式取最小值。
4. 求的最小值是多少?
5. 求的最小值是多少?
【练习】
6. 求的最小值是多少?
7. 求的最小值是多少?
8. 若的最小值是3,则=?
9.若的最小值是5,则=?
10. 求的最大值.
11.,则的最值?
12. ,则的最值?
