沪科版数学九年级下册第24章 圆 综合素质评价(含答案)
文档属性
| 名称 | 沪科版数学九年级下册第24章 圆 综合素质评价(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-21 00:00:00 | ||
图片预览


文档简介
第24章综合素质评价
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.下面图形中既是轴对称图形又是中心对称图形的是( )
2.【2023·广东】如图,AB是⊙O的直径,∠BAC=50°,则∠D=( )
A.20° B.40° C.50° D.80°
3.【母题:教材P57习题T5】如图所示,分别以n边形的顶点为圆心,以1 cm为半径画圆,当n=2 023时,则图中阴影部分的面积之和为( )
A.2π cm2 B.π cm2 C.2 022π cm2 D.2 023π cm2
4.在直角坐标系中,点P的坐标是(2,),⊙P的半径为2,下列说法正确的是( )
A.⊙P与x轴、y轴都有两个公共点
B.⊙P与x轴、y轴都没有公共点
C.⊙P与x轴有一个公共点,与y轴有两个公共点
D.⊙P与x轴有两个公共点,与y轴有一个公共点
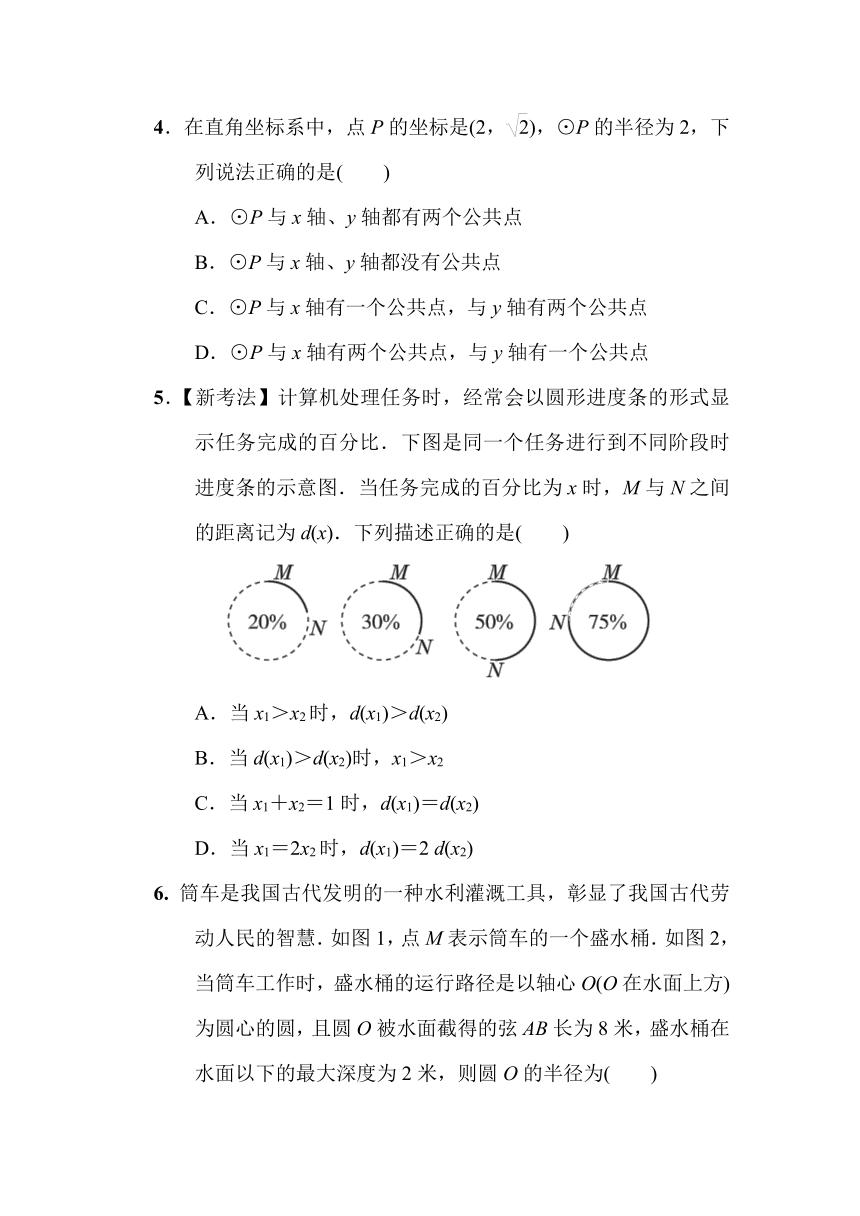
5.【新考法】计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下图是同一个任务进行到不同阶段时进度条的示意图.当任务完成的百分比为x时,M与N之间的距离记为d(x).下列描述正确的是( )
A.当x1>x2时,d(x1)>d(x2)
B.当d(x1)>d(x2)时,x1>x2
C.当x1+x2=1时,d(x1)=d(x2)
D.当x1=2x2时,d(x1)=2 d(x2)
6. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧.如图1,点M表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O(O在水面上方)为圆心的圆,且圆O被水面截得的弦AB长为8米,盛水桶在水面以下的最大深度为2米,则圆O的半径为( )
A.2米 B.3米 C.4米 D.5米
7.【易错题】在同一平面内,点P到圆上的点的最大距离为5,最小距离为1,则此圆的半径为( )
A.3 B.4或6 C.2或3 D.6
8.如图,AB是⊙O的切线,切点为点H,连接OA,OB分别与⊙O相交于点D,E,点C为⊙O上一点且∠DCE=52.5°,若⊙O的半径长为2,且∠A=30°,则AB的长为( )
A.6 B.2 +2 C.4 D.3 +2
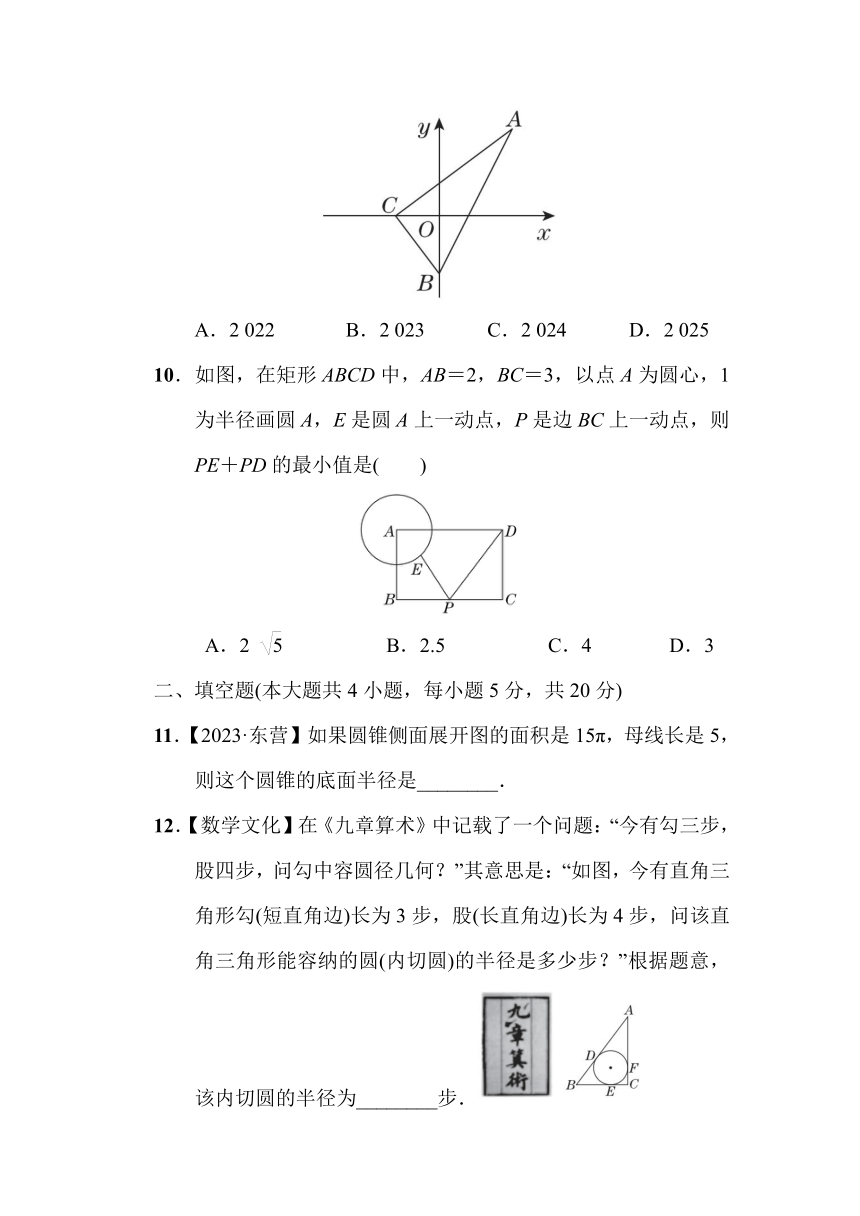
9.【2023·合肥包河区模拟】如图,在Rt△ABC中,∠ACB=90°,顶点A在第一象限,点C,B分别在x轴,y轴上,OC=3,OB=4,AC=10.将△ABC绕点O顺时针旋转,每次旋转90°,若旋转n次后点A的对应点An的坐标是(5,6),则旋转的次数可能是( )
A.2 022 B.2 023 C.2 024 D.2 025
10.如图,在矩形ABCD中,AB=2,BC=3,以点A为圆心,1为半径画圆A,E是圆A上一动点,P是边BC上一动点,则PE+PD的最小值是( )
A.2 B.2.5 C.4 D.3
二、填空题(本大题共4小题,每小题5分,共20分)
11.【2023·东营】如果圆锥侧面展开图的面积是15π,母线长是5,则这个圆锥的底面半径是________.
12.【数学文化】在《九章算术》中记载了一个问题:“今有勾三步,股四步,问勾中容圆径几何?”其意思是:“如图,今有直角三角形勾(短直角边)长为3步,股(长直角边)长为4步,问该直角三角形能容纳的圆(内切圆)的半径是多少步?”根据题意,该内切圆的半径为________步.
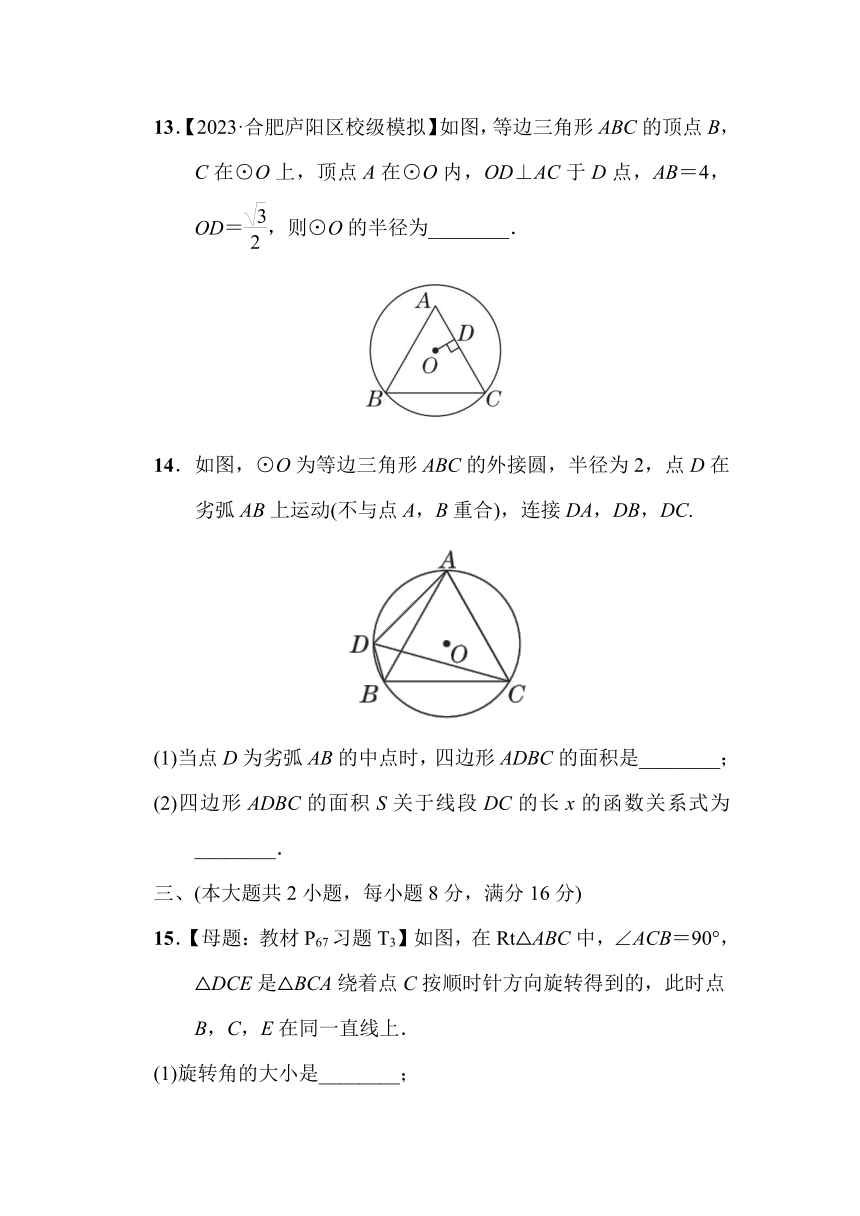
13.【2023·合肥庐阳区校级模拟】如图,等边三角形ABC的顶点B,C在⊙O上,顶点A在⊙O内,OD⊥AC于D点,AB=4,OD=,则⊙O的半径为________.
14.如图,⊙O为等边三角形ABC的外接圆,半径为2,点D在劣弧AB上运动(不与点A,B重合),连接DA,DB,DC.
(1)当点D为劣弧AB的中点时,四边形ADBC的面积是________;
(2)四边形ADBC的面积S关于线段DC的长x的函数关系式为________.
三、(本大题共2小题,每小题8分,满分16分)
15.【母题:教材P67习题T3】如图,在Rt△ABC中,∠ACB=90°,△DCE是△BCA绕着点C按顺时针方向旋转得到的,此时点B,C,E在同一直线上.
(1)旋转角的大小是________;
(2)若AB=10,AC=8,求BE的长.
16.【2023·合肥模拟】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC和格点O.
(1)将△ABC绕格点O顺时针旋转90°,得到△A1B1C1,画出△A1B1C1;
(2)以点O为对称中心,画出△ABC关于点O的中心对称图形△A2B2C2.
四、(本大题共2小题,每小题8分,满分16分)
17.【2023·合肥庐阳区模拟】如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=2,CD=8.
(1)求⊙O的半径长;
(2)连接BC,作OF⊥BC于点F,求OF的长.
18.【2023·威海】如图,在平面直角坐标系中,点P在第一象限内,⊙P与x轴相切于点C,与y轴相交于点A(0,8),B(0,2).连接AC,BC.
(1)求点P的坐标;
(2)求cos∠ACB的值.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD,垂足为点E,OF⊥AC,垂足为点F,BE=OF.
(1)求证:AC=CD;
(2)若BE=4,CD=8 ,求阴影部分的面积.
20.如图,在△ABC中,∠C=90°,AD平分∠CAB交BC于点D,AD的垂直平分线交AB于点O,以点O为圆心,以OA长为半径作⊙O,交AB于点E.
(1)求证:BC是⊙O的切线;
(2)已知BE=2,AC=4.8,求⊙O的半径.
六、(本题满分12分)
21.请阅读下面的材料,并完成相应的任务.
仅用圆规三等分、六等分圆是容易的,而四等分、五等分……则有一定难度,历史上卡尔·弗雷德里希·高斯首次解决了将圆十七等分的难题.拿破仑·波拿巴当年曾向数学家提出这样一个问题:只用圆规,不用直尺,如何把一个圆周四等分?这个难题最终由意大利数学家马斯凯罗尼解决了.为此,他还写了名为《圆规几何》的书献给拿破仑,书中还包含了更深刻的作图理论.他给出的作图步骤和部分证明如下:
如图1,第一步:在⊙O上任取一点A,以点A为一个分点,将⊙O六等分,其他分点依次为B,C,D,E,F;
第二步:分别以A,D两点为圆心,以AC(BD)为半径作弧,两弧交于点G;
第三步:以点A为圆心,OG为半径作弧,与⊙O交于M,N两点.
则点A,M,D,N是⊙O的四等分点.
证明:如图2,连接OA,OG,OC,OD,AG,AM,AC,DC,DG,DM,DN,AN.
∵点A,B,C,D,E,F是⊙O的六等分点,
∴∠COD=60°.
∴∠AOD=3∠COD=3×60°=180°.
….
任务:
(1)完成材料中的证明;
(2)若⊙O的半径为2,则OG的长为________,以点A为圆心的的长为________.
七、(本题满分12分)
22. 如图,已知四边形ABCD内接于⊙O,直径AC与弦BD交于点E,DB平分∠ADC.
(1)若AD=BD,求证:DC=DE;
(2)若=,求的值.
八、(本题满分14分)
23. 定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“伴随圆”.
(1)如图1,在△ABC中,∠C=90°,AB=5,AC=3,则BC边上的伴随圆的半径为________;
(2)如图2,在△ABC中,∠ACB=90°,点E在边AB上,AE=2BE,D为AC的中点,且∠CED=90°.
①求证:△CED的外接圆是△ABC的AC边上的伴随圆;
②的值为________.
答案
一、1.A
2.B 【点拨】∵AB是⊙O的直径,∴∠ACB=90°.∵∠BAC=50°,∴∠ABC=90°-∠BAC=40°,∴∠D=∠ABC=40°.故选B.
3.B 【点拨】由题意得,图中阴影部分的面积之和==π(cm2),故选B.
【点方法】明白阴影部分的圆心角的度数和与多边形的外角和相等是解此题的关键.
4.D 【点拨】∵P(2, ),⊙P的半径为2,∴以P为圆心,以2为半径的圆与x轴的位置关系是相交,与y轴的位置关系是相切,∴⊙P与x轴有两个公共点,与y轴有一个公共点.故选D.
5.C 【点拨】A.当x1>x2时,d(x1)与d(x2)可能相等,可能不等,本选项不符合题意.B.当d(x1)>d(x2)时,x1>x2或x1<x2,本选项不符合题意.C.当x1+x2=1时,d(x1)=d(x2),正确,本选项符合题意.D.当x1=2x2时,d(x1)<2 d(x2),本选项不符合题意.故选C.
6. D 【点拨】过点O作半径OD⊥AB交AB于点E,如图.∵AB=8米,∴AE=BE=AB=4米.由题意知DE=2米,设OD=OA=x米,则OE=(x-2)米,在Rt△AOE中,OE2+AE2=OA2,即(x-2)2+42=x2,解得x=5,故OA=5米.故选D.
7.C 【点拨】分为两种情况:①当点P在圆内时,如图1,
∵点P到圆上的点的最小距离PB=1,最大距离PA=5,∴直径AB=1+5=6,∴半径r=3;②当点P在圆外时,如图2,∵点P到圆上的点的最小距离PB=1,最大距离PA=5,∴直径AB=5-1=4,∴半径r=2.故选C.
【点易错】本题应注意分类讨论,即分点P在圆内和点P在圆外两种情况进行求解.
8.B 【点拨】如图,连接OH,∵AB是⊙O的切线,切点为H,∴OH⊥AB,∴∠AHO=∠BHO=90°.∵∠A=30°,∴OH= OA,∠AOH=60°.∵OH=2,∴OA=4.在Rt△AHO中, AH== =2.∵∠DCE=52.5°, ∴∠DOE=2∠DCE=105°,
∴∠BOH=∠DOE-∠AOH=105°-60°=45°.
∵∠BHO=90°,∴BH=2,
∴AB=AH+BH=2eq \r(3)+2,故选B.
9.C 【点拨】如图,过点A作AT⊥x轴于点T,连接OA.
∵OC=3,OB=4,∠BOC=90°,∴BC=5.∵∠ATC=∠ACB=90°,∴∠CAT+∠ACT=90°,∠ACT+∠BCO=90°,∴∠CAT=∠BCO.∴Rt△ATC∽Rt△COB,∴AT:OC=CT:OB=AC:BC,即AT:3=CT:4=10:5,∴AT=6,CT=8,∴OT=CT-OC=8-3=5,∴A(5,6).∵将△ABC绕点O顺时针旋转,每次旋转90°,∴每旋转4次点A回到原点.
∵2 024÷4=506,∴第2 024次旋转结束后,点A的对应点A2 024的坐标是(5,6),故选C.
10.C 【点拨】以BC所在直线为轴作矩形ABCD的对称图形A′BCD′,连接AD′交BC于P′,交圆A于E′,则D′E′的长就是PE+PD的最小值.∵在矩形ABCD中,AB=2,BC=3,∴A′D′=BC=3,AA′=2AB=4,∴AD′=5.
∵圆A的半径为1,∴AE′=1,∴D′E′=5-1=4,即PE+PD的最小值为4,故选C.
二、11.3 【点拨】设圆锥的底面半径为R,则底面周长=2πR,∴×2πR×5=15π,解得R=3.故这个圆锥的底面半径是3.
12.1 【点拨】如图,连接OD,OE,OF,OA,OB,OC.
∵∠BCA=90°,BC=3步,AC=4步,∴AB= ==5(步).∵D,E,F是切点,∴OD⊥AB,OE⊥BC,OF⊥AC,OD=OE=OF.∵S△ACB=·BC·AC=eq \f(1,2)·AB·OD+·BC·OE+·AC·OF,∴OE=OD=OF==1(步).
13. 【点拨】如图,作AH⊥BC于点H,连接OC,由△ABC是等边三角形,易得A,O,H三点共线,AB=BC,∠B=∠BAC=60°,BH=CH=BC=2,AH平分∠BAC,∴∠HAD=∠BAC=30°.∵OD⊥AC,∴AO=2OD=2×eq \f(,2)=eq \r(3).
∵AH=eq \f(,2)AB=eq \f(,2)×4=2,∴OH=AH-AO=eq \r(3),
∴CO== = .
14.(1)4eq \r(3)
(2)S=eq \f(,4)x2(2eq \r(3)<x≤4) 【点拨】(1)如图1,
∵△ABC是等边三角形,∴∠ABC=∠BAC=∠ACB=60°,
∴∠ADC=∠ABC=60°,∠BDC=∠BAC=60°.
∵点D是劣弧AB的中点,
∴=,∴∠ACD=∠BCD=∠ACB=30°,
∴∠DAC=∠DBC=90°,∴CD是⊙O的直径,
∴CD=4,∴AD=BD=2,BC=AC=2eq \r(3),
∴S四边形ADBC=S△ADC+S△BDC=×2×2eq \r(3)+×2×2eq \r(3)=4eq \r(3).
(2)如图2,将△ADC绕点C逆时针旋转60°,得到△BHC,
则CD=CH,∠DAC=∠HBC,
∵四边形ADBC是⊙O的内接四边形,
∴∠DAC+∠DBC=180°,∴∠DBC+∠HBC=180°,
∴点D,点B,点H三点共线.
∵DC=CH,∠CDH=∠BAC=60°,
∴△DCH是等边三角形.
∵四边形ADBC的面积S=S△ADC+S△BDC=S△CDH=eq \f(,4)CD2,∴S=eq \f(,4)x2(2eq \r(3)<x≤4).
三、15.【解】(1)90°
(2)在Rt△ABC中,
∵AB=10,AC=8,∴BC= =6.
∵△BCA绕着点C旋转得到△DCE,∴CE=CA=8,
∴BE=BC+CE=6+8=14.
16.【解】(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
四、17.【解】(1)连接OD,设⊙O的半径长为r.
∵AB⊥CD,∴∠OED=90°,DE=CE=CD=×8=4.
在Rt△ODE中,∵OE=r-2,OD=r,DE=4,
∴(r-2)2+42=r2,解得r=5,
即⊙O的半径长为5.
(2)由(1)知AB=10,在Rt△BCE中,
∵CE=4,BE=AB-AE=8,
∴BC= =4.
∵OF⊥BC,∴BF=CF=BC=2eq \r(5),∠OFB=90°,
在Rt△OBF中,OF= =eq \r(5),
即OF的长为eq \r(5).
18.【解】(1)如图,连接PC,PB,过点P作PD⊥AB,垂足为D,则BD=AB.
∵点A(0,8),B(0,2),∴OA=8,OB=2,
∴BD=AB=(OA-OB)=3,∴OD=OB+BD=5.
∵⊙P与x轴相切于点C,
∴PC=PB,∠PCO=90°.
又∵∠COD=∠PDO=90°,∴四边形OCPD是矩形,
∴PC=OD=5,∴PB=5,
在Rt△PDB中,PD===4,
∴点P的坐标为(4,5).
(2)∵PA=PB,PD⊥AB,
∴∠DPB=∠APB.
又∵∠ACB=∠APB,∴∠ACB=∠DPB.
在Rt△DPB中,cos∠DPB==,
∴cos∠ACB=.
五、19.(1)【证明】∵AB为⊙O的直径,AB⊥CD,
∴=,CE=CD,∠CEB=90°,∴∠A=∠DCB.
∵OF⊥AC,∴∠AFO=90°,AF=AC.∵BE=OF,
∴△AFO≌△CEB(AAS),∴AF=CE,∴AC=CD.
(2)【解】连接OD,∵AB为⊙O的直径,AB⊥CD,
∴CE=CD=4eq \r(3),∠COD=2∠COB,
设OC=r,则OE=r-4,
∴r2=(r-4)2+(4eq \r(3))2,解得r=8,
在Rt△OEC中,OE=8-4=4=OC,
∴∠OCE=30°,∴∠COB=60°,∴∠COD=120°,
∴S阴影=S扇形COD-S△OCD
=-×8eq \r(3)×4
=π-16eq \r(3).
20.(1)【证明】连接OD,如图,
∵AD的垂直平分线交AB于点O,∴OA=OD,
∴⊙O经过点D.
∵AD平分∠CAB,∴∠CAD=∠BAD.
∵OA=OD,∴∠BAD=∠ODA,
∴∠CAD=∠ODA,∴AC∥OD.
∵∠C=90°,∴∠ODB=∠C=90°,
∴OD⊥BC,∴BC是⊙O的切线.
(2)【解】由(1)知OD∥AC,
∴△BOD∽△BAC,∴=.
设⊙O的半径为x,则=,
解得x1=3,x2=-1.6(舍去),
经检验,x=3是原分式方程的解,
故⊙O的半径为3.
六、21.(1)【证明】∵点A,B,C,D,E,F是⊙O的六等分点,
∴∠COD=60°.∴∠AOD=3∠COD=3×60°=180°.
∴AD是⊙O的直径.∴∠ACD=90°.
∵CD=CD,∴∠CAD=∠COD=30°.
设⊙O的半径为r.
在Rt△ACD中,cos∠CAD==eq \f(,2),
∴AC=eq \r(3)r.∴AG=DG=AC=eq \r(3)r.
∵AO=OD,∴OG⊥AD.∴∠GOA=90°.
在Rt△AOG中,
OG==eq \r(( r)2-r2)=r,
∴AM=OG=eq \r(2)r.
在△AOM中,AO2+OM2=r2+r2=AM2,
∴△AOM是直角三角形且∠MOA=90°.
∴易得AM=MD=AN=DN.
∴点A,M,D,N是⊙O的四等分点.
(2)2eq \r(2);eq \r(2)π 【点拨】由(1)易得∠MAN=90°,
OG=AM=AN=2eq \r(2),
∴以点A为圆心的的长=eq \f(90π·2, 2)=eq \r(2)π.
七、22.(1)【证明】∵DB平分∠ADC,∴∠ADB=∠CDB.
在△AED和△BCD中,
∴△AED≌△BCD(ASA),∴DE=DC.
(2)【解】如图,过点B作BF⊥BD交DA的延长线于点F,即∠DBF=90°.
∵AC为⊙O的直径,∴∠ADC=∠ABC=90°.
∵DB平分∠ADC,∴∠ADB=45°.
∵∠ADB=∠ACB,∴∠ACB=45°,
∴△ABC和△BFD都为等腰直角三角形,
∴BD=BF,AB=BC.
∵∠FBD=∠ABC=90°,∴∠FBA=∠DBC.
在△ABF和△CBD中,
∴△ABF≌△CBD(SAS),
∴CD=AF.
∵=,∴设CD=AF=2k,则AD=5k,DF=7k,
在Rt△ADC中,
AC===k,
在Rt△BDF中,BD=eq \f(,2)DF=eq \f(7,2)k,
∴=eq \f(7,2)k / k=eq \f(7,58).
八、23.(1)2 【点拨】∵∠C=90°,AB=5,AC=3,
∴BC==4.
易知BC为伴随圆的直径,
∴BC边上的伴随圆的半径为2.
(2)①【证明】∵∠CED=90°,
∴△CED为直角三角形.
∴CD为△CED的外接圆的直径,且圆心O在CD的中点处.
如图,连接OE,OB.
设⊙O的半径为r,则DC=2r,AD=2r,OA=3r.
∴=.
∵EA=2BE,∴=,∴=.
∴ED∥OB.∴∠1=∠2,∠3=∠4.
又∵OD=OE,∴∠3=∠2,∴∠1=∠4.
在△BCO和△BEO中,
∴△BCO≌△BEO(SAS).∴∠BEO=∠BCO=90°.
∴AB是圆O的切线.
∴△CED的外接圆是△ABC的AC边上的伴随圆.
②eq \f(,2) 【点拨】∵在Rt△OAE中,OA=3r,OE=r,
∴EA==2eq \r(2)r.∴AB=3eq \r(2)r.
∵在Rt△ABC中,AC=4r,AB=3eq \r(2)r,
∴BC= =eq \r(2)r.
∵∠CED=∠BCO=90°,∠2=∠1,
∴△DEC∽△OCB.∴==eq \f(r,r)=eq \f(,2).
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.下面图形中既是轴对称图形又是中心对称图形的是( )
2.【2023·广东】如图,AB是⊙O的直径,∠BAC=50°,则∠D=( )
A.20° B.40° C.50° D.80°
3.【母题:教材P57习题T5】如图所示,分别以n边形的顶点为圆心,以1 cm为半径画圆,当n=2 023时,则图中阴影部分的面积之和为( )
A.2π cm2 B.π cm2 C.2 022π cm2 D.2 023π cm2
4.在直角坐标系中,点P的坐标是(2,),⊙P的半径为2,下列说法正确的是( )
A.⊙P与x轴、y轴都有两个公共点
B.⊙P与x轴、y轴都没有公共点
C.⊙P与x轴有一个公共点,与y轴有两个公共点
D.⊙P与x轴有两个公共点,与y轴有一个公共点
5.【新考法】计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下图是同一个任务进行到不同阶段时进度条的示意图.当任务完成的百分比为x时,M与N之间的距离记为d(x).下列描述正确的是( )
A.当x1>x2时,d(x1)>d(x2)
B.当d(x1)>d(x2)时,x1>x2
C.当x1+x2=1时,d(x1)=d(x2)
D.当x1=2x2时,d(x1)=2 d(x2)
6. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧.如图1,点M表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O(O在水面上方)为圆心的圆,且圆O被水面截得的弦AB长为8米,盛水桶在水面以下的最大深度为2米,则圆O的半径为( )
A.2米 B.3米 C.4米 D.5米
7.【易错题】在同一平面内,点P到圆上的点的最大距离为5,最小距离为1,则此圆的半径为( )
A.3 B.4或6 C.2或3 D.6
8.如图,AB是⊙O的切线,切点为点H,连接OA,OB分别与⊙O相交于点D,E,点C为⊙O上一点且∠DCE=52.5°,若⊙O的半径长为2,且∠A=30°,则AB的长为( )
A.6 B.2 +2 C.4 D.3 +2
9.【2023·合肥包河区模拟】如图,在Rt△ABC中,∠ACB=90°,顶点A在第一象限,点C,B分别在x轴,y轴上,OC=3,OB=4,AC=10.将△ABC绕点O顺时针旋转,每次旋转90°,若旋转n次后点A的对应点An的坐标是(5,6),则旋转的次数可能是( )
A.2 022 B.2 023 C.2 024 D.2 025
10.如图,在矩形ABCD中,AB=2,BC=3,以点A为圆心,1为半径画圆A,E是圆A上一动点,P是边BC上一动点,则PE+PD的最小值是( )
A.2 B.2.5 C.4 D.3
二、填空题(本大题共4小题,每小题5分,共20分)
11.【2023·东营】如果圆锥侧面展开图的面积是15π,母线长是5,则这个圆锥的底面半径是________.
12.【数学文化】在《九章算术》中记载了一个问题:“今有勾三步,股四步,问勾中容圆径几何?”其意思是:“如图,今有直角三角形勾(短直角边)长为3步,股(长直角边)长为4步,问该直角三角形能容纳的圆(内切圆)的半径是多少步?”根据题意,该内切圆的半径为________步.
13.【2023·合肥庐阳区校级模拟】如图,等边三角形ABC的顶点B,C在⊙O上,顶点A在⊙O内,OD⊥AC于D点,AB=4,OD=,则⊙O的半径为________.
14.如图,⊙O为等边三角形ABC的外接圆,半径为2,点D在劣弧AB上运动(不与点A,B重合),连接DA,DB,DC.
(1)当点D为劣弧AB的中点时,四边形ADBC的面积是________;
(2)四边形ADBC的面积S关于线段DC的长x的函数关系式为________.
三、(本大题共2小题,每小题8分,满分16分)
15.【母题:教材P67习题T3】如图,在Rt△ABC中,∠ACB=90°,△DCE是△BCA绕着点C按顺时针方向旋转得到的,此时点B,C,E在同一直线上.
(1)旋转角的大小是________;
(2)若AB=10,AC=8,求BE的长.
16.【2023·合肥模拟】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC和格点O.
(1)将△ABC绕格点O顺时针旋转90°,得到△A1B1C1,画出△A1B1C1;
(2)以点O为对称中心,画出△ABC关于点O的中心对称图形△A2B2C2.
四、(本大题共2小题,每小题8分,满分16分)
17.【2023·合肥庐阳区模拟】如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=2,CD=8.
(1)求⊙O的半径长;
(2)连接BC,作OF⊥BC于点F,求OF的长.
18.【2023·威海】如图,在平面直角坐标系中,点P在第一象限内,⊙P与x轴相切于点C,与y轴相交于点A(0,8),B(0,2).连接AC,BC.
(1)求点P的坐标;
(2)求cos∠ACB的值.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD,垂足为点E,OF⊥AC,垂足为点F,BE=OF.
(1)求证:AC=CD;
(2)若BE=4,CD=8 ,求阴影部分的面积.
20.如图,在△ABC中,∠C=90°,AD平分∠CAB交BC于点D,AD的垂直平分线交AB于点O,以点O为圆心,以OA长为半径作⊙O,交AB于点E.
(1)求证:BC是⊙O的切线;
(2)已知BE=2,AC=4.8,求⊙O的半径.
六、(本题满分12分)
21.请阅读下面的材料,并完成相应的任务.
仅用圆规三等分、六等分圆是容易的,而四等分、五等分……则有一定难度,历史上卡尔·弗雷德里希·高斯首次解决了将圆十七等分的难题.拿破仑·波拿巴当年曾向数学家提出这样一个问题:只用圆规,不用直尺,如何把一个圆周四等分?这个难题最终由意大利数学家马斯凯罗尼解决了.为此,他还写了名为《圆规几何》的书献给拿破仑,书中还包含了更深刻的作图理论.他给出的作图步骤和部分证明如下:
如图1,第一步:在⊙O上任取一点A,以点A为一个分点,将⊙O六等分,其他分点依次为B,C,D,E,F;
第二步:分别以A,D两点为圆心,以AC(BD)为半径作弧,两弧交于点G;
第三步:以点A为圆心,OG为半径作弧,与⊙O交于M,N两点.
则点A,M,D,N是⊙O的四等分点.
证明:如图2,连接OA,OG,OC,OD,AG,AM,AC,DC,DG,DM,DN,AN.
∵点A,B,C,D,E,F是⊙O的六等分点,
∴∠COD=60°.
∴∠AOD=3∠COD=3×60°=180°.
….
任务:
(1)完成材料中的证明;
(2)若⊙O的半径为2,则OG的长为________,以点A为圆心的的长为________.
七、(本题满分12分)
22. 如图,已知四边形ABCD内接于⊙O,直径AC与弦BD交于点E,DB平分∠ADC.
(1)若AD=BD,求证:DC=DE;
(2)若=,求的值.
八、(本题满分14分)
23. 定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“伴随圆”.
(1)如图1,在△ABC中,∠C=90°,AB=5,AC=3,则BC边上的伴随圆的半径为________;
(2)如图2,在△ABC中,∠ACB=90°,点E在边AB上,AE=2BE,D为AC的中点,且∠CED=90°.
①求证:△CED的外接圆是△ABC的AC边上的伴随圆;
②的值为________.
答案
一、1.A
2.B 【点拨】∵AB是⊙O的直径,∴∠ACB=90°.∵∠BAC=50°,∴∠ABC=90°-∠BAC=40°,∴∠D=∠ABC=40°.故选B.
3.B 【点拨】由题意得,图中阴影部分的面积之和==π(cm2),故选B.
【点方法】明白阴影部分的圆心角的度数和与多边形的外角和相等是解此题的关键.
4.D 【点拨】∵P(2, ),⊙P的半径为2,∴以P为圆心,以2为半径的圆与x轴的位置关系是相交,与y轴的位置关系是相切,∴⊙P与x轴有两个公共点,与y轴有一个公共点.故选D.
5.C 【点拨】A.当x1>x2时,d(x1)与d(x2)可能相等,可能不等,本选项不符合题意.B.当d(x1)>d(x2)时,x1>x2或x1<x2,本选项不符合题意.C.当x1+x2=1时,d(x1)=d(x2),正确,本选项符合题意.D.当x1=2x2时,d(x1)<2 d(x2),本选项不符合题意.故选C.
6. D 【点拨】过点O作半径OD⊥AB交AB于点E,如图.∵AB=8米,∴AE=BE=AB=4米.由题意知DE=2米,设OD=OA=x米,则OE=(x-2)米,在Rt△AOE中,OE2+AE2=OA2,即(x-2)2+42=x2,解得x=5,故OA=5米.故选D.
7.C 【点拨】分为两种情况:①当点P在圆内时,如图1,
∵点P到圆上的点的最小距离PB=1,最大距离PA=5,∴直径AB=1+5=6,∴半径r=3;②当点P在圆外时,如图2,∵点P到圆上的点的最小距离PB=1,最大距离PA=5,∴直径AB=5-1=4,∴半径r=2.故选C.
【点易错】本题应注意分类讨论,即分点P在圆内和点P在圆外两种情况进行求解.
8.B 【点拨】如图,连接OH,∵AB是⊙O的切线,切点为H,∴OH⊥AB,∴∠AHO=∠BHO=90°.∵∠A=30°,∴OH= OA,∠AOH=60°.∵OH=2,∴OA=4.在Rt△AHO中, AH== =2.∵∠DCE=52.5°, ∴∠DOE=2∠DCE=105°,
∴∠BOH=∠DOE-∠AOH=105°-60°=45°.
∵∠BHO=90°,∴BH=2,
∴AB=AH+BH=2eq \r(3)+2,故选B.
9.C 【点拨】如图,过点A作AT⊥x轴于点T,连接OA.
∵OC=3,OB=4,∠BOC=90°,∴BC=5.∵∠ATC=∠ACB=90°,∴∠CAT+∠ACT=90°,∠ACT+∠BCO=90°,∴∠CAT=∠BCO.∴Rt△ATC∽Rt△COB,∴AT:OC=CT:OB=AC:BC,即AT:3=CT:4=10:5,∴AT=6,CT=8,∴OT=CT-OC=8-3=5,∴A(5,6).∵将△ABC绕点O顺时针旋转,每次旋转90°,∴每旋转4次点A回到原点.
∵2 024÷4=506,∴第2 024次旋转结束后,点A的对应点A2 024的坐标是(5,6),故选C.
10.C 【点拨】以BC所在直线为轴作矩形ABCD的对称图形A′BCD′,连接AD′交BC于P′,交圆A于E′,则D′E′的长就是PE+PD的最小值.∵在矩形ABCD中,AB=2,BC=3,∴A′D′=BC=3,AA′=2AB=4,∴AD′=5.
∵圆A的半径为1,∴AE′=1,∴D′E′=5-1=4,即PE+PD的最小值为4,故选C.
二、11.3 【点拨】设圆锥的底面半径为R,则底面周长=2πR,∴×2πR×5=15π,解得R=3.故这个圆锥的底面半径是3.
12.1 【点拨】如图,连接OD,OE,OF,OA,OB,OC.
∵∠BCA=90°,BC=3步,AC=4步,∴AB= ==5(步).∵D,E,F是切点,∴OD⊥AB,OE⊥BC,OF⊥AC,OD=OE=OF.∵S△ACB=·BC·AC=eq \f(1,2)·AB·OD+·BC·OE+·AC·OF,∴OE=OD=OF==1(步).
13. 【点拨】如图,作AH⊥BC于点H,连接OC,由△ABC是等边三角形,易得A,O,H三点共线,AB=BC,∠B=∠BAC=60°,BH=CH=BC=2,AH平分∠BAC,∴∠HAD=∠BAC=30°.∵OD⊥AC,∴AO=2OD=2×eq \f(,2)=eq \r(3).
∵AH=eq \f(,2)AB=eq \f(,2)×4=2,∴OH=AH-AO=eq \r(3),
∴CO== = .
14.(1)4eq \r(3)
(2)S=eq \f(,4)x2(2eq \r(3)<x≤4) 【点拨】(1)如图1,
∵△ABC是等边三角形,∴∠ABC=∠BAC=∠ACB=60°,
∴∠ADC=∠ABC=60°,∠BDC=∠BAC=60°.
∵点D是劣弧AB的中点,
∴=,∴∠ACD=∠BCD=∠ACB=30°,
∴∠DAC=∠DBC=90°,∴CD是⊙O的直径,
∴CD=4,∴AD=BD=2,BC=AC=2eq \r(3),
∴S四边形ADBC=S△ADC+S△BDC=×2×2eq \r(3)+×2×2eq \r(3)=4eq \r(3).
(2)如图2,将△ADC绕点C逆时针旋转60°,得到△BHC,
则CD=CH,∠DAC=∠HBC,
∵四边形ADBC是⊙O的内接四边形,
∴∠DAC+∠DBC=180°,∴∠DBC+∠HBC=180°,
∴点D,点B,点H三点共线.
∵DC=CH,∠CDH=∠BAC=60°,
∴△DCH是等边三角形.
∵四边形ADBC的面积S=S△ADC+S△BDC=S△CDH=eq \f(,4)CD2,∴S=eq \f(,4)x2(2eq \r(3)<x≤4).
三、15.【解】(1)90°
(2)在Rt△ABC中,
∵AB=10,AC=8,∴BC= =6.
∵△BCA绕着点C旋转得到△DCE,∴CE=CA=8,
∴BE=BC+CE=6+8=14.
16.【解】(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
四、17.【解】(1)连接OD,设⊙O的半径长为r.
∵AB⊥CD,∴∠OED=90°,DE=CE=CD=×8=4.
在Rt△ODE中,∵OE=r-2,OD=r,DE=4,
∴(r-2)2+42=r2,解得r=5,
即⊙O的半径长为5.
(2)由(1)知AB=10,在Rt△BCE中,
∵CE=4,BE=AB-AE=8,
∴BC= =4.
∵OF⊥BC,∴BF=CF=BC=2eq \r(5),∠OFB=90°,
在Rt△OBF中,OF= =eq \r(5),
即OF的长为eq \r(5).
18.【解】(1)如图,连接PC,PB,过点P作PD⊥AB,垂足为D,则BD=AB.
∵点A(0,8),B(0,2),∴OA=8,OB=2,
∴BD=AB=(OA-OB)=3,∴OD=OB+BD=5.
∵⊙P与x轴相切于点C,
∴PC=PB,∠PCO=90°.
又∵∠COD=∠PDO=90°,∴四边形OCPD是矩形,
∴PC=OD=5,∴PB=5,
在Rt△PDB中,PD===4,
∴点P的坐标为(4,5).
(2)∵PA=PB,PD⊥AB,
∴∠DPB=∠APB.
又∵∠ACB=∠APB,∴∠ACB=∠DPB.
在Rt△DPB中,cos∠DPB==,
∴cos∠ACB=.
五、19.(1)【证明】∵AB为⊙O的直径,AB⊥CD,
∴=,CE=CD,∠CEB=90°,∴∠A=∠DCB.
∵OF⊥AC,∴∠AFO=90°,AF=AC.∵BE=OF,
∴△AFO≌△CEB(AAS),∴AF=CE,∴AC=CD.
(2)【解】连接OD,∵AB为⊙O的直径,AB⊥CD,
∴CE=CD=4eq \r(3),∠COD=2∠COB,
设OC=r,则OE=r-4,
∴r2=(r-4)2+(4eq \r(3))2,解得r=8,
在Rt△OEC中,OE=8-4=4=OC,
∴∠OCE=30°,∴∠COB=60°,∴∠COD=120°,
∴S阴影=S扇形COD-S△OCD
=-×8eq \r(3)×4
=π-16eq \r(3).
20.(1)【证明】连接OD,如图,
∵AD的垂直平分线交AB于点O,∴OA=OD,
∴⊙O经过点D.
∵AD平分∠CAB,∴∠CAD=∠BAD.
∵OA=OD,∴∠BAD=∠ODA,
∴∠CAD=∠ODA,∴AC∥OD.
∵∠C=90°,∴∠ODB=∠C=90°,
∴OD⊥BC,∴BC是⊙O的切线.
(2)【解】由(1)知OD∥AC,
∴△BOD∽△BAC,∴=.
设⊙O的半径为x,则=,
解得x1=3,x2=-1.6(舍去),
经检验,x=3是原分式方程的解,
故⊙O的半径为3.
六、21.(1)【证明】∵点A,B,C,D,E,F是⊙O的六等分点,
∴∠COD=60°.∴∠AOD=3∠COD=3×60°=180°.
∴AD是⊙O的直径.∴∠ACD=90°.
∵CD=CD,∴∠CAD=∠COD=30°.
设⊙O的半径为r.
在Rt△ACD中,cos∠CAD==eq \f(,2),
∴AC=eq \r(3)r.∴AG=DG=AC=eq \r(3)r.
∵AO=OD,∴OG⊥AD.∴∠GOA=90°.
在Rt△AOG中,
OG==eq \r(( r)2-r2)=r,
∴AM=OG=eq \r(2)r.
在△AOM中,AO2+OM2=r2+r2=AM2,
∴△AOM是直角三角形且∠MOA=90°.
∴易得AM=MD=AN=DN.
∴点A,M,D,N是⊙O的四等分点.
(2)2eq \r(2);eq \r(2)π 【点拨】由(1)易得∠MAN=90°,
OG=AM=AN=2eq \r(2),
∴以点A为圆心的的长=eq \f(90π·2, 2)=eq \r(2)π.
七、22.(1)【证明】∵DB平分∠ADC,∴∠ADB=∠CDB.
在△AED和△BCD中,
∴△AED≌△BCD(ASA),∴DE=DC.
(2)【解】如图,过点B作BF⊥BD交DA的延长线于点F,即∠DBF=90°.
∵AC为⊙O的直径,∴∠ADC=∠ABC=90°.
∵DB平分∠ADC,∴∠ADB=45°.
∵∠ADB=∠ACB,∴∠ACB=45°,
∴△ABC和△BFD都为等腰直角三角形,
∴BD=BF,AB=BC.
∵∠FBD=∠ABC=90°,∴∠FBA=∠DBC.
在△ABF和△CBD中,
∴△ABF≌△CBD(SAS),
∴CD=AF.
∵=,∴设CD=AF=2k,则AD=5k,DF=7k,
在Rt△ADC中,
AC===k,
在Rt△BDF中,BD=eq \f(,2)DF=eq \f(7,2)k,
∴=eq \f(7,2)k / k=eq \f(7,58).
八、23.(1)2 【点拨】∵∠C=90°,AB=5,AC=3,
∴BC==4.
易知BC为伴随圆的直径,
∴BC边上的伴随圆的半径为2.
(2)①【证明】∵∠CED=90°,
∴△CED为直角三角形.
∴CD为△CED的外接圆的直径,且圆心O在CD的中点处.
如图,连接OE,OB.
设⊙O的半径为r,则DC=2r,AD=2r,OA=3r.
∴=.
∵EA=2BE,∴=,∴=.
∴ED∥OB.∴∠1=∠2,∠3=∠4.
又∵OD=OE,∴∠3=∠2,∴∠1=∠4.
在△BCO和△BEO中,
∴△BCO≌△BEO(SAS).∴∠BEO=∠BCO=90°.
∴AB是圆O的切线.
∴△CED的外接圆是△ABC的AC边上的伴随圆.
②eq \f(,2) 【点拨】∵在Rt△OAE中,OA=3r,OE=r,
∴EA==2eq \r(2)r.∴AB=3eq \r(2)r.
∵在Rt△ABC中,AC=4r,AB=3eq \r(2)r,
∴BC= =eq \r(2)r.
∵∠CED=∠BCO=90°,∠2=∠1,
∴△DEC∽△OCB.∴==eq \f(r,r)=eq \f(,2).
