2023-2024学年冀教版数学九年级上册单元闯关双测卷第二十三章 数据分析(测基础)(含解析)
文档属性
| 名称 | 2023-2024学年冀教版数学九年级上册单元闯关双测卷第二十三章 数据分析(测基础)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 250.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 20:24:57 | ||
图片预览




文档简介
第二十三章 数据分析
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.某校组织环保知识竞赛,为参加区级比赛做选手选拔工作,经过多次测试后,有4名同学成为区级参赛选手的候选人,具体情况如表:
甲 乙 丙 丁
平均分 90 92 95 95
方差 36 32 21 33
如果从这4名同学中选出1位参加区级比赛(总体水平高且状态稳定),你会推荐( )
A.甲 B.乙 C.丙 D.丁
2.一组数据为4,2,a,5,1,若这组数据的平均数为3,则a的值为( )
A.2 B.3 C.4 D.5
3.某班的一节体育课上,老师组织部分男同学进行了投篮比赛,每人投10次,参赛的同学投中的次数如表所示,则他们投中次数的中位数和众数分别是( )
投中次数 6 7 8 9
人数人 2 2 3 1
A.2,3 B.7,4.5 C.7.5,8 D.7,8
4.五月是水蜜桃盛产的季节,如图是小华前三次购买水蜜桃单价的单价的统计图,第四次买的水蜜桃单价是a元/千克,若这四个单价的中位数恰好也是众数,则a的值是( )
A.6 B.7 C.8 D.9
5.已知一组数据1,3,0,x,2,2,3有唯一的众数3,则这组数据的平均数中位数分别是( )
A.2,3 B.3,2 C.2,2 D.3,3
6.对于一组数据﹣1、4、﹣1、2下列结论不正确的是( )
A.平均数是1 B.众数是-1 C.中位数是0.5 D.方差是3.5
7.小明参加校园歌手比赛80分,音乐知识100分,综合知识90分,学校按唱功:音乐知识:综合知识6:2:2的比例计算总成绩为,小明的总成绩是( )
A.86 B.88 C.87 D.93
8.如图是某班甲、乙、丙三名同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( )
A.甲的数学成绩高于班级平均分,且成绩比较稳定
B.乙的数学成绩在班级平均分附近波动,且比丙好
C.丙的数学成绩低于班级平均分,但成绩逐次提高
D.就甲、乙、丙三个人而言,乙的数学成绩最不稳定
9.数据6,8,9中添加一个数据a后,发现这组新数据的中位数恰好也是众数,则a的值为( )
A.9 B.8 C.7 D.6
10.某轮滑队所有队员的年龄只有12、13、14、15、16(岁)五种情况,其中部分数据如图所示,若队员年龄的唯一的众数与中位数相等,则这个轮滑队队员人数m最小是( )
A.9 B.10 C.11 D.12
二、填空题(每小题4分,共20分)
11.第19届亚运会将在杭州举办,某射箭运动员在富阳射击射箭馆进行训练,他连续射靶5次,所得环数分别是:8,6,10,7,9,则这运动员所得环数的平均数为______.
12.甲、乙两名同学进行投掷实心球测试,每人10次投掷实心球成绩的平均数相等,方差分别为,,则甲、乙两名同学投掷实心球成绩比较稳定的是______填“甲”或“乙”
13.已知一组数据2,2,8,x,7,4的中位数为5,则x的值是_________.
14.一列数据:1,2,3,x,5,5的平均数是4,则这组数据的中位数是______.
15.如果一组数据为4,a,5,3,8,其平均数为a,那么这组数据的方差为__________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)我市某中学举行十佳歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据所给信息填空:
平均数(分) 中位数(分) 众数(分) 方差
初中部 85 ______ 85 _______
高中部 _____ 80 ______ 160
(2)你觉得高中部和初中部的决赛成绩哪个更好?说明理由.
17.(8分)随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(3)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图,请根据以上信息回答:
(1)该班所抢红包金额的众数是______,中位数是______;
(2)该班同学所抢红包的平均金额是多少元?
(3)若该校共有22个班级,平均每班50人,请你估计该校学生春节期间所抢的红包总金额为多少元?
18.(10分)期中考试中,A,B,C,D,E五位同学的数学、英语成绩有如下表所示的信息:
A B C D E 平均分 中位数
数学 71 72 69 68 70
英语 88 82 94 85 76
(1)完成表格中的数据;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩方差.
从标准分看,标准分高的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
19.(10分)某公司为了了解员工每人所创年利润情况,公司从各部抽取部分员工对每年所创利润进行统计,并绘制如图1,图2统计图.
________
(1)将图2补充完整;
(2)本次共抽取员工________人,每人所创年利润的众数是________万元,平均数是________万元,中位数是________万元;
(3)若每人创造年利润10万元及(含10万元)以上为优秀员工,在公司1200员工中有多少可以评为优秀员工
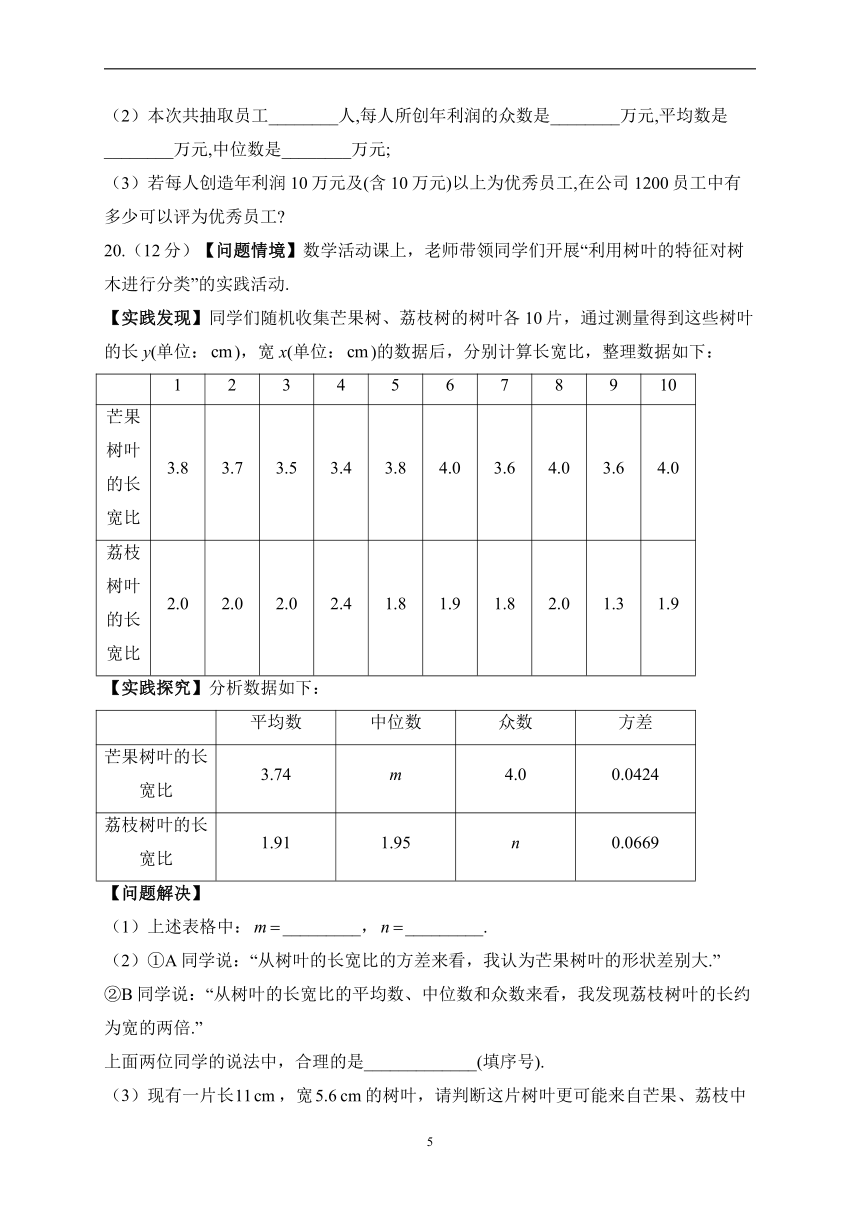
20.(12分)【问题情境】数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动.
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片,通过测量得到这些树叶的长y(单位:),宽x(单位:)的数据后,分别计算长宽比,整理数据如下:
1 2 3 4 5 6 7 8 9 10
芒果树叶的长宽比 3.8 3.7 3.5 3.4 3.8 4.0 3.6 4.0 3.6 4.0
荔枝树叶的长宽比 2.0 2.0 2.0 2.4 1.8 1.9 1.8 2.0 1.3 1.9
【实践探究】分析数据如下:
平均数 中位数 众数 方差
芒果树叶的长宽比 3.74 m 4.0 0.0424
荔枝树叶的长宽比 1.91 1.95 n 0.0669
【问题解决】
(1)上述表格中:_________,_________.
(2)①A同学说:“从树叶的长宽比的方差来看,我认为芒果树叶的形状差别大.”
②B同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的两倍.”
上面两位同学的说法中,合理的是_____________(填序号).
(3)现有一片长,宽的树叶,请判断这片树叶更可能来自芒果、荔枝中的哪种树,并给出你的理由.
21.(12分)为进一步宣传防溺水知识,提高学生防溺水的能力,某校组织七、八年级各200名学生进行防溺水知识竞赛(满分100分).现分别在七、八年级中各随机抽取10名学生的测试成绩x(单位:分)进行统计、整理如下:
七年级:86,90,79,84,74,93,76,81,90,87.
八年级:85,76,90,81,84,92,81,84,83,84.
七、八年级测试成绩频数统计表
七年级 3 4 3
八年级 1 7 a
七、八年级测试成绩分析统计表
平均数 中位数 众数 方差
七年级 84 b 90 36.4
八年级 84 84 c 18.4
根据以上信息,解答下列问题:
(1)___________,__________,__________;
(2)按学生的实际成绩,你认为哪个年级的学生掌握防溺水知识的总体水平较好 请说明理由.
(3)如果把的记为“优秀”,把的记为“合格”,学校规定两项成绩按6:4计算,通过计算比较哪个年级得分较高
答案以及解析
1.答案:C
解析:由于丙的方差较小,平均数较大,则应推荐丙.
故选:C.
2.答案:B
解析:一组数据为4,2,a,5,1,这组数据的平均数为3,
这组数据之和为:,
,
故选:B.
3.答案:C
解析:把投中的次数按从小到大排列6,6,7,7,8,8,8,9,处于中间的两个数是7与8,7与8的平均数为7.5,所以投中次数的中位数为7.5;
因为众数是出现频数最高的数据,投中次数是8次的人数有3人,最多,故投中次数的众数是8.
故选:C.
4.答案:C
解析:由统计图可知,前三次的中位数是8,
第四次买的水蜜桃单价是a元/千克,这四个单价的中位数恰好也是众数,
,
故选C.
5.答案:C
解析:这组数据有唯一的众数3,
,
将数据从小到大排列为:0,1,2,2,3,3,3,
则平均数,
中位数为:2.
故选:C.
6.答案:D
解析:这组数据的平均数是:;
-1出现了2次,出现的次数最多,则众数是-1;
把这组数据从小到大排列为:-1,-1,2,4,最中间的数是第2、3个数的平均数,则中位数是;
这组数据的方差是:;
故选D.
7.答案:A
解析:小明的总评成绩是:
(分).
故选:A.
8.答案:D
解析:A.甲的数学成绩高于班级平均分,且成绩比较稳定,故A选项正确;
B.乙的数学成绩在班级平均分附近波动,且比丙好,故B选项正确;
C.丙的数学成绩低于班级平均分,但成绩逐次提高,故C选项正确;
D.就甲、乙、丙三个人而言,丙的数学成绩最不稳定,故D选项错误.
9.答案:B
解析:中位数与8有关,且添加一个数据a后这组新数据的中位数恰好也是众数,
这组新数据的中位数和众数都是8,
,.故选B.
10.答案:D
解析:由图中数据可知小于14的4人,大于14的也是4人,
这组数据的中位数为14,
队员年龄的唯一的众数与中位数相等,
众数是14,即年龄为14的人最多,
14岁的队员最少有4人.
这个轮滑队队员人数m最小值,
故选:D.
11.答案:8环
解析:这运动员所得环数的平均数为环,
故答案为:8环.
12.答案:甲
解析:因为,
方差小的为甲,
所以甲、乙两名同学投掷实心球成绩比较稳定的是甲.
故答案为:甲.
13.答案:6
解析:因为这组数据共有6个数,
所以将其按从小到大进行排序后,第3个数和第4个数的平均数即为中位数,
又因为这组数据的中位数为5,
所以第3个数和第4个数的和为,
所以只能是,
解得,
故答案为:6.
14.答案:4
解析:由题意知,,
解得,
这组数据为1,2,3,5,5,8,
这组数据的中位数是,
故答案为:4.
15.答案:2.8
解析:因为这组数据4,a,5,3,8的平均数为a,所以,解得,故这组数据的方差.
16.答案:(1)85,70,85,100
(2)初中部的成绩更好,理由见解析
解析:(1)根据统计图可得初中部5位选手的成绩从小到大排列为:75,80,85,85,100
高中部5位选手的成绩从小到大排列为:70,75,80,100,100
故初中部的中位数为:85(分);
方差为;
高中部的平均数为(分);
众数为100(分);
故填表如下:
平均数(分) 中位数(分) 众数(分) 方差
初中部 85 85 85 70
高中部 85 80 100 160
故答案为:85,70,85,100.
(2)答:我觉得初中部的成绩更好,因为初中部和高中部的成绩平均数一样,但是初中部的方差比高中部小,成绩更整齐.
17.答案:(1)30元,30元;
(2)32.4元;
(3)35640元;
解析:(1)根据统计图可知金额为30元的有20名学生为最多,即可知众数为30元.
根据统计图可知按金额从小到大排列,50名学生中,第25和26名学生的金额都为30元,即可知中位数为30元.
故答案为30元,30元;
(2)(元)
故该班同学所抢红包的平均金额是32.4元;
(3)(元)
故该校学生春节期间所抢的红包总金额约为35640元.
18.答案:(1)数学平均分是(分),中位数为70分;
英语平均分是(分),
中位数为85分.故答案为70,70,85,85.
(2)数学成绩的方差为,
英语成绩的方差为.
A同学数学标准分为,
A同学英语标准分为,
因为,
所以A同学在本次考试中,数学学科考得更好.
19.
解析:(1)
(2)抽取员工总数为:(人)
每人所创年利润的众数是8万元,
平均数是:万元
(3)(人)
答:在公司1200员工中有384人可以评为优秀员工.
20.(1)答案:3.75;2.0
解析:把芒果树叶的长宽比按照从小到大的顺序排列为3.4,3.5,3.6,3.6,3.7,3.8,3.8,4.0,4.0,4.0,第5,6位的数分别为3.7,3.8,
中位数为,;
荔枝树叶的长宽比数据中,2.0出现了4次,出现的次数最多,
众数是2.0,.
(2)答案:②
解析:从树叶的长宽比的方差来看,芒果树叶的长宽比的方差较小,所以芒果树叶的形状差别较小;从树叶的长宽比的平均数、中位数和众数来看,荔枝树叶的长约为宽的两倍.
(3)答案:这片树叶更可能来自荔枝树.理由见解析
解析:这片树叶更可能来自荔枝树.理由如下:
,
结合两种树叶的长宽比的平均数、中位数和众数,可知这片树叶更可能来自荔枝树.
21.答案:(1)2,85,84;
(2)八年级,理由见解析;
(3)七年级得分较高;
解析:(1),
根据众数的定义可知,,
把七年级10名学生的测试成绩按从小到大的顺序排
列为74,76,79,81,84,86,87,90,90,93,
根据中位数的定义可知,该组数据的中位数为,故.
(2)八年级学生掌握防溺水知识的总体水平较好,理由:七、八年级成绩的平均数相等,但八年级成绩的方差小于七年级成绩的方差,所以八年级学生掌握防溺水知识的总体水平较好.
(3)七年级得分:,
八年级得分:,
因为,所以七年级得分较高.
2
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.某校组织环保知识竞赛,为参加区级比赛做选手选拔工作,经过多次测试后,有4名同学成为区级参赛选手的候选人,具体情况如表:
甲 乙 丙 丁
平均分 90 92 95 95
方差 36 32 21 33
如果从这4名同学中选出1位参加区级比赛(总体水平高且状态稳定),你会推荐( )
A.甲 B.乙 C.丙 D.丁
2.一组数据为4,2,a,5,1,若这组数据的平均数为3,则a的值为( )
A.2 B.3 C.4 D.5
3.某班的一节体育课上,老师组织部分男同学进行了投篮比赛,每人投10次,参赛的同学投中的次数如表所示,则他们投中次数的中位数和众数分别是( )
投中次数 6 7 8 9
人数人 2 2 3 1
A.2,3 B.7,4.5 C.7.5,8 D.7,8
4.五月是水蜜桃盛产的季节,如图是小华前三次购买水蜜桃单价的单价的统计图,第四次买的水蜜桃单价是a元/千克,若这四个单价的中位数恰好也是众数,则a的值是( )
A.6 B.7 C.8 D.9
5.已知一组数据1,3,0,x,2,2,3有唯一的众数3,则这组数据的平均数中位数分别是( )
A.2,3 B.3,2 C.2,2 D.3,3
6.对于一组数据﹣1、4、﹣1、2下列结论不正确的是( )
A.平均数是1 B.众数是-1 C.中位数是0.5 D.方差是3.5
7.小明参加校园歌手比赛80分,音乐知识100分,综合知识90分,学校按唱功:音乐知识:综合知识6:2:2的比例计算总成绩为,小明的总成绩是( )
A.86 B.88 C.87 D.93
8.如图是某班甲、乙、丙三名同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( )
A.甲的数学成绩高于班级平均分,且成绩比较稳定
B.乙的数学成绩在班级平均分附近波动,且比丙好
C.丙的数学成绩低于班级平均分,但成绩逐次提高
D.就甲、乙、丙三个人而言,乙的数学成绩最不稳定
9.数据6,8,9中添加一个数据a后,发现这组新数据的中位数恰好也是众数,则a的值为( )
A.9 B.8 C.7 D.6
10.某轮滑队所有队员的年龄只有12、13、14、15、16(岁)五种情况,其中部分数据如图所示,若队员年龄的唯一的众数与中位数相等,则这个轮滑队队员人数m最小是( )
A.9 B.10 C.11 D.12
二、填空题(每小题4分,共20分)
11.第19届亚运会将在杭州举办,某射箭运动员在富阳射击射箭馆进行训练,他连续射靶5次,所得环数分别是:8,6,10,7,9,则这运动员所得环数的平均数为______.
12.甲、乙两名同学进行投掷实心球测试,每人10次投掷实心球成绩的平均数相等,方差分别为,,则甲、乙两名同学投掷实心球成绩比较稳定的是______填“甲”或“乙”
13.已知一组数据2,2,8,x,7,4的中位数为5,则x的值是_________.
14.一列数据:1,2,3,x,5,5的平均数是4,则这组数据的中位数是______.
15.如果一组数据为4,a,5,3,8,其平均数为a,那么这组数据的方差为__________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)我市某中学举行十佳歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据所给信息填空:
平均数(分) 中位数(分) 众数(分) 方差
初中部 85 ______ 85 _______
高中部 _____ 80 ______ 160
(2)你觉得高中部和初中部的决赛成绩哪个更好?说明理由.
17.(8分)随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(3)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图,请根据以上信息回答:
(1)该班所抢红包金额的众数是______,中位数是______;
(2)该班同学所抢红包的平均金额是多少元?
(3)若该校共有22个班级,平均每班50人,请你估计该校学生春节期间所抢的红包总金额为多少元?
18.(10分)期中考试中,A,B,C,D,E五位同学的数学、英语成绩有如下表所示的信息:
A B C D E 平均分 中位数
数学 71 72 69 68 70
英语 88 82 94 85 76
(1)完成表格中的数据;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩方差.
从标准分看,标准分高的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
19.(10分)某公司为了了解员工每人所创年利润情况,公司从各部抽取部分员工对每年所创利润进行统计,并绘制如图1,图2统计图.
________
(1)将图2补充完整;
(2)本次共抽取员工________人,每人所创年利润的众数是________万元,平均数是________万元,中位数是________万元;
(3)若每人创造年利润10万元及(含10万元)以上为优秀员工,在公司1200员工中有多少可以评为优秀员工
20.(12分)【问题情境】数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动.
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片,通过测量得到这些树叶的长y(单位:),宽x(单位:)的数据后,分别计算长宽比,整理数据如下:
1 2 3 4 5 6 7 8 9 10
芒果树叶的长宽比 3.8 3.7 3.5 3.4 3.8 4.0 3.6 4.0 3.6 4.0
荔枝树叶的长宽比 2.0 2.0 2.0 2.4 1.8 1.9 1.8 2.0 1.3 1.9
【实践探究】分析数据如下:
平均数 中位数 众数 方差
芒果树叶的长宽比 3.74 m 4.0 0.0424
荔枝树叶的长宽比 1.91 1.95 n 0.0669
【问题解决】
(1)上述表格中:_________,_________.
(2)①A同学说:“从树叶的长宽比的方差来看,我认为芒果树叶的形状差别大.”
②B同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的两倍.”
上面两位同学的说法中,合理的是_____________(填序号).
(3)现有一片长,宽的树叶,请判断这片树叶更可能来自芒果、荔枝中的哪种树,并给出你的理由.
21.(12分)为进一步宣传防溺水知识,提高学生防溺水的能力,某校组织七、八年级各200名学生进行防溺水知识竞赛(满分100分).现分别在七、八年级中各随机抽取10名学生的测试成绩x(单位:分)进行统计、整理如下:
七年级:86,90,79,84,74,93,76,81,90,87.
八年级:85,76,90,81,84,92,81,84,83,84.
七、八年级测试成绩频数统计表
七年级 3 4 3
八年级 1 7 a
七、八年级测试成绩分析统计表
平均数 中位数 众数 方差
七年级 84 b 90 36.4
八年级 84 84 c 18.4
根据以上信息,解答下列问题:
(1)___________,__________,__________;
(2)按学生的实际成绩,你认为哪个年级的学生掌握防溺水知识的总体水平较好 请说明理由.
(3)如果把的记为“优秀”,把的记为“合格”,学校规定两项成绩按6:4计算,通过计算比较哪个年级得分较高
答案以及解析
1.答案:C
解析:由于丙的方差较小,平均数较大,则应推荐丙.
故选:C.
2.答案:B
解析:一组数据为4,2,a,5,1,这组数据的平均数为3,
这组数据之和为:,
,
故选:B.
3.答案:C
解析:把投中的次数按从小到大排列6,6,7,7,8,8,8,9,处于中间的两个数是7与8,7与8的平均数为7.5,所以投中次数的中位数为7.5;
因为众数是出现频数最高的数据,投中次数是8次的人数有3人,最多,故投中次数的众数是8.
故选:C.
4.答案:C
解析:由统计图可知,前三次的中位数是8,
第四次买的水蜜桃单价是a元/千克,这四个单价的中位数恰好也是众数,
,
故选C.
5.答案:C
解析:这组数据有唯一的众数3,
,
将数据从小到大排列为:0,1,2,2,3,3,3,
则平均数,
中位数为:2.
故选:C.
6.答案:D
解析:这组数据的平均数是:;
-1出现了2次,出现的次数最多,则众数是-1;
把这组数据从小到大排列为:-1,-1,2,4,最中间的数是第2、3个数的平均数,则中位数是;
这组数据的方差是:;
故选D.
7.答案:A
解析:小明的总评成绩是:
(分).
故选:A.
8.答案:D
解析:A.甲的数学成绩高于班级平均分,且成绩比较稳定,故A选项正确;
B.乙的数学成绩在班级平均分附近波动,且比丙好,故B选项正确;
C.丙的数学成绩低于班级平均分,但成绩逐次提高,故C选项正确;
D.就甲、乙、丙三个人而言,丙的数学成绩最不稳定,故D选项错误.
9.答案:B
解析:中位数与8有关,且添加一个数据a后这组新数据的中位数恰好也是众数,
这组新数据的中位数和众数都是8,
,.故选B.
10.答案:D
解析:由图中数据可知小于14的4人,大于14的也是4人,
这组数据的中位数为14,
队员年龄的唯一的众数与中位数相等,
众数是14,即年龄为14的人最多,
14岁的队员最少有4人.
这个轮滑队队员人数m最小值,
故选:D.
11.答案:8环
解析:这运动员所得环数的平均数为环,
故答案为:8环.
12.答案:甲
解析:因为,
方差小的为甲,
所以甲、乙两名同学投掷实心球成绩比较稳定的是甲.
故答案为:甲.
13.答案:6
解析:因为这组数据共有6个数,
所以将其按从小到大进行排序后,第3个数和第4个数的平均数即为中位数,
又因为这组数据的中位数为5,
所以第3个数和第4个数的和为,
所以只能是,
解得,
故答案为:6.
14.答案:4
解析:由题意知,,
解得,
这组数据为1,2,3,5,5,8,
这组数据的中位数是,
故答案为:4.
15.答案:2.8
解析:因为这组数据4,a,5,3,8的平均数为a,所以,解得,故这组数据的方差.
16.答案:(1)85,70,85,100
(2)初中部的成绩更好,理由见解析
解析:(1)根据统计图可得初中部5位选手的成绩从小到大排列为:75,80,85,85,100
高中部5位选手的成绩从小到大排列为:70,75,80,100,100
故初中部的中位数为:85(分);
方差为;
高中部的平均数为(分);
众数为100(分);
故填表如下:
平均数(分) 中位数(分) 众数(分) 方差
初中部 85 85 85 70
高中部 85 80 100 160
故答案为:85,70,85,100.
(2)答:我觉得初中部的成绩更好,因为初中部和高中部的成绩平均数一样,但是初中部的方差比高中部小,成绩更整齐.
17.答案:(1)30元,30元;
(2)32.4元;
(3)35640元;
解析:(1)根据统计图可知金额为30元的有20名学生为最多,即可知众数为30元.
根据统计图可知按金额从小到大排列,50名学生中,第25和26名学生的金额都为30元,即可知中位数为30元.
故答案为30元,30元;
(2)(元)
故该班同学所抢红包的平均金额是32.4元;
(3)(元)
故该校学生春节期间所抢的红包总金额约为35640元.
18.答案:(1)数学平均分是(分),中位数为70分;
英语平均分是(分),
中位数为85分.故答案为70,70,85,85.
(2)数学成绩的方差为,
英语成绩的方差为.
A同学数学标准分为,
A同学英语标准分为,
因为,
所以A同学在本次考试中,数学学科考得更好.
19.
解析:(1)
(2)抽取员工总数为:(人)
每人所创年利润的众数是8万元,
平均数是:万元
(3)(人)
答:在公司1200员工中有384人可以评为优秀员工.
20.(1)答案:3.75;2.0
解析:把芒果树叶的长宽比按照从小到大的顺序排列为3.4,3.5,3.6,3.6,3.7,3.8,3.8,4.0,4.0,4.0,第5,6位的数分别为3.7,3.8,
中位数为,;
荔枝树叶的长宽比数据中,2.0出现了4次,出现的次数最多,
众数是2.0,.
(2)答案:②
解析:从树叶的长宽比的方差来看,芒果树叶的长宽比的方差较小,所以芒果树叶的形状差别较小;从树叶的长宽比的平均数、中位数和众数来看,荔枝树叶的长约为宽的两倍.
(3)答案:这片树叶更可能来自荔枝树.理由见解析
解析:这片树叶更可能来自荔枝树.理由如下:
,
结合两种树叶的长宽比的平均数、中位数和众数,可知这片树叶更可能来自荔枝树.
21.答案:(1)2,85,84;
(2)八年级,理由见解析;
(3)七年级得分较高;
解析:(1),
根据众数的定义可知,,
把七年级10名学生的测试成绩按从小到大的顺序排
列为74,76,79,81,84,86,87,90,90,93,
根据中位数的定义可知,该组数据的中位数为,故.
(2)八年级学生掌握防溺水知识的总体水平较好,理由:七、八年级成绩的平均数相等,但八年级成绩的方差小于七年级成绩的方差,所以八年级学生掌握防溺水知识的总体水平较好.
(3)七年级得分:,
八年级得分:,
因为,所以七年级得分较高.
2
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
