2.10 科学记数法 课件(27张PPT)
文档属性
| 名称 | 2.10 科学记数法 课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
北师大版 数学 七年级上册
10 科学记数法
第二章 有理数及其运算
学习目标
1.能用科学记数法表示大数,会把用科学记数法表示的大数还原成原数.(重点)
2.归纳出科学记数法中指数与整数位数之间的关系.(难点)
1.回顾有理数的乘方运算,算一算:
(1) 102= ,104= ,108= .
(2)(-10)21表示 .
一、导入新课
100
10 000
100 000 000
21个-10相乘
复习回顾
2.正数的任何次幂都是 ;负数的奇次幂是 ,负数的偶次幂是 .
正数
负数
正数
一、导入新课
第七次全国人口普查时,我国全国总人口约为
1 440 000 000人.
地球半径约为
6 400 000 米.
光的速度约为
300 000 000 米.
情境导入
在生活中我们经常会见到一些很大的数,例如:
这些大数有简单的表示方法吗?
计算下列各式:
101=___, 102=____,103=_____,104=_______,
105=_________,1010=_____________,….
探究:科学计数法
二、新知探究
10
100
1000
10000
100000
10000000000
(1)指数与运算结果中的0的个数有什么关系?
(2)指数与运算结果的数位有什么关系?
讨论:
10 102 103 104 105 … 10n
指数 …
运算结果中0的个数 …
运算结果的位数 …
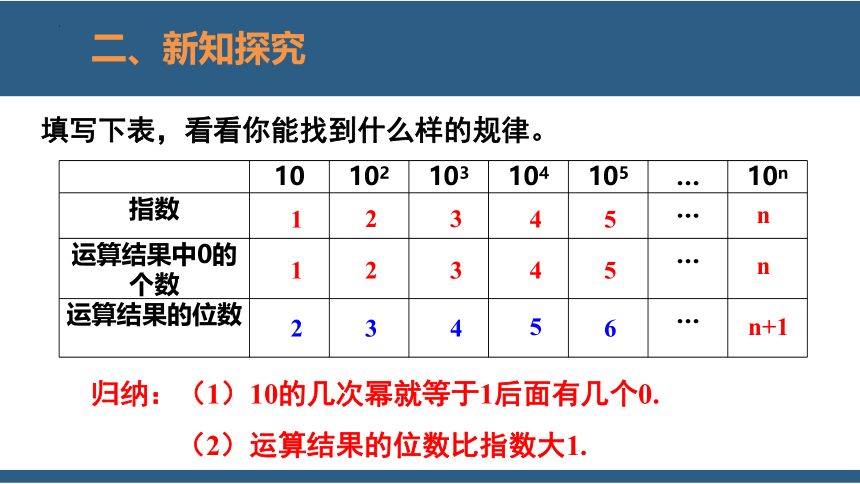
二、新知探究
1
2
3
4
5
2
1
3
4
5
6
5
4
3
2
填写下表,看看你能找到什么样的规律。
归纳:(1)10的几次幂就等于1后面有几个0.
(2)运算结果的位数比指数大1.
n
n
n+1
二、新知探究
反之,1后面有多少个0,10的幂指数就是多少.
知识归纳
二、新知探究
(1) 400 000
= 4 × 100 000
= 4 × 105
400 000
400 000 = 4 × 105
小数点原来的位置
小数点最后的位置
小数点向左移了5次
试一试:你能不能借助以10为底的幂来表示下列各数呢?
二、新知探究
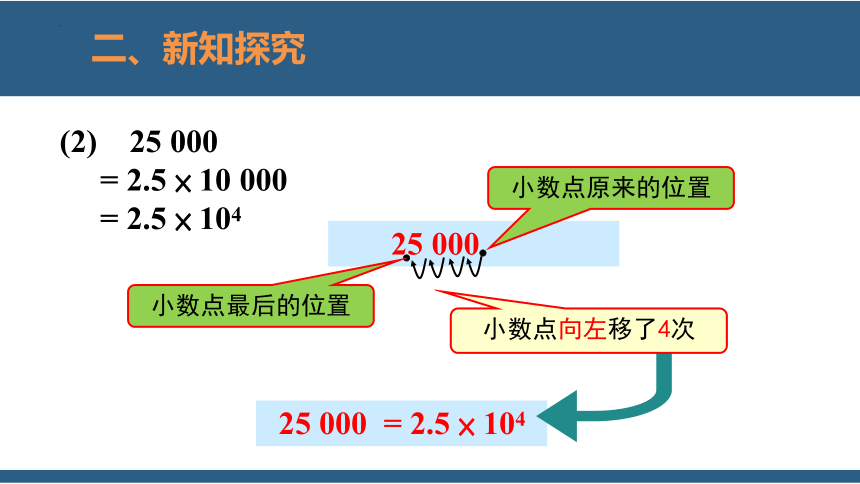
(2) 25 000
= 2.5 × 10 000
= 2.5 × 104
25 000
25 000 = 2.5 × 104
小数点原来的位置
小数点最后的位置
小数点向左移了4次
二、新知探究
(3) 5 034
= 5.034 × 1 000
= 5.034 × 103
5 034
5 034 = 5.034 × 103
小数点原来的位置
小数点最后的位置
小数点向左移了3次
二、新知探究
10的指数=整数位数-1
观察与思考:上面的式子中,等号左边整数的位数与右边10的指数有什么关系?
(2)25 000= 2.5 × 104
(1)400 000= 4 × 105
(3)5 034= 5.034 × 103
由上可知,我们可以借助10的幂的形式表示大数.
1 440 000 000可以表示成 ;
6 400 000可以表示成 ;
300 000 000可以表示成 .
二、新知探究
1.44×109
6.4×106
3×108
二、新知探究
210 000 000=2.1×108
8+1位
科学记数法中 10的指数n值的确定法:
①比原整数位数少1(当原数的绝对值≥10时);
②由小数点的移动位数来确定.
指数为8
一般地,一个大于10的数可以表示成a×10n的形式,其中1≤a<10,n是正整数,这种记数方法叫做科学记数法.
知识归纳
用科学记数法表示下列各数:
(1) 1 000 000 = ;(2) 57 000 000 = ;
(3)696 000= ;(4) 300 000 000= ;
(5)-78 000= ;(6) -12 000 000 000 = .
跟踪练习1
二、新知探究
1×106
5.7×107
6.96×105
3×108
-7.8×104
-1.2×1010
归纳:(1)用科学记数法表示一个数,只会改变这个数的书写形式,不会改变它的大小.
(2)小于-10的数也可以用科学记数法表示,只是多一个负号,记作-a×10n.
下列各数的书写形式是否是科学记数法的形式?
(1)1.5×103; (2)29×104;(3)0.32×103; (4)2.23×100.
议一议
二、新知探究
解:(1)是;
(2)不是,因为29>10;
(3)不是,因为0.32<1;
(4)不是,因为100不是10n的形式.
请你把下列数据用科学记数法表示出来.
(1)赤道长度约为40 000 000m: m;
(2)地球表面积约为510 000 000 km2: km2;
(3)人的大脑约有 10 000 000 000 个细胞: 个;
(4)森林面积约为128 630 000 公项: 公顷;
(5)某年某省的地区生产总值达到6030 亿元: 元.
跟踪练习2
二、新知探究
1×1010
4×107
1.2863×108
6.03×1011
注意:把含有计数单位(如万、亿等)的数用科学记数法表示时,先把计数单位化去,再用科学记数法表示.
5.1×108
下列用科学记数法表示的数的原数是什么
(1) 3.8×105= ;(2) 5.007×107= ;
(3) 5.940 6×102= ;(4)-7.0010×103= .
做一做
380000
50070000
594.06
-7001
二、新知探究
归纳:a×10n的原数的整数位数为n+1,原数等于把a的小数点向右移动n位所得的数,若向右移动时位数不够,则用0补上.注意符号.
例1:(1)预计到2025年我国高铁运营里程将达到38000千米.将数据38000用科学记数法表示为 .
(2)习总书记指出,善于学习,就是善于进步.“学习强国”平台上线后的某天,全国大约有1.2亿人在平台上学习.1.2亿这个数用科学记数法表示为 .
三、典例精析
3.8×104
1.2×108
三、典例精析
例2:写出下列用科学记数法表示的数的原数.
(1)地球绕太阳公转的速度约是1.1×105千米/时:___________;
(2)一个正常人一年的心跳次数大约为3.679×107次:________.
110000
36790000
三、典例精析
例3:省希望工程办公室收到社会各界人士捐款共1500万元,以此来资助贫困失学儿童.
(1)如果每名失学儿童可获得500元的资助,那么共可资助多少名失学儿童?用科学记数法表示结果;
(2)如果社会各界人士的捐款数平均为10元/人,那么要多少人捐款才能获得这笔捐款?用科学记数法表示结果.
解:1500万元=15000000元,
(1)15000000÷500=30000=3×104(名).
因此,共可资助3×104名失学儿童.
(2)15000000÷10=1500000=1.5×106(人).
因此,需要1.5×106人捐款才能获得这笔捐款.
1.下面属于科学记数法的是( )
A.25×103
B.0.3×105
C.300×10
D.5.4×107
四、当堂练习
D
2. 用科学记数法表示3080000,正确的是( )
A. 308×104 B. 30.8 ×105 C. 3.08 ×106 D. 3.8 ×106
C
3.天文单位是天文学中计量天体之间距离的一种单位,其数值取地球与太阳之间的平均距离,即149597870700 m,约为149600000 km.将数149600000用科学记数法表示为( )
A.14.96×107 B.1.496×107 C.14.96×108 D.1.496×108
D
四、当堂练习
6.一个整数815550…0用科学记数法表示为8.1555×1010,则原数中“0”的个数为( )A.5 B.6 C.7 D.8
B
4.节约是一种美德,节约是一种智慧.据不完全统计,全国每年浪费食物总量折合粮食可养活约3亿5千万人.3亿5千万用科学记数法表示为( )
A.3.5×107 B.3.5×108 C.3.5×109 D.3.5×1010
B
5.下列求原数不正确的是( )
A.3.56×104=35 600 B.-4.67×106=-4 670 000
C.2×102=200 D.3×105=30 000
D
四、当堂练习
7.用科学记数法表示下列横线上的数:
(1)我国陆地领土面积大约为9600000 km2.__________;
(2)全球每小时约有5100000 t污水排入江河湖海.__________;
(3)1光年大约等于9.46万亿千米.__________.
9.6×106
5.1×106
9.46×1012
四、当堂练习
8.写出下列用科学记数法表示的数的原数:
(1)全世界的人口大约有7.3×109人;
(2)长城长约2.12×104千米;
(3)月亮和地球的距离大约是3.84×105千米.
解:(1)7.3×109=7300000000.
(2)2.12×104=21200.
(3)3.84×105=384000.
四、当堂练习
9.已知光的传播速度为300000000 m/s,太阳光到达地球的时间大约是500 s,试计算太阳与地球的距离大约是多少千米.(结果用科学记数法表示)
解:光的速度可表示为3×108 m/s.
由题意,得3×108×500=1500×108=1.5×1011(m)=1.5×108 (km).
因此,太阳与地球的距离大约是1.5×108 km.
五、课堂小结
用科学记数法表示的大数还原成原数
定义
科学记数法
用科学记数法表示大数
一般地,一个大于10的数可以表示成a×10n的形式,其中1≤a<10,n是正整数,这种记数方法叫做科学记数法.
科学记数法中10的指数n值的确定法:①比原整数位数少1(当原数的绝对值≥10时);②由小数点的移动位数来确定.
a×10n的原数的整数位数为n+1,原数等于把a的小数点向右移动n位所得的数,若向右移动时位数不够,则用0补上.注意符号.
六、作业布置
习题2.15
北师大版 数学 七年级上册
10 科学记数法
第二章 有理数及其运算
学习目标
1.能用科学记数法表示大数,会把用科学记数法表示的大数还原成原数.(重点)
2.归纳出科学记数法中指数与整数位数之间的关系.(难点)
1.回顾有理数的乘方运算,算一算:
(1) 102= ,104= ,108= .
(2)(-10)21表示 .
一、导入新课
100
10 000
100 000 000
21个-10相乘
复习回顾
2.正数的任何次幂都是 ;负数的奇次幂是 ,负数的偶次幂是 .
正数
负数
正数
一、导入新课
第七次全国人口普查时,我国全国总人口约为
1 440 000 000人.
地球半径约为
6 400 000 米.
光的速度约为
300 000 000 米.
情境导入
在生活中我们经常会见到一些很大的数,例如:
这些大数有简单的表示方法吗?
计算下列各式:
101=___, 102=____,103=_____,104=_______,
105=_________,1010=_____________,….
探究:科学计数法
二、新知探究
10
100
1000
10000
100000
10000000000
(1)指数与运算结果中的0的个数有什么关系?
(2)指数与运算结果的数位有什么关系?
讨论:
10 102 103 104 105 … 10n
指数 …
运算结果中0的个数 …
运算结果的位数 …
二、新知探究
1
2
3
4
5
2
1
3
4
5
6
5
4
3
2
填写下表,看看你能找到什么样的规律。
归纳:(1)10的几次幂就等于1后面有几个0.
(2)运算结果的位数比指数大1.
n
n
n+1
二、新知探究
反之,1后面有多少个0,10的幂指数就是多少.
知识归纳
二、新知探究
(1) 400 000
= 4 × 100 000
= 4 × 105
400 000
400 000 = 4 × 105
小数点原来的位置
小数点最后的位置
小数点向左移了5次
试一试:你能不能借助以10为底的幂来表示下列各数呢?
二、新知探究
(2) 25 000
= 2.5 × 10 000
= 2.5 × 104
25 000
25 000 = 2.5 × 104
小数点原来的位置
小数点最后的位置
小数点向左移了4次
二、新知探究
(3) 5 034
= 5.034 × 1 000
= 5.034 × 103
5 034
5 034 = 5.034 × 103
小数点原来的位置
小数点最后的位置
小数点向左移了3次
二、新知探究
10的指数=整数位数-1
观察与思考:上面的式子中,等号左边整数的位数与右边10的指数有什么关系?
(2)25 000= 2.5 × 104
(1)400 000= 4 × 105
(3)5 034= 5.034 × 103
由上可知,我们可以借助10的幂的形式表示大数.
1 440 000 000可以表示成 ;
6 400 000可以表示成 ;
300 000 000可以表示成 .
二、新知探究
1.44×109
6.4×106
3×108
二、新知探究
210 000 000=2.1×108
8+1位
科学记数法中 10的指数n值的确定法:
①比原整数位数少1(当原数的绝对值≥10时);
②由小数点的移动位数来确定.
指数为8
一般地,一个大于10的数可以表示成a×10n的形式,其中1≤a<10,n是正整数,这种记数方法叫做科学记数法.
知识归纳
用科学记数法表示下列各数:
(1) 1 000 000 = ;(2) 57 000 000 = ;
(3)696 000= ;(4) 300 000 000= ;
(5)-78 000= ;(6) -12 000 000 000 = .
跟踪练习1
二、新知探究
1×106
5.7×107
6.96×105
3×108
-7.8×104
-1.2×1010
归纳:(1)用科学记数法表示一个数,只会改变这个数的书写形式,不会改变它的大小.
(2)小于-10的数也可以用科学记数法表示,只是多一个负号,记作-a×10n.
下列各数的书写形式是否是科学记数法的形式?
(1)1.5×103; (2)29×104;(3)0.32×103; (4)2.23×100.
议一议
二、新知探究
解:(1)是;
(2)不是,因为29>10;
(3)不是,因为0.32<1;
(4)不是,因为100不是10n的形式.
请你把下列数据用科学记数法表示出来.
(1)赤道长度约为40 000 000m: m;
(2)地球表面积约为510 000 000 km2: km2;
(3)人的大脑约有 10 000 000 000 个细胞: 个;
(4)森林面积约为128 630 000 公项: 公顷;
(5)某年某省的地区生产总值达到6030 亿元: 元.
跟踪练习2
二、新知探究
1×1010
4×107
1.2863×108
6.03×1011
注意:把含有计数单位(如万、亿等)的数用科学记数法表示时,先把计数单位化去,再用科学记数法表示.
5.1×108
下列用科学记数法表示的数的原数是什么
(1) 3.8×105= ;(2) 5.007×107= ;
(3) 5.940 6×102= ;(4)-7.0010×103= .
做一做
380000
50070000
594.06
-7001
二、新知探究
归纳:a×10n的原数的整数位数为n+1,原数等于把a的小数点向右移动n位所得的数,若向右移动时位数不够,则用0补上.注意符号.
例1:(1)预计到2025年我国高铁运营里程将达到38000千米.将数据38000用科学记数法表示为 .
(2)习总书记指出,善于学习,就是善于进步.“学习强国”平台上线后的某天,全国大约有1.2亿人在平台上学习.1.2亿这个数用科学记数法表示为 .
三、典例精析
3.8×104
1.2×108
三、典例精析
例2:写出下列用科学记数法表示的数的原数.
(1)地球绕太阳公转的速度约是1.1×105千米/时:___________;
(2)一个正常人一年的心跳次数大约为3.679×107次:________.
110000
36790000
三、典例精析
例3:省希望工程办公室收到社会各界人士捐款共1500万元,以此来资助贫困失学儿童.
(1)如果每名失学儿童可获得500元的资助,那么共可资助多少名失学儿童?用科学记数法表示结果;
(2)如果社会各界人士的捐款数平均为10元/人,那么要多少人捐款才能获得这笔捐款?用科学记数法表示结果.
解:1500万元=15000000元,
(1)15000000÷500=30000=3×104(名).
因此,共可资助3×104名失学儿童.
(2)15000000÷10=1500000=1.5×106(人).
因此,需要1.5×106人捐款才能获得这笔捐款.
1.下面属于科学记数法的是( )
A.25×103
B.0.3×105
C.300×10
D.5.4×107
四、当堂练习
D
2. 用科学记数法表示3080000,正确的是( )
A. 308×104 B. 30.8 ×105 C. 3.08 ×106 D. 3.8 ×106
C
3.天文单位是天文学中计量天体之间距离的一种单位,其数值取地球与太阳之间的平均距离,即149597870700 m,约为149600000 km.将数149600000用科学记数法表示为( )
A.14.96×107 B.1.496×107 C.14.96×108 D.1.496×108
D
四、当堂练习
6.一个整数815550…0用科学记数法表示为8.1555×1010,则原数中“0”的个数为( )A.5 B.6 C.7 D.8
B
4.节约是一种美德,节约是一种智慧.据不完全统计,全国每年浪费食物总量折合粮食可养活约3亿5千万人.3亿5千万用科学记数法表示为( )
A.3.5×107 B.3.5×108 C.3.5×109 D.3.5×1010
B
5.下列求原数不正确的是( )
A.3.56×104=35 600 B.-4.67×106=-4 670 000
C.2×102=200 D.3×105=30 000
D
四、当堂练习
7.用科学记数法表示下列横线上的数:
(1)我国陆地领土面积大约为9600000 km2.__________;
(2)全球每小时约有5100000 t污水排入江河湖海.__________;
(3)1光年大约等于9.46万亿千米.__________.
9.6×106
5.1×106
9.46×1012
四、当堂练习
8.写出下列用科学记数法表示的数的原数:
(1)全世界的人口大约有7.3×109人;
(2)长城长约2.12×104千米;
(3)月亮和地球的距离大约是3.84×105千米.
解:(1)7.3×109=7300000000.
(2)2.12×104=21200.
(3)3.84×105=384000.
四、当堂练习
9.已知光的传播速度为300000000 m/s,太阳光到达地球的时间大约是500 s,试计算太阳与地球的距离大约是多少千米.(结果用科学记数法表示)
解:光的速度可表示为3×108 m/s.
由题意,得3×108×500=1500×108=1.5×1011(m)=1.5×108 (km).
因此,太阳与地球的距离大约是1.5×108 km.
五、课堂小结
用科学记数法表示的大数还原成原数
定义
科学记数法
用科学记数法表示大数
一般地,一个大于10的数可以表示成a×10n的形式,其中1≤a<10,n是正整数,这种记数方法叫做科学记数法.
科学记数法中10的指数n值的确定法:①比原整数位数少1(当原数的绝对值≥10时);②由小数点的移动位数来确定.
a×10n的原数的整数位数为n+1,原数等于把a的小数点向右移动n位所得的数,若向右移动时位数不够,则用0补上.注意符号.
六、作业布置
习题2.15
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
