2.2.1整式的加减第1课时合并同类项 课件(23张PPT)
文档属性
| 名称 | 2.2.1整式的加减第1课时合并同类项 课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 14:36:01 | ||
图片预览








文档简介
(共23张PPT)
第2章
整式
2.2.1整式的加减
第1课时合并同类型
教学目标/Teaching aims
1
2
3
1.银行职员数钞票时,把100元票面、50元票面、20元票面、10元票面…的人民币分类来数,在多项式中是否也有类似的情形呢?
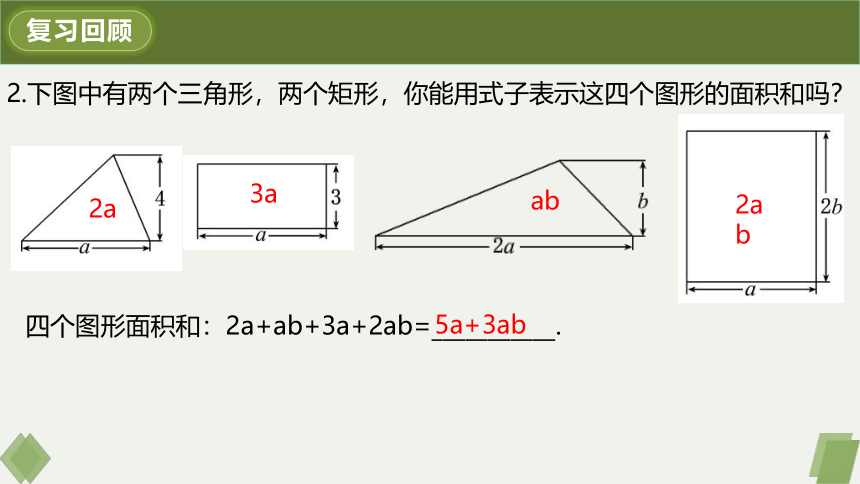
2.下图中有两个三角形,两个矩形,你能用式子表示这四个图形的面积和吗?
四个图形面积和:2a+ab+3a+2ab=___________.
2a
3a
ab
2ab
5a+3ab
7n
-8a2b
4ab2
2a2b
6xy
3n
-5xy
-2ab2
有八只小青蛙,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小青蛙分到不同的房间里吗?(无论你用几个房间)
运用运算律计算:
100×2+252×2= ;
100×(– 2)+252×(– 2)= .
100×2+252×2
100×(– 2)+252×(– 2)
= (100+252)×2
= 704
= (100+252)×(– 2)
= – 704
= 352×2
= 352×(– 2)
(100+252)×2= 352×2
(100+252)×(– 2)= 352×(– 2)
100t+252t
= (100+252)t
分配律
填空:
分配律
都有t
都有x2
都有ab2
多项式中的每一项都含有相同字母
相同字母的指数相同
所含字母相同,并且相同字母的指数也相同的单项式叫做同类项.
同类项的定义:
x+y和xy 是同类项吗
2.所含的字母相同
3.相同字母的指数也相同
同类项
1.都是单项式
3和-4是同类项吗?
×
×
×
特别规定:
所有的常数项也看做同类项.
ab和abc 是同类项吗
a2b和ab2 是同类项吗
同类项
与所含字母的顺序无关
与系数大小无关
1. 两相同:字母相同,相同字母指数相同.
2. 两无关:与系数无关,与字母顺序无关.
3. 常数项都是同类项.
同类项的判别方法
1.下列各组中的单项式是不是同类项?
注意:几个常数项也是同类项
×
√
√
√
×
×
抓住两同 两无关
2.找出下列单项式中的同类项
在多项式中遇到同类项,可以运用交换律,结合律,分配律进行合并.
例如:4x2+2x+7+3x-8x2-2
= (4x2-8x2)+(2x+3x)+(7-2)
=(4-8)x2+(2+3)x+(7-2)
= -4x2+5x+5
分配律
交换律
结合律
把多项式中的同类项合并成一项,叫做合并同类项.
定义:
法则:
(1)系数:系数相加;
(2)字母:字母和字母的指数不变.
例1.计算:
(1)(2a-3b)+(5a+4b);(2)(8a-7b)-(4a-5b)
解: (1)(2a-3b)+(5a+4b)
=2a-3b+5a+4b
=7a+b
去括号
合并同类项
=8a-7b-4a+5b
=4a-2b
(2)(8a-7b)-(4a-5b)
去括号
合并同类项
两无关
与所含字母的顺序无关
与系数无关
同类项
两同
相同字母的指数相同
所含字母相同
合并同类项
“一加两不变”
1.合并下列各式的同类项:
(1)4a2 + 3b2 +2ab-4a2 -4b2.
(2)-3x2y+2x2y+3xy2 - 2xy2;
解:(1) 4a2 + 3b2 +2ab-4a2 -4b2
= (4a2-4a2) + ( 3b2 -4b2) + 2ab
= (4-4)a2 + (3-4)b2 + 2ab
=-b2 + 2ab.
找
移
并
用不同的标记把同类项标出来!
加法交换律
加法结合律
(2) -3x2y+2x2y+3xy2 - 2xy2
=(-3+2)x2y+(3-2) xy2
=- x2y+xy2
2. (1) 求多项式 的值,其中
先合并同类项
再代入求值
(1)
当 时,
原式=
3.若mn=m+3,则2mn+3m-5mn+10=_____.
1
提示:2mn+3m-5mn+10=2(m+3)+3m-5(m+3)+10=1.
4.先化简再求值:4x2y-[6xy-3(4xy-2)-x2y]+1,
其中x=2,y=- .
当x=2,y=- 时,
原式=5×22×(- )+6×2×(- )-5
=-21.
解:原式=4x2y-[6xy-12xy+6-x2y]+1
=4x2y-6xy+12xy-6+x2y+1
=5x2y+6xy-5
同类项与系数无关,与字母顺序无关.
(2)并同类项的法则:______________相加,作为
结果的系数,字母和字母的指数_______.
同类项的系数
不变
步骤:一分,二移,三合并.
2.所含的字母相同
3.相同字母的指数也相同
(1)同类项的特点
1.都是单项式
2.2.1整式的加减
第1课时合并同类项
谢谢观看
整式
第2章
整式
2.2.1整式的加减
第1课时合并同类型
教学目标/Teaching aims
1
2
3
1.银行职员数钞票时,把100元票面、50元票面、20元票面、10元票面…的人民币分类来数,在多项式中是否也有类似的情形呢?
2.下图中有两个三角形,两个矩形,你能用式子表示这四个图形的面积和吗?
四个图形面积和:2a+ab+3a+2ab=___________.
2a
3a
ab
2ab
5a+3ab
7n
-8a2b
4ab2
2a2b
6xy
3n
-5xy
-2ab2
有八只小青蛙,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小青蛙分到不同的房间里吗?(无论你用几个房间)
运用运算律计算:
100×2+252×2= ;
100×(– 2)+252×(– 2)= .
100×2+252×2
100×(– 2)+252×(– 2)
= (100+252)×2
= 704
= (100+252)×(– 2)
= – 704
= 352×2
= 352×(– 2)
(100+252)×2= 352×2
(100+252)×(– 2)= 352×(– 2)
100t+252t
= (100+252)t
分配律
填空:
分配律
都有t
都有x2
都有ab2
多项式中的每一项都含有相同字母
相同字母的指数相同
所含字母相同,并且相同字母的指数也相同的单项式叫做同类项.
同类项的定义:
x+y和xy 是同类项吗
2.所含的字母相同
3.相同字母的指数也相同
同类项
1.都是单项式
3和-4是同类项吗?
×
×
×
特别规定:
所有的常数项也看做同类项.
ab和abc 是同类项吗
a2b和ab2 是同类项吗
同类项
与所含字母的顺序无关
与系数大小无关
1. 两相同:字母相同,相同字母指数相同.
2. 两无关:与系数无关,与字母顺序无关.
3. 常数项都是同类项.
同类项的判别方法
1.下列各组中的单项式是不是同类项?
注意:几个常数项也是同类项
×
√
√
√
×
×
抓住两同 两无关
2.找出下列单项式中的同类项
在多项式中遇到同类项,可以运用交换律,结合律,分配律进行合并.
例如:4x2+2x+7+3x-8x2-2
= (4x2-8x2)+(2x+3x)+(7-2)
=(4-8)x2+(2+3)x+(7-2)
= -4x2+5x+5
分配律
交换律
结合律
把多项式中的同类项合并成一项,叫做合并同类项.
定义:
法则:
(1)系数:系数相加;
(2)字母:字母和字母的指数不变.
例1.计算:
(1)(2a-3b)+(5a+4b);(2)(8a-7b)-(4a-5b)
解: (1)(2a-3b)+(5a+4b)
=2a-3b+5a+4b
=7a+b
去括号
合并同类项
=8a-7b-4a+5b
=4a-2b
(2)(8a-7b)-(4a-5b)
去括号
合并同类项
两无关
与所含字母的顺序无关
与系数无关
同类项
两同
相同字母的指数相同
所含字母相同
合并同类项
“一加两不变”
1.合并下列各式的同类项:
(1)4a2 + 3b2 +2ab-4a2 -4b2.
(2)-3x2y+2x2y+3xy2 - 2xy2;
解:(1) 4a2 + 3b2 +2ab-4a2 -4b2
= (4a2-4a2) + ( 3b2 -4b2) + 2ab
= (4-4)a2 + (3-4)b2 + 2ab
=-b2 + 2ab.
找
移
并
用不同的标记把同类项标出来!
加法交换律
加法结合律
(2) -3x2y+2x2y+3xy2 - 2xy2
=(-3+2)x2y+(3-2) xy2
=- x2y+xy2
2. (1) 求多项式 的值,其中
先合并同类项
再代入求值
(1)
当 时,
原式=
3.若mn=m+3,则2mn+3m-5mn+10=_____.
1
提示:2mn+3m-5mn+10=2(m+3)+3m-5(m+3)+10=1.
4.先化简再求值:4x2y-[6xy-3(4xy-2)-x2y]+1,
其中x=2,y=- .
当x=2,y=- 时,
原式=5×22×(- )+6×2×(- )-5
=-21.
解:原式=4x2y-[6xy-12xy+6-x2y]+1
=4x2y-6xy+12xy-6+x2y+1
=5x2y+6xy-5
同类项与系数无关,与字母顺序无关.
(2)并同类项的法则:______________相加,作为
结果的系数,字母和字母的指数_______.
同类项的系数
不变
步骤:一分,二移,三合并.
2.所含的字母相同
3.相同字母的指数也相同
(1)同类项的特点
1.都是单项式
2.2.1整式的加减
第1课时合并同类项
谢谢观看
整式
