23.3.2 相似三角形的判定 第2课时 课件(15张PPT)
文档属性
| 名称 | 23.3.2 相似三角形的判定 第2课时 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 322.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 15:24:08 | ||
图片预览


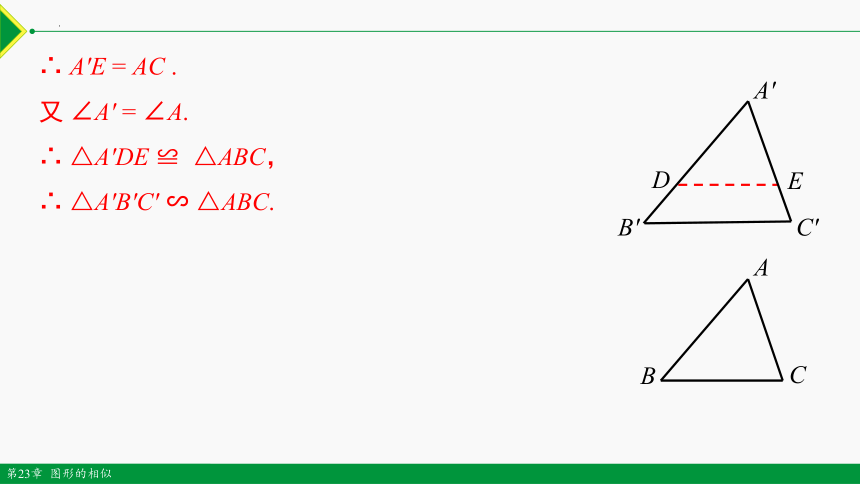

文档简介
(共15张PPT)
第23章 图形的相似
华师版(2012)九年级上册数学
两边和一夹角
三边判定两个三角形相似
| 23.3.2 相似三角形的判定 第2课时 |
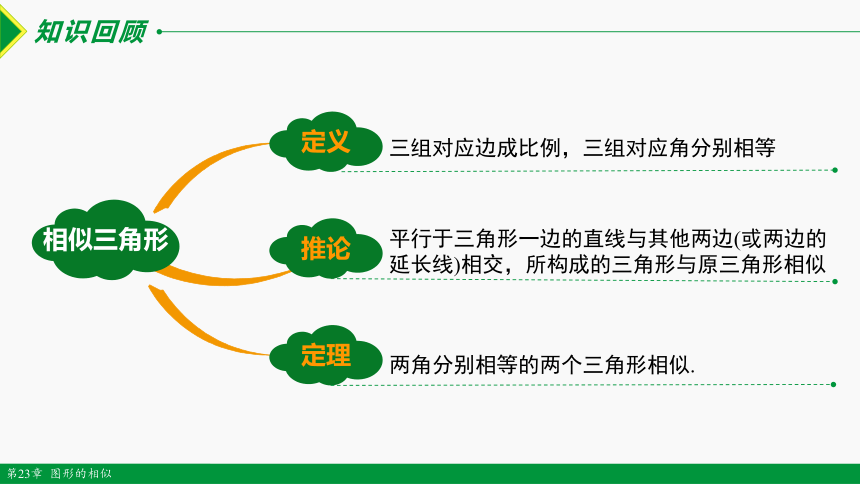
平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似
三组对应边成比例,三组对应角分别相等
知识回顾
相似三角形
定义
定理
两角分别相等的两个三角形相似.
推论
新知探究
活动一 如图,在 △ABC 与 △A′B′C′ 中,已知∠A = ∠A′
求证:△ABC∽△A′B′C′.
证明:在 △A′B′C′ 的边 A′B′ 上截取点 D,使 A′D = AB.过点 D 作 DE∥B′C′,交 A′C′ 于点 E.
B
A
C
D
E
B'
A'
C'
∵ DE∥B′C′,∴ △A′DE∽△A′B′C′.
∴
∵ A′D=AB,
∴
B
A
C
D
E
B'
A'
C'
∴ A′E = AC .
又 ∠A′ = ∠A.
∴ △A′DE ≌ △ABC,
∴ △A′B′C′ ∽ △ABC.
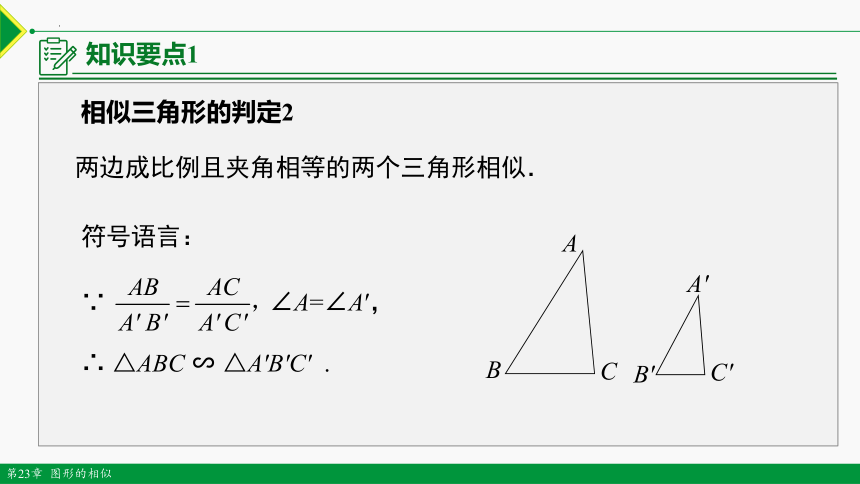
知识要点1
两边成比例且夹角相等的两个三角形相似.
相似三角形的判定2
C
A
B
A'
B'
C'
符号语言:
∵ ∠A=∠A′,
∴ △ABC ∽ △A′B′C′ .
典例讲解
例1 如图,△ABC 与△ADE 都是等腰三角形,AD = AE,AB = AC,∠DAB =∠CAE.求证:△ABC∽△ADE.
∴△ABC∽△ADE.
证明:
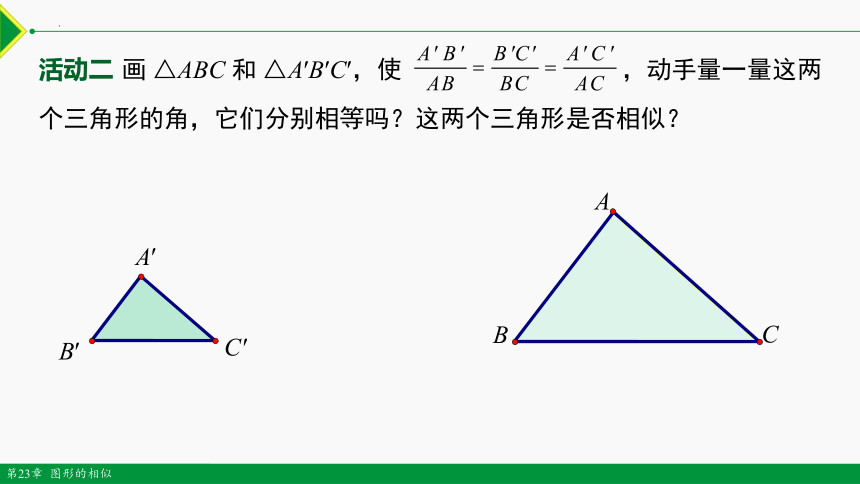
活动二 画 △ABC 和 △A′B′C′,使 ,动手量一量这两个三角形的角,它们分别相等吗?这两个三角形是否相似?
A
B
C
C′
B′
A′
证明:在线段 AB (或延长线) 上截取 AD = A′B′,过点 D 作 DE∥BC 交 AC 于点 E.
∴ DE =B′C′,EA = C′A′.
∴△ADE ≌ △A′B′C′
△A′B′C′ ∽ △ABC.
∴ , .
又 ,AD = A′B′,
∴
∵ DE∥BC ,∴ △ADE ∽ △ABC.
C′
B′
A′
B
C
A
D
E
知识要点2
三边对应成比例,两个三角形相似
相似三角形的判定3
C
A
B
A'
B'
C'
符号语言:
∴ △ABC ∽ △A′B′C′ .
典例讲解
例2
如图,已知 ,试说明∠BAD =∠CAE.
解:∵ ,
∴△ABC∽△ADE .
∴∠BAC =∠DAE .
∴∠BAC-∠DAC =∠DAE-∠DAC,
即∠BAD =∠CAE .
A
D
C
E
B
两条对应边的夹角相等
两角分别相等的两个三角形相似.
课堂小结
相似三角形
判定
判定1
判定3
三边对应成比例
判定2
课堂练习
1.根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(1)∠A = 120°,AB = 3 cm,AC = 6 cm,
∠A′ = 120°,A′B′ = 6 cm,A′C′ = 12 cm.
∴A′B′ : AB = A′C′ : AC,∠A =∠A′,
∴△A′B′C′∽△ABC
解:∵A′B′ : AB = 2,A′C′ : AC = 2,∠A =∠A′ = 120°.
(2) AB = 4 cm ,BC = 6 cm ,AC = 8 cm,
A′B′ = 12cm ,B′C′ = 18 cm ,A′C′ = 21 cm
2.如图,在四边形 ABCD 中,已知 ∠B =∠ACD,AB = 6,BC = 4,AC = 5,CD = ,求 AD 的长.
A
B
C
D
解:∵AB = 6,BC = 4,AC = 5,CD = ,
∴
又∵∠B =∠ACD,
∴ △ABC ∽ △DCA,
∴ ,
∴
3. 已知 AB = 10,BC = 8 ,AC = 16,A′B′ = 16,B′C′ = 12.8, C′A′ = 25.6,试说明△ABC∽△A′B′C′.
∴△ABC∽△A′B′C′.
第23章 图形的相似
华师版(2012)九年级上册数学
两边和一夹角
三边判定两个三角形相似
| 23.3.2 相似三角形的判定 第2课时 |
平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似
三组对应边成比例,三组对应角分别相等
知识回顾
相似三角形
定义
定理
两角分别相等的两个三角形相似.
推论
新知探究
活动一 如图,在 △ABC 与 △A′B′C′ 中,已知∠A = ∠A′
求证:△ABC∽△A′B′C′.
证明:在 △A′B′C′ 的边 A′B′ 上截取点 D,使 A′D = AB.过点 D 作 DE∥B′C′,交 A′C′ 于点 E.
B
A
C
D
E
B'
A'
C'
∵ DE∥B′C′,∴ △A′DE∽△A′B′C′.
∴
∵ A′D=AB,
∴
B
A
C
D
E
B'
A'
C'
∴ A′E = AC .
又 ∠A′ = ∠A.
∴ △A′DE ≌ △ABC,
∴ △A′B′C′ ∽ △ABC.
知识要点1
两边成比例且夹角相等的两个三角形相似.
相似三角形的判定2
C
A
B
A'
B'
C'
符号语言:
∵ ∠A=∠A′,
∴ △ABC ∽ △A′B′C′ .
典例讲解
例1 如图,△ABC 与△ADE 都是等腰三角形,AD = AE,AB = AC,∠DAB =∠CAE.求证:△ABC∽△ADE.
∴△ABC∽△ADE.
证明:
活动二 画 △ABC 和 △A′B′C′,使 ,动手量一量这两个三角形的角,它们分别相等吗?这两个三角形是否相似?
A
B
C
C′
B′
A′
证明:在线段 AB (或延长线) 上截取 AD = A′B′,过点 D 作 DE∥BC 交 AC 于点 E.
∴ DE =B′C′,EA = C′A′.
∴△ADE ≌ △A′B′C′
△A′B′C′ ∽ △ABC.
∴ , .
又 ,AD = A′B′,
∴
∵ DE∥BC ,∴ △ADE ∽ △ABC.
C′
B′
A′
B
C
A
D
E
知识要点2
三边对应成比例,两个三角形相似
相似三角形的判定3
C
A
B
A'
B'
C'
符号语言:
∴ △ABC ∽ △A′B′C′ .
典例讲解
例2
如图,已知 ,试说明∠BAD =∠CAE.
解:∵ ,
∴△ABC∽△ADE .
∴∠BAC =∠DAE .
∴∠BAC-∠DAC =∠DAE-∠DAC,
即∠BAD =∠CAE .
A
D
C
E
B
两条对应边的夹角相等
两角分别相等的两个三角形相似.
课堂小结
相似三角形
判定
判定1
判定3
三边对应成比例
判定2
课堂练习
1.根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(1)∠A = 120°,AB = 3 cm,AC = 6 cm,
∠A′ = 120°,A′B′ = 6 cm,A′C′ = 12 cm.
∴A′B′ : AB = A′C′ : AC,∠A =∠A′,
∴△A′B′C′∽△ABC
解:∵A′B′ : AB = 2,A′C′ : AC = 2,∠A =∠A′ = 120°.
(2) AB = 4 cm ,BC = 6 cm ,AC = 8 cm,
A′B′ = 12cm ,B′C′ = 18 cm ,A′C′ = 21 cm
2.如图,在四边形 ABCD 中,已知 ∠B =∠ACD,AB = 6,BC = 4,AC = 5,CD = ,求 AD 的长.
A
B
C
D
解:∵AB = 6,BC = 4,AC = 5,CD = ,
∴
又∵∠B =∠ACD,
∴ △ABC ∽ △DCA,
∴ ,
∴
3. 已知 AB = 10,BC = 8 ,AC = 16,A′B′ = 16,B′C′ = 12.8, C′A′ = 25.6,试说明△ABC∽△A′B′C′.
∴△ABC∽△A′B′C′.
